Математическая формализация задачи в декартовых координатах
Министерство образования Республики Беларусь
Министерство образования Российской Федерации
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра “Основы проектирования машин”
ВВЕДЕНИЕ В КИНЕМАТИКУ РЫЧАЖНЫХ МЕХАНИЗМОВ
МЕТОДИЧЕСКОЕ ПОСОБИЕ ПО КУРСУ ТЕОРИИ МЕХАНИЗМОВ И МАШИН
Могилев, 2007 г.
Настоящее пособие посвящено разъяснению некоторых основных положений, используемых при динамическом анализе механизмов. Прежде всего объясняется такое важнейшее понятие как сила инерции, причём подчёркивается, что её действие учитывается только в неинерциальных системах отсчёта. В рассмотренных далее примерах движение экипажа, лифта маятника, спутника объяснение даётся с двух различных точек зрения инерциального и не инерциального наблюдателя. Затем рассмотрен ряд примеров на вращательное и сложное движение твёрдых тел, являющихся элементами механизмов, а также динамическая муфта, принцип действия которой может быть понят лишь на основе динамического анализа. В заключении главы поясняется принцип Даламбера и даётся его интерпретация по отношению к механизмам.
Известно, что наибольшие трудности при решении кинематических задач в курсе ТМММ студенты технических специальностей испытывают при необходимости использования кинематической теоремы Кориолиса.
Трудности понимания ее сущности приводит к снижению интереса к изучаемому предмету. Объяснение такого положения следует искать в разрыве между объяснением теоремы Кориолиса в курсе теоретической механики и её использованием в курсе ТММ. При изложении курса теоретической механики этой теореме отводится второстепенное место, в то время как её использование в курсе ТММ занимает центральное место при кинематическом анализе механизмов. Цель настоящей методической разработки – устранить этот разрыв. Другая цель – повысить математический уровень изложения этого раздела ТММ, т.к., к сожалению, имеется большое несоответствие между общематематической подготовкой студентов и обычным способом изложения материала. Курс ТММ, как и другие общетехнические предметы, должен использовать и закреплять математические знания студентов.
|
|
|
Методическое пособие содержит пять разделов, в которых поясняется физическая сторона вопроса, затем даётся математическая формализация для случая плоского и пространственного движения, разбирается задача, относящаяся к теории пространственного манипулятора, приводятся примеры решения наиболее трудных для студентов задач из курса ТММ.
Минимально необходимые сведения могут быть почерпнуты из §1и§5,остальные разделы служат для расширения и закрепления знаний по этому вопросу и при скромном бюджете времени могут быть опущены.
|
|
|
При подготовке пособия использована следующая литература, в которой интересующийся читатель найдёт более полное изложение вопроса:
1. М.А.Айзерман. «Классическая механика». «Наука», М.,1974.
2. Е.Н.Березкин. «Курс теоретической механики», изд.МГУ,1974.
3. С.Э.Хайкин. «Физические основы механики».«Наука».М.,1971.
1. КИНЕМАТИКА СЛОЖНОГО ДВИЖЕНИЯ
Физическая модель сложного движения
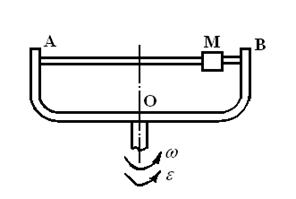
Представим следущую физическую модель: прямая штанга вращается с постоянной угловой скоростью 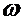 вокруг перпендикулярной к ней оси, а груз
вокруг перпендикулярной к ней оси, а груз  движется относительно штанги. (Фиг.1).
движется относительно штанги. (Фиг.1).
Следует определить скорость и ускорение т.  относительно неподвижной системы координат, т.е. абсолютную скорость и ускорение.
относительно неподвижной системы координат, т.е. абсолютную скорость и ускорение.
Фиг.1.
Очевидно, что траектория т.  в абсолютном движении представляет некоторую кривую, несовпадающую ни с окружностью, ни с радиальной прямой. (Фиг.2). Следовательно абсолютная скорость т.
в абсолютном движении представляет некоторую кривую, несовпадающую ни с окружностью, ни с радиальной прямой. (Фиг.2). Следовательно абсолютная скорость т.  как касательная к траектории направлена под каким-то непрямым углом к штанге. Разложим вектор скорости
как касательная к траектории направлена под каким-то непрямым углом к штанге. Разложим вектор скорости 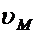 на две составляющие:
на две составляющие: 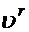 , направленную вдоль штанге, и
, направленную вдоль штанге, и 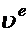 , направленную перпендикулярно к штанге. Составляющая
, направленную перпендикулярно к штанге. Составляющая 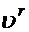 обусловлена движением т.
обусловлена движением т.  относительно штанги, составляющая
относительно штанги, составляющая 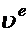 обусловлена вращением штанги и равна скорости той точки штанги, в которой в данный момент находится т.
обусловлена вращением штанги и равна скорости той точки штанги, в которой в данный момент находится т.  ,
, 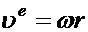 . Назовём составляющую
. Назовём составляющую 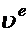 переносной скоростью, а составляющую
переносной скоростью, а составляющую 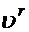 – относительной.
– относительной.
|
|
|
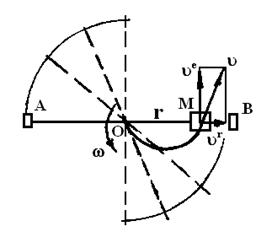
Фиг.2.
Проследим, какие изменения происходят с составляющими 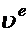 и
и 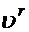 во время движения. Переносная скорость
во время движения. Переносная скорость 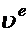 изменяется по направлению, т.к. соответствующая точка штанги движется по окружности, а также по величине. Изменение скорости, отнесённое к единице времени, представляет собой ускорение. Известно, что величина ускорения при неравномерном движении точки по окружности складывается геометрически из нормального
изменяется по направлению, т.к. соответствующая точка штанги движется по окружности, а также по величине. Изменение скорости, отнесённое к единице времени, представляет собой ускорение. Известно, что величина ускорения при неравномерном движении точки по окружности складывается геометрически из нормального 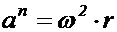 и тангенциального
и тангенциального 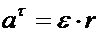 . Назовём это ускорение переносным по аналогии со скоростью и обозначим
. Назовём это ускорение переносным по аналогии со скоростью и обозначим 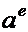 . Относительная скорость в общем случае может изменяться по величине, что обуславливает относительное ускорение
. Относительная скорость в общем случае может изменяться по величине, что обуславливает относительное ускорение 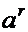 .
.
Этим, однако, не исчерпываются все возможности изменения переносной и относительной скорости. Вследствие движения т.  вдоль штанги изменяется её расстояние
вдоль штанги изменяется её расстояние 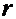 до центра вращения, а, следовательно, и величина переносной скорости. Вектор относительной скорости поворачивается вместе со штангой, т.е. изменяется по направлению. Оба эти изменения выражаются векторами, направленными перпендикулярно к штанге (Фиг.3). Изменение переносной скорости
до центра вращения, а, следовательно, и величина переносной скорости. Вектор относительной скорости поворачивается вместе со штангой, т.е. изменяется по направлению. Оба эти изменения выражаются векторами, направленными перпендикулярно к штанге (Фиг.3). Изменение переносной скорости 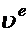 по величине происходит в направлении этой скорости, т.е. перпендикулярно штанге. Изменение направления относительной скорости
по величине происходит в направлении этой скорости, т.е. перпендикулярно штанге. Изменение направления относительной скорости 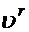 за малый промежуток времени выражается вектором, перпендикулярным вектору относительной скорости, т.е. перпендикулярно штанге. Оба эти изменения скоростей не учтены в переносном и относительном ускорениях и обуславливают некоторое добавочное ускорение. Величина добавочного ускорения указанных выше изменений относительной и переносной скорости за единицу времени.
за малый промежуток времени выражается вектором, перпендикулярным вектору относительной скорости, т.е. перпендикулярно штанге. Оба эти изменения скоростей не учтены в переносном и относительном ускорениях и обуславливают некоторое добавочное ускорение. Величина добавочного ускорения указанных выше изменений относительной и переносной скорости за единицу времени.
|
|
|
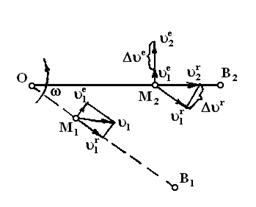
Фиг.3.
Рассмотрим два положения т.  разделённые малым промежутком времени
разделённые малым промежутком времени 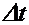 (Фиг.3). Обозначим переносную скорость в первом положении
(Фиг.3). Обозначим переносную скорость в первом положении 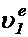 , а во втором
, а во втором 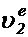 . Отложим вектор
. Отложим вектор 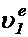 на векторе
на векторе 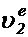 , тогда интересующее нас изменение скорости определяется так:
, тогда интересующее нас изменение скорости определяется так:
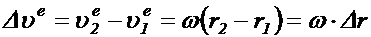 ,
,
но 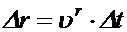 , тогда
, тогда 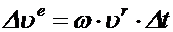 .
.
Теперь обратимся к относительной скорости. Построим рядом с вектором 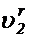 вектор
вектор 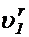 , совместив их начала. Так как
, совместив их начала. Так как 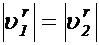 интересующее нас изменение скорости
интересующее нас изменение скорости 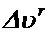 может быть найдено из образующегося здесь треугольника:
может быть найдено из образующегося здесь треугольника: 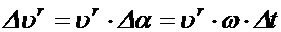 .
.
Итак, оба изменения скорости 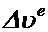 и
и 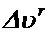 направлены в одну сторону, одинаковы по величине и определяют добавочное ускорение:
направлены в одну сторону, одинаковы по величине и определяют добавочное ускорение:
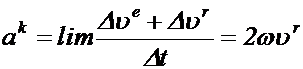 (1.1)
(1.1)
Направление добавочного ускорения зависит как от направления 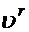 , так и от направления вращения. При изменении направления вращения на противоположное изменяется направление
, так и от направления вращения. При изменении направления вращения на противоположное изменяется направление 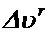 и
и 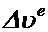 и, следовательно, изменится на противоположное направление добавочного ускорения. В этом можно убедиться, произведя построение аналогичное Фиг.3. Если относительная скорость изменит своё направление, то и
и, следовательно, изменится на противоположное направление добавочного ускорения. В этом можно убедиться, произведя построение аналогичное Фиг.3. Если относительная скорость изменит своё направление, то и 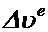 изменит направление на противоположное (т.к.
изменит направление на противоположное (т.к. 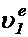 больше
больше 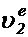 ) и
) и 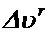 изменит направление на противоположное (т.к. поворот вектора
изменит направление на противоположное (т.к. поворот вектора 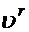 будет происходить в противоположную сторону).
будет происходить в противоположную сторону).
Математическая формализация задачи в декартовых координатах
Рассмотрим задачу об определении абсолютной скорости и ускорения для случая сложного движения с формальной, математической точки зрения. Для простоты вначале разберём задачу , когда движение происходит в одной плоскости.
Имеем две среды, неподвижную 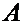 и подвижную
и подвижную 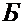 , и точку
, и точку  , которая находится в подвижной среде и движется в ней. Задача состоит в том, чтобы найти движение т.
, которая находится в подвижной среде и движется в ней. Задача состоит в том, чтобы найти движение т.  (т.
(т.  координаты, скорость и ускорение) в неподвижной среде, если известно как движется среда
координаты, скорость и ускорение) в неподвижной среде, если известно как движется среда 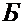 в среде
в среде 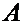 , и как движется т.
, и как движется т.  в среде
в среде 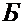 . Введём для каждой среды свою прямоугольную систему координат (Фиг.4). Обозначим интересующие нас координаты т.
. Введём для каждой среды свою прямоугольную систему координат (Фиг.4). Обозначим интересующие нас координаты т.  в неподвижной среде
в неподвижной среде 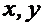 ,а известные координаты т.
,а известные координаты т.  в подвижной среде
в подвижной среде 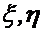 .
.
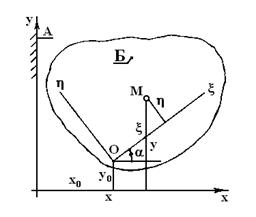
Фиг.4.
Известные из аналитической геометрии формулы преобразования координат устанавливают зависимость между координатами точки в двух системах:
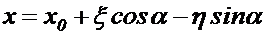 (1.2)
(1.2)
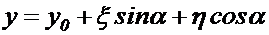 (1.3)
(1.3)
С течением времени координаты 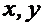 т.
т.  изменяются. Определим их скорость изменения. Известно, что математическим представлением скорости является производная по времени от функции, определяющей координату. Продифференцируем функции (1.2) и (1.3).
изменяются. Определим их скорость изменения. Известно, что математическим представлением скорости является производная по времени от функции, определяющей координату. Продифференцируем функции (1.2) и (1.3).
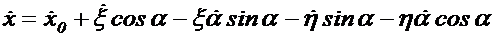 (1.4)
(1.4)
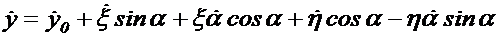 (1.5)
(1.5)
Здесь буквы с точками означают производные соответствующих параметров по времени. В формуле (1.4) выражение 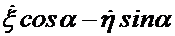 представляет проекцию вектора скорости т.
представляет проекцию вектора скорости т.  в подвижной среде
в подвижной среде 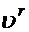
на ось 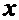 неподвижной среды. Это следует из геометрического построения на Фиг. 5.
неподвижной среды. Это следует из геометрического построения на Фиг. 5.
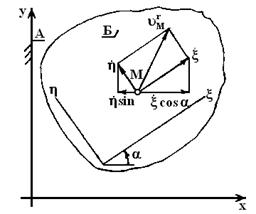
Фиг. 5.
Оставшиеся члены образуют выражение 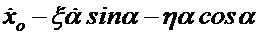 , в котором
, в котором 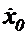 представляет проекцию на ось
представляет проекцию на ось 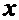 вектора скорости начала подвижной системы координат
вектора скорости начала подвижной системы координат 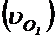 , а
, а
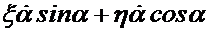 представляет проекцию на ось
представляет проекцию на ось 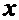 вектора скорости той точки подвижной среды
вектора скорости той точки подвижной среды 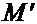 , с которой в данный момент совпадает т.
, с которой в данный момент совпадает т.  , вызванной вращением подвижной среды с угловой скоростью
, вызванной вращением подвижной среды с угловой скоростью 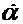 вокруг начала координат. Это следует из построения на Фиг. 6.
вокруг начала координат. Это следует из построения на Фиг. 6.
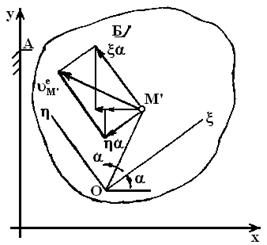
Фиг. 6.
Таким образом, структура выражения (1.4) позволяет считать, что скорость т.  в неподвижной среде складывается из двух элементов: скорости т.
в неподвижной среде складывается из двух элементов: скорости т.  относительно подвижной среды и скорости той точки подвижной среды
относительно подвижной среды и скорости той точки подвижной среды 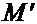 , с которой в данный момент совпадает т.
, с которой в данный момент совпадает т.  , вызванной движением среды
, вызванной движением среды 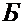 относительно
относительно 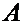 . Эти два элемента принято называть относительной скоростью и переносной скоростью.
. Эти два элемента принято называть относительной скоростью и переносной скоростью.
Итак, 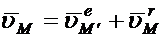 (1.6)
(1.6)
Математическим представлением ускорения является производная от функции скорость по времени. Продифференцируем функции (1.4) и (1.5):
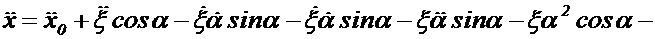
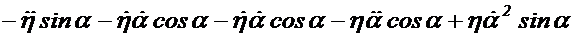 (1.7)
(1.7)
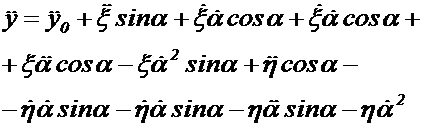 (1.8)
(1.8)
В формуле (1.7) выражение 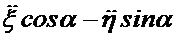 получено путем дифференцирования выражения, представляющего проекцию на ось
получено путем дифференцирования выражения, представляющего проекцию на ось 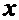 вектора относительной скорости
вектора относительной скорости 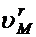 при условии
при условии 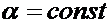 и, следовательно, по аналогии может быть названо проекцией относительного ускорения. Выражение
и, следовательно, по аналогии может быть названо проекцией относительного ускорения. Выражение 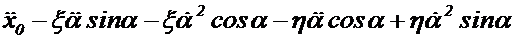
получено путем дифференцирования по времени проекции на ось 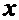 переносной скорости при условии
переносной скорости при условии 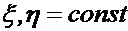 и, следовательно, может быть названо проекцией переносного ускорения. Оставшиеся числа правой части формулы (1.7) группируются в выражение
и, следовательно, может быть названо проекцией переносного ускорения. Оставшиеся числа правой части формулы (1.7) группируются в выражение 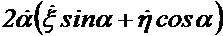 и представляют проекцию на ось
и представляют проекцию на ось 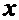 еще какого-то вектора. Этот вектор принято называть добавочным, поворотным или кориолисовым ускорением. Члены, образующие кориолисово ускорение, возникают, во-первых, в связи с дифференцированием проекции вектора относительно скорости при условии
еще какого-то вектора. Этот вектор принято называть добавочным, поворотным или кориолисовым ускорением. Члены, образующие кориолисово ускорение, возникают, во-первых, в связи с дифференцированием проекции вектора относительно скорости при условии 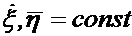 , но переменном
, но переменном 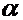 , во-вторых, при дифференцировании проекции вектора переносной скорости при условии
, во-вторых, при дифференцировании проекции вектора переносной скорости при условии 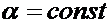 , по переменных
, по переменных 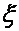 и
и 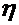 .
.
Выражение (1.7) и (1.8) в аналитической форме представляют так называемую кинематическую теорему Кориолиса, утверждающую, что абсолютное ускорение точки в сложном движении складывается геометрически из ускорения переносного, относительного и кориолисова.
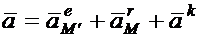 (1.9)
(1.9)
В выражении 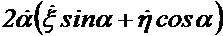 множитель
множитель 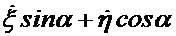 можно рассматривать как проекцию на ось
можно рассматривать как проекцию на ось 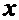 вектора относительной скорости
вектора относительной скорости 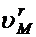 , повернутою на
, повернутою на 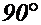 в сторону вращения подвижной среды
в сторону вращения подвижной среды 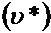 . Это следует из построения на Фиг.7.
. Это следует из построения на Фиг.7.
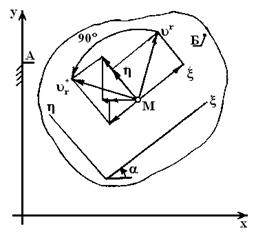
Фиг.7.
Аналогичные утверждения можно сделать для проекции добавочного ускорения на ось 
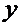 . Отсюда следует, что абсолютная величина кориолисова ускорения определяется по формуле:
. Отсюда следует, что абсолютная величина кориолисова ускорения определяется по формуле:
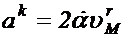 (1.10)
(1.10)
а его направление совпадает с направлением вектора относительной скорости, повернутого на 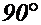 в сторону вращения подвижной среды.
в сторону вращения подвижной среды.
Заметим следующие свойства кориолисова ускорения:
1.Кориолисово ускорение отсутствует, если подвижная среда не вращается, а движется только поступательно, поскольку в этом случае 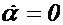 ;
;
2.Кориолисово ускорение отсутствует, если тело покоится в подвижной среде, т.к. в этом случае 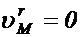 ;
;
§3.Векторная форма кинематической теоремы Кориолиса
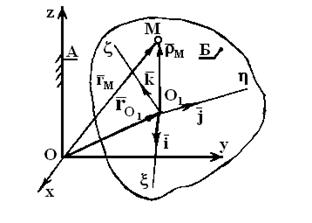
Рассмотрим задачу о сложном движении в общем случае пространственного движения. При этом воспользуемся наиболее удобным и экономным векторным способом доказательства кинематической теоремы Кориолиса. Пусть т.  находится в среде
находится в среде 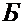 и движется относительно ее произвольным образом. Сама среда
и движется относительно ее произвольным образом. Сама среда 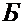 движется в пространстве относительно неподвижной среды
движется в пространстве относительно неподвижной среды 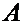 . Введем координатные системы
. Введем координатные системы 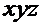 и
и 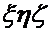 , связав их с неподвижной и подвижной средой. Пусть
, связав их с неподвижной и подвижной средой. Пусть 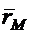 и
и 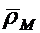 радиус-векторы т.
радиус-векторы т.  в неподвижной и подвижной среде (Фиг.8).
в неподвижной и подвижной среде (Фиг.8).
Фиг.8.
Из векторного треугольника на фиг.8 следует:
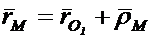 (1.11)
(1.11)
где 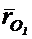 — радиус-вектор т.О. разложим радиус-вектор
— радиус-вектор т.О. разложим радиус-вектор 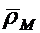 по ортам
по ортам 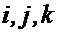 подвижной системы координат:
подвижной системы координат: 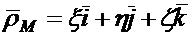 (1.12)
(1.12)
здесь 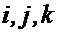 выражают проекции радиус-вектора
выражают проекции радиус-вектора 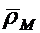 на подвижные оси. Определим скорость т.
на подвижные оси. Определим скорость т.  в неподвижной системе координат (абсолютную скорость), для чего продифференцируем выражение (1.11) с учетом (1.12) по времени:
в неподвижной системе координат (абсолютную скорость), для чего продифференцируем выражение (1.11) с учетом (1.12) по времени:
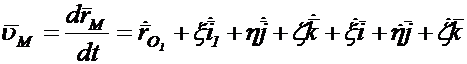 (1.13)
(1.13)
Для определения ускорения т.  в неподвижной системе продифференцируем выражение (1.13) и сгруппируем члены:
в неподвижной системе продифференцируем выражение (1.13) и сгруппируем члены:
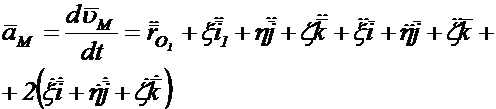 (1.14)
(1.14)
Проанализируем полученные выражения. Рассмотрим три последних члена выражения (1.13). Они совпадают с тем выражение, которое получается при разложении по осям 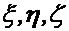 вектора скорости т.
вектора скорости т.  , если бы среда
, если бы среда 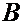 была неподвижна и, следовательно, все предыдущие члены выражения (1.13) равнялись нулю. Естественно, что в случае подвижной среды, этот вектор можно назвать относительной скоростью.
была неподвижна и, следовательно, все предыдущие члены выражения (1.13) равнялись нулю. Естественно, что в случае подвижной среды, этот вектор можно назвать относительной скоростью.
Четыре оставшихся члена совпадают с ем выражением для скорости т.  , которое получилось бы, если бы т.
, которое получилось бы, если бы т.  прекратила относительное движение в среде
прекратила относительное движение в среде 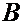 , «застряла» в ней в виде т.
, «застряла» в ней в виде т. 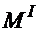 и двигалась бы только вместе со средой С. Эту скорость называют переносной. Следовательно, выражение (1.13) представляет известное соотношение:
и двигалась бы только вместе со средой С. Эту скорость называют переносной. Следовательно, выражение (1.13) представляет известное соотношение:
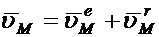 (1.15)
(1.15)
скорость т.  в неподвижной среде равна геометрической сумме скорости той точки подвижной среды
в неподвижной среде равна геометрической сумме скорости той точки подвижной среды 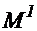 , в которой в данный момент находится т.
, в которой в данный момент находится т.  (переносной скорости) и скорости т.
(переносной скорости) и скорости т.  относительно подвижной среды (относительной скорости).
относительно подвижной среды (относительной скорости).
Первые четыре элемента выражения (1.14) 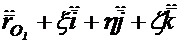 получаются путем дифференцирования выражения для переносной стороны, если считать
получаются путем дифференцирования выражения для переносной стороны, если считать 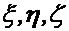 постоянными, а
постоянными, а 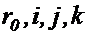 — переменными. Эти элементы составляют переносное ускорение. Следующие три элемента
— переменными. Эти элементы составляют переносное ускорение. Следующие три элемента 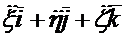 получаются при дифференцировании выражения для относительной скорости в предположении, что
получаются при дифференцировании выражения для относительной скорости в предположении, что 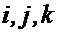 — постоянные,
— постоянные, 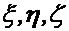 — переменные. Эти элементы составляют относительное ускорение. Наконец, последний член выражения (1.14)
— переменные. Эти элементы составляют относительное ускорение. Наконец, последний член выражения (1.14) 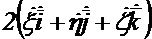 представляет сумму выражений, получаемых при дифференцировании переменной скорости в предположении, что
представляет сумму выражений, получаемых при дифференцировании переменной скорости в предположении, что 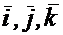 — постоянны, а
— постоянны, а 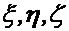 —переменные и дифференцировании относительной скорости в предположении, что
—переменные и дифференцировании относительной скорости в предположении, что 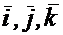 переменны, а
переменны, а 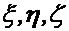 — постоянны.
— постоянны.
Таким образом, имеем:
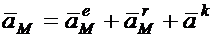 (1.16)
(1.16)
Ускорение т. М в неподвижной среде равно геометрической сумме ускорения той точки подвижной среды 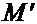 , в которой в данный момент находится т.
, в которой в данный момент находится т.  (переносное ускорение), ускорения т.
(переносное ускорение), ускорения т.  относительно подвижной среды (относительного ускорения) и дополнительного ускорения, возникающего как за счет поворота подвижной системы координат, так и относительного движения т.
относительно подвижной среды (относительного ускорения) и дополнительного ускорения, возникающего как за счет поворота подвижной системы координат, так и относительного движения т.  (кориолисово ускорение).
(кориолисово ускорение).
Выражение для кориолисова ускорения можно записать по-другому, если учесть, что изменение ортов происходит только по направлению за счет вращения подвижной среды с угловой скоростью. Можно показать, что скорости концов ортов определяются по формулам 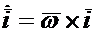 ,
, 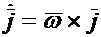 ,
,
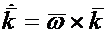 .
.
где 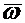 — вектор угловой скорости подвижной среды. Подставив их в выражение для кориолисова ускорения получим
— вектор угловой скорости подвижной среды. Подставив их в выражение для кориолисова ускорения получим
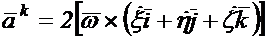 (1.16)
(1.16)
Множитель в круглых скобках представляет относительную скорость, поэтому кориолисово ускорение приводится к виду
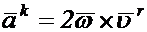 (1.17)
(1.17)
из выражения (1.17) как частные случаи следуют выражения (1.10) и (1.1). отметим, что в случае пространственного движения кориолисово ускорение отсутствует, если переносное движение является поступательным 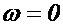 , или тело покоится в подвижной системе
, или тело покоится в подвижной системе 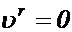 , или вектор относительной скорости (на основании свойства векторного произведения).
, или вектор относительной скорости (на основании свойства векторного произведения).
Дата добавления: 2018-05-02; просмотров: 230; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
