Индексы цен Ласпейреса, Пааше, Фишера, Лоу
Индексы цен, рассчитанные по формуле Ласпейреса, особенно широко применяются при расчете индексов потребительских цен (ИПЦ), индексов цен производителей на промышленную продукцию по данным о ценах на товары-представители. Однако данный индекс не включает инвестиционные товары, но при этом учитываются цены на импортную продукцию.
Индексы цен, рассчитанные по формуле Пааше, как правило, охватывают более широкий круг товаров и услуг. В качестве весов используется не структура потребительских расходов, а структура товарооборота, или добавленной стоимости, или произведенной продукции в текущем периоде, поэтому они могут быть определены лишь по истечении отчетного периода. Индекс цен Пааше —это индекс розничных цен, используется при измерении динамики цен компонентов ВВП, закупочных цен в сельском хозяйстве, сметных цен в строительстве, экспортных цен.
Индекс цен Ласпейреса в качестве весов использует физический объем продукции базисного периода:
 (8.5.)
(8.5.)
Этот индекс показывает, во сколько бы раз товары базисного периода подорожали (подешевели) из-за изменения цен на них в отчетном периоде при неизменной базисной структуре товаров-представителей, вошедших в потребительскую корзину.
Известно, что в индексе цен Ласпейреса весами служит продукция (потребительская корзина) в базисном периоде, и по мере отдаления от базисного года эта потребительская корзина все более, по видам, количеству и качеству вошедших в нее товаров-представителей, претерпевает изменение. Естественно, система весов должна пересматриваться при выборе базисного года, поэтому следует соблюсти критерии:
|
|
|
— базисный год должен находиться в середине длительной фазы подъема (снижения) экономического развития;
— динамика цен в базисном году не должна быть стабильной, но не должна быть и ниже, чем в соседние с ним годы;
— год должен быть «нормальным» с точки зрения различных катаклизмов.
Увязка индекса, рассчитанного по новым весам, осуществляется с помощью процедуры смыкания динамических рядов.
Индексируемой величиной виндексе цен Пааше являются цены, а весами выступает количество продукции отчетного периода.
 (8.6.)
(8.6.)
Этот индекс отвечает на вопрос: насколько товары и услуги в отчетном периоде стали дороже (дешевле), чем в базисном периоде?
Значения индексов не совпадают. Отличие значений объясняется тем, что индексы имеют разное экономическое содержание.
Индекс цен Фишера — это корень квадратный из произведения индексов цен Ласпейреса и Пааше. Экономического содержания этот индекс не имеет. Чаще всего он применяется при исчислении индексов цен за длительный период времени для сглаживания тенденций в структуре и составе объема продукции, в которых происходят значительные изменения:
|
|
|
 (8.7.)
(8.7.)
Индекс цен Фишера оценивает не только набор товаров базисного периода по ценам отчетного периода (Σq0р1), но и набор товаров отчетного периода по ценам базисного (Σq1р0). Этот индекс еще называют «идеальным» индексом, так как он является обратимым во времени.
При синтезировании общего индекса цен фактического количества товаров (в отчетный или базисный периоды) в качестве соизмерителей индексируемых величин (р1 и р0) могут применяться средние величины реализации товаров за два или большее периодов. При таком расчете формула общего индекса цен будет выглядеть следующим образом:
 (8.8.)
(8.8.)
Такой индекс называется индекс Лоу. Если при определении индекса цен исходная информация содержит лишь данные о количестве реализации товаров в базисном и текущем периодах, то средняя их величина определяется:  (8.9)
(8.9)
Индекс цен Лоу применяется при расчетах закупок или реализации товара в течении продолжительных периодов времени (пятилетках, десятилетиях и т.д.). Этот метод дает возможность анализа цен с учетом происходящих внутри отдельных субпериодов изменений в ассортиментном составе товаров.
|
|
|
Пример 1:
На основе имеющихся данных оценить изменение цен.
| товар | р0 | q0 | p1 | q1 | p0q0 | p1q1 | p0q1 | p1q0 | q cp | p0q cp | p1q cp |
| а | 15 | 10 | 17 | 15 | 150 | 255 | 225 | 170 | 12,5 | 187,5 | 212,5 |
| б | 10 | 13 | 13 | 18 | 130 | 234 | 180 | 169 | 15,5 | 155 | 201,5 |
| в | 17 | 28 | 20 | 31 | 476 | 620 | 527 | 560 | 29,5 | 501,5 | 590 |
| г | 12 | 35 | 16 | 37 | 420 | 592 | 444 | 560 | 36 | 432 | 576 |
| итого | 1176 | 1701 | 1376 | 1459 | 1276 | 1580 |
Решение:

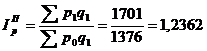


Задачи для самостоятельного решения:
Задача 53.
Имеются следующие данные о поставках продукта А:
| Страна-импортер
| Объем поставок (тыс. шт.)
| Внешнеторговая цена (долл.)
| ||
| базисный период, | отчетный период, | базисный период, | отчетный период, | |
| Болгария | 700 | 450 | 100 | 102 |
| Германия | 200 | 250 | 95 | 97 |
| Китай | 100 | 450 | 97 | 98 |
| Итого | 1000 | 1150 | — | — |
Рассчитайте: 1) среднюю цену поставок продуктаА; 2) индексы переменного состава, постоянного состава и структурных сдвигов, характеризующие динамику средней внешнеторговой цены.
|
|
|
Задача 54.
Имеются данные об объемах платных услуг образования и здравоохранения:
| Услуги
| Объем платных услуг в текущих ценах, ден. ед.
| Изменение цен, %
| |
| базисный период | отчетный период | ||
| 1. Образование | 1400 | 1600 | +10 |
| 2. Здравоохранение в том числе: а) хирургические | 700 | 700 | +14 |
| б)терапевтические | 350 | 420 | +17 |
| в)другие | 300 | 180 | +10 |
Сводный индекс цен по полному набору товаров-представителей, исчисленный по формуле цен Ласпейреса, — 0,98. Определите:
1. а) как изменились бы потребительские расходы населения на приобретение платных услуг образования и здравоохранения при неизменной структуре их потребления;
б) какие факторы оказали влияние на это изменение и в какой степени;
в) как изменилась стоимость жизни.
2. Постройте сводный индекс розничных цен на платные услуги образования и здравоохранения.
3. Сделайте выводы по каждому исчисленному показателю.
Задача 55.
Рассчитайте общее и среднее изменение цен на готовую продукцию легкой промышленности, исходя из следующих данных за 8 месяцев текущего года (в % к предыдущему месяцу):
| январь | февраль | март | апрель | май | июнь | июль | Август |
| 103,3 | 102,8 | 94,6 | 99,9 | 94,5 | 101,6 | 100,9 | 106,7 |
Задача 56.
Определите индекс товарооборота; индексы цен Ласпейреса и Пааше, если известно, что за отчетный период цена единицы изделия А выросла на 5%, изделия Б – снизилась на 5%, изделия В – выросла на 11%. Объем товарооборота в отчетном периоде по изделиям А,Б,В соответственно 780, 500, 420 ден.ед., что от товарооборота базисного периода соответственно по товарам А,Б,В составляет 1,06, 0,98, 1,17.
Задача 57.
Имеются следующие данные о реализации товаров:
| Товар | Цены, ден.ед. | Объемы реализации, тыс.шт. | ||
| 1999 | 2009 | 1999 | 2009 | |
| А | 5,2 | 25,1 | 178 | 154 |
| Б | 6,3 | 37,6 | 154 | 211 |
| В | 4,7 | 23,4 | 217 | 254 |
| Г | 8,5 | 40,2 | 386 | 394 |
Рассчитать индексы цен Ласпейреса, Пааше, Лоу. Сделайте выводы.
Задача 58.
Рассчитайте сводные индексы потребительских и розничных цен, исходя из данных по основным товарным группам:
| Товарные группы | Индекс цен за VI 2009 г. к XII 2008 г. | Удельный вес каждой товарной группы по состоянию на: | |
| XII 2008 г. | VI 2009 г. | ||
| Мясо и мясопродукты | 1,58 | 0,3717 | 0,2875 |
| Молоко и молочные продукты | 1,99 | 0,3109 | 0,2769 |
| Рыба и рыбопродукты | 1,89 | 0,0650 | 0,0646 |
| Сахар | 1,08 | 0,1631 | 0,1106 |
| Хлебные продукты | 2,34 | 0,0893 | 0,2604 |
| итого | 1,0000 | 1,0000 | |
Задача 59.
По нижеследующим данным рассчитайте индексы цен Ласпейреса, Пааше, Фишера. Проанализируйте полученные результаты.
|
| Базисный период | Отчетный период | ||
| Цена за единицу, ден.ед. | Произведено, шт. | Цена за единицу, ден.ед. | Произведено, шт. | |
| А | 450 | 2500 | 870 | 1700 |
| Б | 27 | 830 | 35 | 2300 |
| В | 12 | 610 | 14 | 4100 |
Задача 60.
Производство изделий в натуральном выражении снизилось в 1,2 раза по сравнению с прошлым годом, а стоимость продукции увеличилась в 2 раза. На сколько процентов выросли цены на данные изделия?
Вопросы для подготовки к экзамену по дисциплине «Экономическая статистика»
1. Предмет, методы и задачи экономической статистики
2. Система показателей экономической статистики
3. Общее понятие о классификациях, группировках и номенклатурах
4. Отраслевые классификации
5. Население как объект статистического изучения
6. Изучение численности населения
7. Движения населения. Перспективные расчеты численности населения.
8. Статистика занятости и безработицы
9. Показатели движения рабочей силы
10. Рабочее время. Баланс рабочего времени.
11. Использование рабочего времени.
12. Статистика оплаты труда. Состав фонда заработной платы.
13. Показатели уровня и динамики заработной платы. Дифференциация заработной платы
14. СНС (общие понятия).
15. Основные счета СНС
16. Система макроэкономических показателей. ВВ, ВДС.
17. Методы определения ВВП. Дефлятор ВВП.
18. Исчисление показателей ВВП в постоянных ценах
19. Национальное богатство. Классификация его элементов. Оценка национального богатства страны.
20. Виды оценки и износ основных фондов.
21. Баланс основных фондов. Показатели состояния, движения и использование основных фондов.
22. Структура финансового рынка. Кредитный рынок (общие понятия, размер кредитных вложений, средняя процентная ставка, ее динамика).
23. Кредитный рынок (валовой доход за пользование кредитами, возвратность кредита, кредитоотдача).
24. Финансы предприятия.
25. Фондовый рынок.
26. Валютный рынок.
27. Статистическое изучение инвестиций.
28. Задачи статистики цен. Динамика средних цен.
29. Индексы цен Ласпейреса, Пааше, Фишера, Лоу. Использование индексов цен.
30. Показатели статистики уровня жизни населения.
Дата добавления: 2018-05-01; просмотров: 774; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
