Классификация численных методов решения задачи Коши для уравнения 1-го порядка

Вывод основного уравнения. Пусть уравнение (1) разрешено относительно 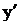. Имеем задачу

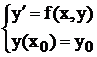. (5.2)

Все численные методы решения задачи (2) в качестве основного блока имеют некую процедуру вычисления значения у_i₊₁, если известно у_i и некоторые другие параметры. Т.е. вначале задаётся точка (х₀, у₀), по ней вычисляем точку (х₁, у₁), затем тем же способом вычисляем (х₂, у₂), и т.д. до конца таблицы.

Пусть у(х) – решение задачи (2). Подставим его в формулу (2) – получим тождество y`(x) º f(x, y(x)). Проинтегрируем его в пределах от х_i до x_i₊₁= х_i + h:

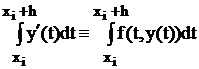. Отсюда имеем: 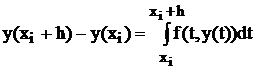. Или

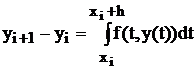. (5.3)

Формула (3) – интегральная форма задачи (2). Из этого уравнения надо найти у_i₊₁. Для построения численного метода необходимо воспользоваться какой-нибудь аппроксимацией интеграла (3) (квадратурной формулой). Получим основное уравнение

у_i₊₁– у_i »Ф(х_i , h, y_i_+1–_k,…, y_i , y_i₊₁), (5.4)

где Ф(…) – функция, являющаяся аппроксимацией интеграла в правой части формулы (3). Тип конкретного численного метода в основном определяется

а) выбранной аппроксимацией, т.е. видом функции Ф;

б) способом решения алгебраического уравнения (4).

Основные классы численных методов

1. Если в (4) k =1, то имеем уравнение у_i₊₁– у_i »Ф(х_i , h, y_i , y_i₊₁), т.е. не используются более ранние значения функции, чем y_i . В этом случае метод называется одношаговым. Если k > 1, т.е. надо задать y_i_–1, y_i_–2 и т.д., то метод будет многошаговым.

Одношаговые методы называются также самостартующими, т.к. для того, чтобы начать расчёты есть вся необходимая информация – начальная точка y₀ задана по условию задачи. При многошаговых методах для начала расчётов надо дополнительно определить несколько начальных точек из каких-то источников. Например, их вычисляют одношаговым методом, а дальше уже применяют многошаговый алгоритм. Очень часто такая сложность оправдана, т.к. многошаговые методы во многом лучше одношаговых.

2. Если Ф не зависит от y_i₊₁, то решить уравнение (4) очень просто:

у_i₊₁» у_i +Ф(х_i , h, y_i_+1–_k,…, y_i , y_i₊₁),

т.е. получим явную формулу для y_i₊₁. Соответствующие методы называются явными. В противоположность им, методы, в которых функция Ф зависит от у_i₊₁, называются неявными. При их реализации при каждом i возникает необходимость решения относительно у_i₊₁ некоторого нелинейного уравнения.

Три простейших метода. Получим формулы трёх простейших численных методов, используя простые (не составные) формулы численного интегрирования для аппроксимации интеграла (5.3).

1) Воспользуемся формулой левых прямоугольников (см. рисунок), известной из курса математического анализа:

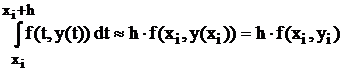= Ф(х_i , h, у_i).

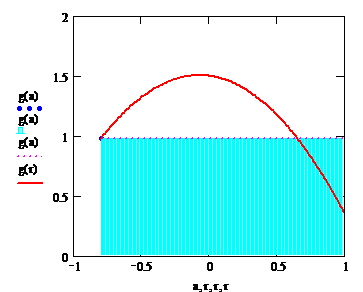
Функция Ф не зависит от у_i₊₁ и в ней k = 1. Следовательно, получаем явный одношаговый метод

у_i₊₁ = у_i + h f(х_i , у_i), (5.5)

называемый явным методом Эйлера.

Пример 5.3. Требуется решить задачу Коши

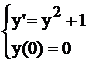Здесь f(x, y) = y² + 1. Аналитическое решение задачи y = tg x. Для этого уравнения формула (5) имеет вид

у_i₊₁ = у_i + h [(у_i)²+ 1].

2) Воспользуемся формулой трапеций (4.1), согласно которой интеграл (5.3) имеет следующий вид:

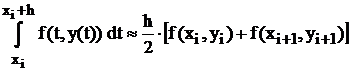При такой аппроксимации интеграла правая часть равенства (4) зависит от у_i₊₁ и поэтому имеем неявный одношаговый метод вида

у_i₊₁ – у_i = 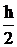[ f (x_i , у_i ) + f (x_i₊₁ , у_i₊₁ ) ], (5.6)

называемый неявным методом Эйлера. Согласно этому методу, в примере 5.3 для искомого значения у_i₊₁ будем иметь квадратное уравнение,

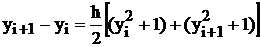решив которое, получим расчетную формулу:

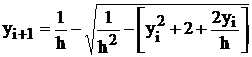В общем случае уравнение (6) может не иметь аналитического решения. Тогда для организации расчетов по методу (6) можно воспользоваться каким-нибудь численным алгоритмом решения уравнений для определения значения у_i₊₁ при каждом i (например, методом обратной интерполяции).

3) Другой способ реализации метода (6) без непосредственного решения уравнения относительно у_i₊₁ состоит в соединении явного и неявного методов. Вместо точного значения у_i₊₁ в правую часть равенства (6) подставляется его приближенное значение, найденное по формуле явного метода (5), а затем применяется формула (6). В результате получаем следующие расчетные формулы:

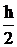= у_i + h f(х_i , у_i); у_i₊₁ = у_i + [ f(x_i, у_i ) + f(x_i₊₁ , ) ]. (5.7)

Такая идея соединения явного и неявного методов носит название схемы прогноза и коррекции. На первом шаге по явной формуле получается величина , называемая прогнозом, которая затем корректируется с использованием формулы неявного метода. Полученное значение у_i₊₁ считается окончательным искомым значением функции у(х) в i + 1-й точке. Метод (7) является одним из простейших вариантов такой схемы и называется модифицированным методом Эйлера или методом Эйлера-Коши.

Подставив левую формулу (7) в правую, получим единую расчетную формулу, которая для примера 5.3 будет иметь вид

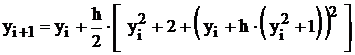Точность и устойчивость

Свойства задачи Коши

Прежде чем выбрать метод решения какой-либо вычислительной задачи, необходимо исследовать свойства этой задачи, т.к. в неустойчивых задачах наличие даже малых погрешностей вносит большое искажение в решение и даже самый лучший численный метод не может исправить положение. В задаче Коши исследованию подлежат два типа устойчивости: по начальному условию и по правой части.

Устойчивость по начальному условию. Пусть у₀ – некое начальное условие задачи (5.2), а 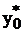= у₀ – e₀ – возмущённое начальное условие, т.е. заданное с погрешностью e₀. Определим, приведёт ли эта погрешность в начальных условиях к накоплению ошибки в решении.

Пусть

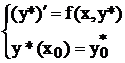– (5.8)

возмущённая задача Коши, т.е. с погрешностью в начальном условии. Вычтем из уравнения (5.2) уравнение (5.8):

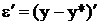= f(x, y) – f(x, y*).

Воспользуемся формулой конечных приращений Лагранжа, которая для произвольной функции g(x) и произвольных значений аргумента x = a и x = b имеет вид: 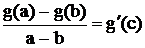, где сÎ(a, b) – некоторая точка, наклон касательной в которой равен наклону секущей, проходящей через точки a и b (см. рисунок).

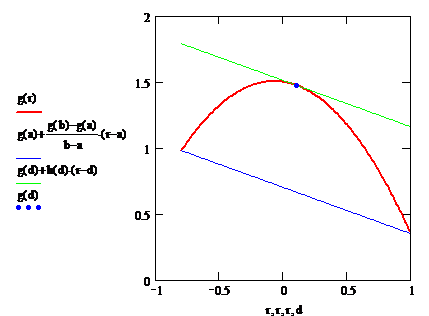
Применим формулу Лагранжа к функции f(x, y), полагая a = y(x), b = y*(x), c = 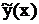Î(y(x), y*(x)):

f(x, y(x)) – f(x, y*(x)) = 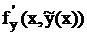×[y(x) – y*(x)].

Отсюда имеем дифференциальное уравнение относительно 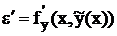e:

×e

с начальным условием e(x₀) = y₀ – 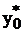= e₀. Полученное уравнение является линейным однородным, его решение имеет вид:

e(x) = e₀×exp 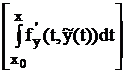= e₀×C(x).

Здесь C(x) – коэффициент роста ошибки с увеличением х. Если 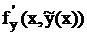> 0, то показатель экспоненты также положителен и С(х) возрастает. Вместе с ним растёт и погрешность решения. При 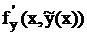< 0 получим, что С(х) убывает, а погрешность решения затухает. Если 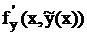меняет знак, то проанализировать рост ошибки сложно.

Пример 5.4. Пусть имеем задачу Коши

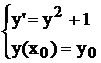f(x, y) = y² +1, следовательно 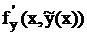= 2у. При у > 0 будет 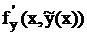> 0 и погрешность возрастает, а при у < 0 будет 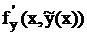< 0 и погрешность убывает. Проверим это. Точное решение этой задачи у = tg[(x – x₀) + arctg(y₀)]. Рассмотрим два случая.

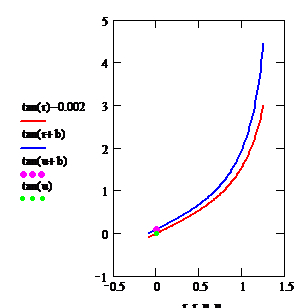
1. x₀ = 0, xÎ[0; 1.3]. Пусть у₀= 0, e₀ = –0.1, т.е. 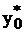= 0.1. Тогда y(x) = tg(x), y*(x) = tg(x+0.099669). y ³0. Графики обеих кривых – на рисунке. Видно, что линии расходятся, т.е. погрешность возрастает.

– точное решение – возмущённое решение

Дата добавления: 2018-04-15; просмотров: 719; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 23

Мы поможем в написании ваших работ!