Метод дробления шага. Правило Рунге

Стр 1 из 3Следующая ⇒

Тема 4. Численное ИНТЕГРИРОВАНИЕ В прикладных исследованиях часто возникает необходимость вычисления значения определенного интеграла , К сожалению, в подавляющем большинстве случаев получить значение интеграла с помощью формулы Ньютона-Лейбница или других аналитических методов не удается. Так, интеграл широко используется при исследовании процессов массо- и теплообмена, в статистической физике и теории вероятностей. Однако его значение не может быть выражено в виде конечной комбинации элементарных функций. При разработке численных методов нахождения значения определенных интегралов наиболее распространенным подходом является аппроксимация. Подынтегральную функцию f(x) на отрезке [a, b] приближают некоторой функцией F(x), которая легко интегрируется аналитически. Затем полагают . Если функция f(x) задана аналитически, то ставится вопрос об оценке погрешности такой замены.

Формула трапеций

1.1. Вывод формулы. Пусть функция f(x) интерполируется на [a, b] многочленом 1-й степени: F(x) = P₁(x) = y₀ + (х – x₀) ×D₁[x₀, x₁], где x₀= a, x₁= b. Обозначим h = x₁–x₀. Или Тогда

I*= .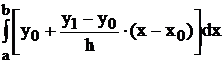

Сделаем замену переменных t = x – x₀, получим

I*= = =

После интегрирования и преобразования получим следующую формулу:

» [f(a) + f(b)] = 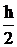[f(x₀) + f(x₁)] = I*, (4.1)

называемой формулой трапеций. Геометрически она означает замену площади криволинейной трапеции обычной трапецией (рис. 4.1), отсюда название формулы.

Рис. 4.1. Геометрическая интерпретация формулы трапеций

1.2. Погрешность формулы. Воспользуемся известной оценкой (3.9) погрешности интерполирования многочленом P₁(x):

R₁(z) = .

Имеем: R₁ = f(x) – F(x) Þ D = I – I* = = =

= = .

Здесь мы опять сделали замену переменных t = x – x₀. Тогда x = t + x₀, а x – x₁ = t + (x₀ – x₁) = t – (x₁ – x₀) = t – h. Отсюда

= = – f’’(x)× .

Итак,

D_ТРАП = – f’’(x)× , xÎ(a, b). (4.2)

Знак “–” означает, что при f’’ > 0 формула (4.1) дает значение интеграла с избытком, а при f’’ < 0 – с недостатком. На рис. 4.1 функция f(x) вогнута, т.е. f’’ < 0, следовательно, I* < I. При f’’ = 0, т.е. если f(x) = P₁(x), формула (4.1) не содержит погрешности и абсолютно точна.

Формула Симпсона

2.1. Вывод формулы. Пусть функция f(x) интерполируется на [a, b] многочленом 2-й степени:

F(x) = P₁(x) = y₀ + (х – x₀) ×( D₁[x₀, x₁] + (х – x₁) ×D₂[x₀, x₁, x₂] ),

где x₀ = a, x₁ = (a + b)/2, x₂= b, h = x_i+1 – x_i. Преобразуем формулу, используя явное выражение для D₁[x₀, x₁] = и D₂[x₀, x₁, x₂] = :

P₁(x) = y₀ + ×(х – x₀) + ×(х – x₀)×(х – x₁).

Сделаем замену переменных t = x – x₀. Тогда x = t + x₀, а x – x₁ = t – h. После интегрирования и преобразования получим следующую формулу:

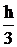» [ f (x₀) + 4f (x₁) + f (x₂) ] = I*, (4.3)

называемой формулой Симпсона. Ее геометрический смысл представлен на рис. 4.2.

Рис. 4.2. Геометрическая интерпретация формулы Симпсона

Оценка погрешности формулы Симпсона.

Метод вывода оценки погрешности, применённый для формулы трапеции, не годится для формулы Симпсона. Поэтому без доказательства примем следующую оценку погрешности формулы (4.3):

D_СИМП= I – I* = , xÎ[ x₀ , x₂]. (4.4)

Знак “–” означает, что при f ⁽⁴⁾ > 0 формула (4.3) дает значение интеграла с избытком, а при f ⁽⁴⁾ < 0 – с недостатком. На рис. 4.3 функция f(x) представляет собой многочлен 4-й степени с постоянным значением f ⁽⁴⁾ < 0. Из рисунка видно, что площадь фигуры под графиком f(x) (окрашенная область) больше, чем под F(x). Следовательно, I* < I. При f ⁽⁴⁾ = 0, т.е. если f(x) = P₃(x), формула (4.3) не содержит погрешности и абсолютно точна. Это видно на рис. 4.2 – f(x) представляет собой многочлен 3-й степени и площади под f(x) и под F(x) абсолютно одинаков, хотя сами функции не совпадают.

Рис. 4.3. При f ⁽⁴⁾ < 0 формула Симпсона дет результат с недостатком

3. Составные формулы численного интегрирования

Описанные формулы численного интегрирования легко обобщить на случай применения многочленов более высоких степеней и тем самым добиться улучшения точности решения задачи (подобный метод широко применяют, при этом, в частности, получаются так называемые квадратурные формулы Ньютона-Котеса). Однако, более перспективен другой способ, основанный на кусочной аппроксимации подынтегральной функции многочленами невысокой степени – 1-й или 2-й.

Идея метода: разбить отрезок [a, b] на n частей и на каждой части применить формулу трапеций или Симпсона. Из формул (4.2) и (4.4) видно, что при h < 1 погрешность этих формул уменьшается.

3.1. Составная формула трапеций. Разобьём отрезок [a, b] на n частей равноотстоящими точками x₀ = a, x₁ = a + h, …, x_n = b, и на каждой части [x_i, x_i₊₁] применим формулу трапеций:

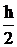» ×( y_i + y_i+1).

Получим

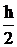» ×[( y₀ + y₁) + ( y₁ + y₂) + … + ( y_n–1 + y_n)] Þ

» h× – (4.5)

составная формула трапеций. Её геометрический смысл – подынтегральная функция заменяется ломанной.

3.2. Оценка погрешности. Очевидно, погрешность формулы (4.5) равна сумме погрешностей на каждом i-м интервале. Воспользуемся формулой (4.2), получим = – , где x_iÎ[x_i, x_i₊₁].

Обозначим m = – среднее арифметическое значений второй производной, а также m = , M = . По известному свойству среднего арифметического имеем: m £ m£ M.

Из математического анализа известна 2-я теорема Больцано-Коши: если функция y(x) непрерывна на отрезке, то она принимает все свои значения, от минимального до максимального. Иными словами, для любого р, такого что min y(x) £ p £ max y(x), уравнение p = y(x) всегда имеет решение при непрерывной функции у(х). Для разрывной функции это, вообще говоря, неверно (см. рис. 4.4).

Рис. 4.4. Иллюстрация ко 2-й теореме Больцано-Коши: непрерывная и разрывная функции.

Если f’’(x) непрерывна на [a, b], то к ней применима указанная теорема при р = m. Значит, существует такая точка xÎ[a, b], что m = f’’(x). Следовательно,

= n×m = n×f ’’(x). Тогда

= – = – .

Следовательно,

= – . (4.6)

3.3. Составная формула Симпсона. Разобьём отрезок [a, b] на n частей, где n – чётно. Применим формулу Симпсона к каждому двойному отрезку [x₂_i_–2, x₂_i]. Тогда

» ×[(y₀ + 4y₁+ y₂) + (y₂ + 4y₃+ y₄) + … + (y_n–2 + 4y_n–1+ y_n)].

Заметим, что y₂, y₄,… y_n_–2 повторяются дважды. Отсюда

» ×[( y₀ + y_n) + 4S_нечётн + 2S_чётн] (4.7)

составная формула Симпсона.

Здесь S_нечётн = y₁+ y₃+ … + y_n_–1, S_чётн= y₂+ y₄+ … + y_n_–2.

3.4. Оценка погрешности. Для оценки погрешности формулы (4.7) воспользуемся оценкой (4.4) погрешности простой формулы. Применим тот же метод, что и для составной формулы трапеции. Получим

= – . (4.8)

Задание. Вывести формулу (4.8) самостоятельно.

Метод дробления шага. Правило Рунге

Формулы (4.6) и (4.8) для практики неудобны, т.к. значения f⁽^k⁾ (x) обычно неизвестны. Правило Рунге позволяет найти достаточно точные оценки погрешности, используя значения I*, вычисленные при различных h.

Согласно полученным оценкам, погрешность составных формул численного интегрирования имеет вид

I – I^h » C×h^m, (4.9)

где I и I^h – точное значение интеграла и значение, найденное по составной формуле при шаге h, соответственно; С – некоторая константа; m – порядок точности численного метода (согласно формулам (4.6) и (4.8), m = 2 для формулы трапеции и m = 4 для формулы Симпсона).

Уменьшим шаг вдвое. Будем иметь:

I – I^h/2 » 2^–m×C×h^m. (4.10)

Вычтем (4.10) из (4.9). Получим: I^h^/2 – I^h » 2^–^m×C×h^m(2^m – 1) = (I – I^h^/2)(2^m – 1).

Следовательно,

. (4.11)

Формула (4.11) – оценка погрешности вычисления I^h^/2 по правилу Рунге. Если значение правой части приближенного равенства (4.11) окажется меньше предельно допустимой погрешности e, то можно считать I^h^/2 ответом задачи. В противном случае – требуемая точность не достигнута и необходимо использовать более мелкий шаг, т.е. продолжить процесс дробления шага.

Замечание. При приближённом вычислении интегралов, абсолютная величина | I | которых мала, использование значения абсолютной погрешности D для контроля точности необоснованно, более приемлема относительная погрешность d. Поэтому при использовании правила Рунге рекомендуется следующий критерий останова процесса дробления шага:

если | I^h^/2 | ³ 1, то заканчивать при ,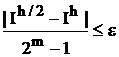

если | I^h^/2 | < 1, то заканчивать при .

Пример использования правила Рунге см. «Вычислительная практика» Пример 4.4. Там же в разделе 5 приведены тестовые примеры для программ численного интегрирования.

Задание. Обобщите правило Рунге на случай, когда шаг h на каждой итерации уменьшается не в 2, а в s раз.

Дата добавления: 2018-04-15; просмотров: 1919; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!