Описание лабораторной установки и хода выполнения лабораторной работы
Лабораторная работа 1.3
Определение момента инерции твердого тела
Основные понятия, определения, законы и формулы динамики вращательного движения твердого тела
1.Момент силы относительно точки O−величина, равная векторному произведению радиуса-вектора, проведенного из точки O в точку приложения силы, на вектор силы:
.
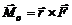2.Момент силы относительно оси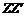 
−это составляющая (или проекция) вдоль этой оси момента силы относительно любой точки оси:
.
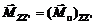3.Момент инерции материальной точки относительно оси 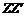− это величина, равная произведению массы материальной точки на квадрат расстояния от точки до оси:
.
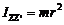4.Момент инерции тела относительно оси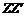 − это величина, равная сумме моментов инерции материальных точек, составляющих тело, относительно этой оси:
.
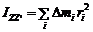5.Формула момента инерции однородного цилиндра (диска) массой m и радиусом R относительно оси, совпадающей с геометрической осью цилиндра:
.
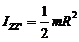Формула момента инерции тонкого однородного стержня массой m и длиной lотносительно оси, перпендикулярной оси стержня и проходящей через середину стержня:
.
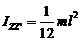Формула момента инерции однородного шара массой m, радиусом R относительно оси, проходящей через центр шара:
.
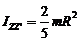6.Теорема Штейнера.Момент инерции тела относительно некоторой оси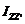 
равен моменту инерции этого тела относительно оси, 
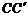параллельной оси 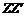и проходящей через центр масс тела, плюс произведение массы тела m на квадрат расстояния a между указанными осями:
|
|
|
.
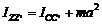7. Основной закон динамики вращательного движения твердого тела. Угловое ускорение, с которым вращается твердое тело вокруг неподвижной оси, равно отношению векторной суммы моментов сил, действующих на тело, относительно оси вращения к моменту инерции этого тела относительно этой оси:
.
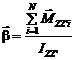8. Момент импульса материальной точки относительно точки O− это векторная величина, равная векторному произведению радиуса-вектора, проведенного из точки O в материальную точку, на вектор импульса материальной точки:
.
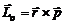9. Момент импульса материальной точки относительно оси 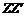− это составляющая (проекция) вдоль этой оси момента импульса материальной точки относительно любой точки O, лежащей на оси:
.
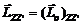10. Момент импульса системы материальных точек относительно оси 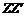−величина, равная векторной сумме моментов импульса всех N материальных точек, составляющих систему, относительно этой оси:
.
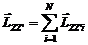11. Формула момента импульса твердого тела, вращающегося вокруг неподвижной оси:
.
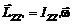12. Закон сохранения момента импульса. Момент импульса замкнутой системы материальных точек остается постоянным:
|
|
|
.
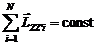13.Формула кинетической энергии тела, вращающегося вокруг неподвижной оси:
.
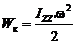Описание лабораторной установки и хода выполнения лабораторной работы
Момент инерции твердого тела можно определить аналитически, применяя для расчета известные формулы, и экспериментально, изучая вращение тела вокруг неподвижной оси. Рассмотрим один из способов экспериментального определения момента инерции твердого тела относительно закрепленной оси.
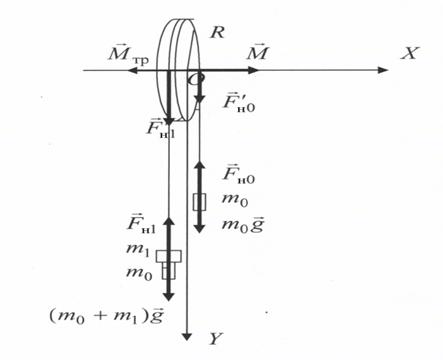
Определим момент инерции блока, представляющего собой однородный диск, относительно горизонтальной оси, проходящей через центр масс блока, наблюдая его вращение вокруг этой оси (рисунок 3.1). Если к концам нити, перекинутой через блок, подвесить грузы одинаковой массой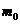 
, то система блок–нить–грузы будет неподвижной.
|
| Рисунок 3.1 |
На один из грузов массой m0 положим перегрузок массой m1, чтобы грузы пришли в движение. Применяя второй закон Ньютона к каждому из грузов, подвешенных к концам нити, можно записать следующие уравнения движения:
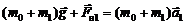, (3.1)
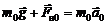. (3.2)
Согласно основному закону динамики вращательного движения уравнение движения блока имеет следующий вид:
|
|
|
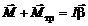, (3.3)
где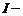 
момент инерции блока относительно оси вращения; 
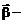его угловое ускорении; 
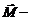момент силы трения покоя между нитью и блоком, которая вращает блок; действие этой силы приводит к тому, что силы натяжения нити справа и слева от блока имеют разную величину; 
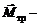момент силы трения на оси закрепления блока.
Момент инерции блока и моменты сил берутся относительно оси вращения.
Запишем уравнения (3.1), (3.2) и (3.3) в проекциях на оси OY и OX соответственно:
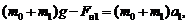(3.1')
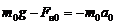, (3.2')
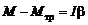. (3.3')
Действие силы трения покоя между нитью и блоком приводит к тому, что силы натяжения нити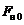 
и 
(и 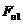соответственно 
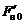и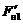 
) не равны друг другу. Их разность и составляет величину силы трения между нитью и блоком. Поэтому момент последней силы относительно оси вращения (также как относительно центра блока O) равен:
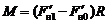, (3.4)
где R − радиус блока.
Так как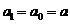 
, 
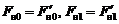, то вместо системы уравнений (3.1')−(3.3'), (3.4) получим систему:
|
|
|
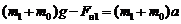, (3.5)
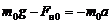, (3.6)
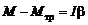, (3.7)
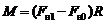. (3.8)
Из равенств (3.5) и (3.6) можно найти:
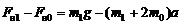. (3.9)
Ускорение a поступательного движения груза является тангенциальным ускорением точек обода блока и поэтому связано с угловым ускорением блока известным соотношением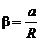 
.
С другой стороны, из формулы пути при равноускоренном движении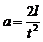 
, где l – расстояние, которое прошел каждый груз за время 
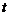из состояния покоя. Учитывая это, получим:
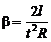. (3.10)
С учетом соотношений (3.9) и (3.10) равенство (3.8) запишется следующим образом:
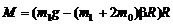. (3.11)
Если использовать перегрузки сначала массой m1, а потом массой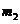 
, то (при 
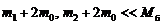, где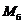 
− масса блока) момент сил трения на оси блока 
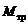можно считать постоянным. Но различие масс перегрузков приведет к различным значениям моментов сил трения покоя между нитью и блоком и, следовательно, к различным угловым ускорениям 
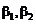в указанных двух случаях. Поэтому на основании формулы (3.11) в случае перегрузка массой 
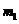будем иметь момент силы трения покоя между нитью и блоком
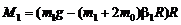, (3.12)
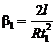, (3.13)
а в случае перегрузка массой m2:
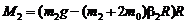, (3.14)
. (3.15)
При этом согласно уравнению (3.3') указанные моменты сил удовлетворяют равенствам:
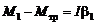, (3.16)
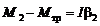. (3.17)
Из уравнений (3.16) и (3.17) можно определить момент инерции блока:
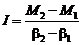(3.18)
и момент сил трения на оси блока:
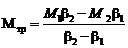. (3.19)
Величины I и Mтр можно определить графически, построив график функции β = β(M). Он в соответствии с формулой (3.3) имеет вид прямой линии (рисунок 3.2), уравнение которой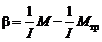 
.
Дата добавления: 2018-05-01; просмотров: 205; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!