Непосредственное вычисление вероятности (классическая вероятность)
1. В коробке 5 синих, 4 красных и 3 зеленых карандаша. Наудачу вынимают 3 карандаша. Какова вероятность того, что: а) все они одного цвета; б) все они разных цветов; г) среди них 2 синих и 1 зеленый карандаш?
● а) Р(А1) =  =
= 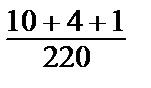 =
=  ≈ 0,07;
≈ 0,07;
б) Р(А2) =  =
=  =
=  =
=  ≈ 0,27;
≈ 0,27;
в) Р(А3) =  =
=  =
=  ≈ 0,14.
≈ 0,14.
2. Дано 6 карточек с буквами Н, М, И, Я, Л, О. Найти вероятность того, что:
а) получится слово ЛОМ, если наугад одна за другой выбираются три карточки;
б) получится слово МОЛНИЯ, если наугад одна за другой выбираются шесть карточек и располагаются в порядке возрастания.
● Все буквы разные (  – число размещений из n разных элементов по m:
– число размещений из n разных элементов по m:  =
= 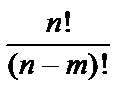 ,Pn – число перестановок из n разных элементов: Pn = n!).
,Pn – число перестановок из n разных элементов: Pn = n!).
а) Р(А1) =  =
= 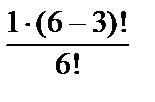 =
=  ≈ 0,008.
≈ 0,008.
Можно «в лоб»: вероятность вытащить 1-й букву Л Р(Л) =  , 2-й – букву О Р(О/Л) =
, 2-й – букву О Р(О/Л) =  , 3-й – букву М
, 3-й – букву М
Р(М/ЛО) = 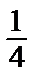 . Т.о., Р(ЛОМ) = Р(Л) · Р(О/Л) · Р(М/ЛО) =
. Т.о., Р(ЛОМ) = Р(Л) · Р(О/Л) · Р(М/ЛО) =  ·
·  ·
·  =
=  ≈ 0,008.
≈ 0,008.
б) Р(А2) =  =
= 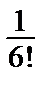 =
=  ≈ 0,0014.
≈ 0,0014.
Можно «в лоб»: вероятность вытащить 1-й букву М Р(М) =  , 2-й – букву О Р(О/М) =
, 2-й – букву О Р(О/М) =  , 3-й – букву Л
, 3-й – букву Л
Р(Л/МО) =  , 4-й – букву Н Р(Н/МОЛ) =
, 4-й – букву Н Р(Н/МОЛ) =  , 5-й – букву И Р(И/МОЛН) =
, 5-й – букву И Р(И/МОЛН) = 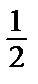 , 6-й – букву Я
, 6-й – букву Я
Р(Я/МОЛНИ) =  = 1. Т.о., Р(МОЛНИЯ) = Р(М) · Р(О/М) · Р(Л/МО) · Р(Н/МОЛ) · Р(И/МОЛН) · Р(Я/МОЛНИ) =
= 1. Т.о., Р(МОЛНИЯ) = Р(М) · Р(О/М) · Р(Л/МО) · Р(Н/МОЛ) · Р(И/МОЛН) · Р(Я/МОЛНИ) =  ·
· 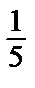 ·
·  ·
·  ·
·  · 1 =
· 1 =  ≈ 0,0014.
≈ 0,0014.
3. Код домофона состоит из 8 цифр, которые могут повторяться. Какова вероятность того, что случайно набирая цифры, можно угадать нужный код?
● Подсчитаем общее количество возможных комбинаций: 1-й можно набрать любую из 10 цифр (10 вариантов), аналогично, любую из 10 цифр можно набрать в каждом из оставшихся 7 наборов. Т.о., общее количество возможных комбинаций n = 108.
|
|
|
Открывает дверь единственная комбинация: m = 1.
Т.о., Р(А) =  =
=  .
.
4. Восемь друзей распределяют места за круглым столом по жребию. Какова вероятность того, что два из них, а именно А и В, будут сидеть рядом?
● СобытиеС = «друзья сидят рядом». Р(С) =  . n – общее число рассадок, m– число рассадок, когда А и В сидят рядом.
. n – общее число рассадок, m– число рассадок, когда А и В сидят рядом.
Так как за круглым столом выбор первого человека не влияет на чередование элементов, то первым можно
взять любого, а оставшихся упорядочим относительно выбранного. Это действие можно осуществить (N – 1)! способами, где N – число друзей.
Т.о., n = 7!.
«Склеим» А и В. Получим «одного человека» АВ или ВА (2 варианта). Всего получим 7 «друзей», которых можно рассадить 6! способами. Т.о., m = 2 ·6!.
Р(С) =  =
=  =
= 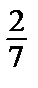 .
.
Другое решение: А может сесть на любое место. В выбирает из оставшихся n = 7 мест m = 2 места (слева или справа от А). Значит, Р(С) =  =
= 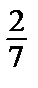 .
.
5. На 5 карточках написано по одной цифре из набора 1, 2, 3, 4, 5. Наугад выбирают 2 карточки. Какова вероятность того, что число на второй карточке больше, чем на первой?
● Задача решается по формуле классической вероятности Р(А) =  , где n-общее число вариантов, m- число благоприятных вариантов. Найдем число всех вариантов. Если на первой карточке 1 то второй могут быть цифры 2, 3, 4, 5, итого 4 варианта. Если на первой карточке цифра 2, то на второй карточке могут быть цифры 1, 3, 4, 5, итого 4 варианта. Аналогично если на первой карточке цифра 3 то опять буде 4 варианта, если на первой карточке цифра 4, тоже 4 варианта и если цифра 5 то все равно 4 варианта. Получается что с каждой цифрой по 4 варианта, всего 20 вариантов. Т.о., n= 4 · 5 = 20.
, где n-общее число вариантов, m- число благоприятных вариантов. Найдем число всех вариантов. Если на первой карточке 1 то второй могут быть цифры 2, 3, 4, 5, итого 4 варианта. Если на первой карточке цифра 2, то на второй карточке могут быть цифры 1, 3, 4, 5, итого 4 варианта. Аналогично если на первой карточке цифра 3 то опять буде 4 варианта, если на первой карточке цифра 4, тоже 4 варианта и если цифра 5 то все равно 4 варианта. Получается что с каждой цифрой по 4 варианта, всего 20 вариантов. Т.о., n= 4 · 5 = 20.
Найдем количество благоприятных вариантов. Если на первой карточке цифра 1 то на второй могут быть цифры 2, 3, 4, 5, все они больше 1. Получается 4 варианта. Если на первой карточке цифра 2 то на второй могут быть цифры 1, 3, 4, 5. Из них только три цифры больше 2. Значит, 3 варианта. Если на первой карточке цифра 3, то будет только 2 варианта (если на второй карточке цифры 4 или 5). Если на первой карточке цифра 4, то только 1 вариант (цифра 5 на второй карточке) . Если на первой карточке цифра 5 то вариантов нет (все цифры меньше 5). Итак благоприятных вариантов всего получается m=4+3+2+1=10.
Окончательно, Р(А) =  = 0,5.
= 0,5.
|
|
|
6. Из колоды в 36 карт извлекаются наудачу 4 карты. Какова вероятность событий: А = «все извлеченные карты пиковой масти», В = «среди этих 4-х карт окажется хотя бы один король»?
|
|
|
● а) Общее число событий n =  =
=  = 58905.
= 58905.
Благоприятное число событий m =  =
=  = 126.
= 126.
Тогда искомая вероятность будет равна Р(А) =  =
=  ≈ 0,0021.
≈ 0,0021.
Или так.
1-я пика: р1 = 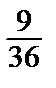 ; 2-я пика: р2 =
; 2-я пика: р2 =  ; 3-я пика: р3 =
; 3-я пика: р3 =  ; 4-я пика: р4 =
; 4-я пика: р4 =  .
.
Р(А) = р1 · р2 · р3 · р4 =  ≈ 0,0021.
≈ 0,0021.
б) Общее число событий n =  =
=  = 58905.
= 58905.
Благоприятное число событий для противоположного события  = «среди извлеченных карт нет ни одного короля» t =
= «среди извлеченных карт нет ни одного короля» t =  =
=  = 35960.
= 35960.
Тогда искомая вероятность будет равна Р(В) = 1 – Р(  ) = 1 –
) = 1 –  = 1 –
= 1 –  ≈ 0,39.
≈ 0,39.
7. 12 человек, среди которых Петров и Иванов, размещаются в гостинице, в которой есть один 4-местный, два 3-местных и один 2-местный номер. Какова вероятность события А , состоящего в том, что Петров и Иванов попадут в 2-местный номер?
● Число всех возможных размещений 12 человек в одном 4-местном, двух 3-местных и одном 2-местном номере равно числу перестановок из 12 элементов, среди которых 1 одного вида, 2 другого и 1 третьего, т. е.
n = 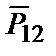 (4;3;3;2) =
(4;3;3;2) =  = 277200.
= 277200.
После того как Иванов и Петров будут размещены в 2-местном номере, остальные 10 человек должны быть размещены в одном 4-местном и двух 3-местных, это можно будет сделать следующим образом:
m =  (4;3;3) =
(4;3;3) =  = 4200.
= 4200.
Искомая вероятность P(A) =  =
=  =
=  ≈ 0,015.
≈ 0,015.
|
|
|
8. На отрезок АВ длины α наудачу нанесена точка С. Найти вероятность того, что меньший из отрезков АС и СВ имеет длину, большую, чем  .
.
●

Геометрическая вероятность. Задача эквивалентна следующей: какова вероятность попадания точкиС в интервал (E, F). Т.к. |EF| = α – 2·  =
= 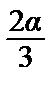 , то P(A) =
, то P(A) = 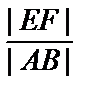 =
=  =
=  .
.
9. Минное заграждение состоит из мин, расположенных в одну линию на расстоянии 50 м одна от другой. Ширина корабля 20 м. Какова вероятность того, что корабль благополучно пройдет через заграждение?
●

Геометрическая вероятность. Если корабль подходит к заграждению под углом α, то он пройдет его по ширинеH = 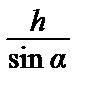 (см. рис.1). Это его т.н. эффективная ширина. Тогда вероятность того, что корабль благополучно пройдет через заграждение (см. рис.2) P(A) =
(см. рис.1). Это его т.н. эффективная ширина. Тогда вероятность того, что корабль благополучно пройдет через заграждение (см. рис.2) P(A) =  =
=  =
=  . Если корабль идет перпендикулярно заграждению, то α = 90°, и P(A) =
. Если корабль идет перпендикулярно заграждению, то α = 90°, и P(A) =  =
=  = 0,6.
= 0,6.
10. В шар вписан куб. Найти вероятность того, что выбранная наудачу внутри шара точка окажется внутри куба.
● Введем обозначения: событиеА- «попадание точки в куб»; R- радиус шара, a- ребро куба, V- объем шара, V1- объем вписанного куба.
Как известно, объем шара равен V =  πR3. Т.к. V1 = a3, а ребро куба выражается через радиус шара как a =
πR3. Т.к. V1 = a3, а ребро куба выражается через радиус шара как a =  , то V1 =
, то V1 =  R3 . Следовательно, P(A) =
R3 . Следовательно, P(A) =  =
=  =
=  ≈ 0,368.
≈ 0,368.
11. На отрезке единичной длины случайным образом появляется точка. Найти вероятность того, что расстояние от точки до концов отрезка больше 1/8.
● Вероятность искомого события равна P(A) =  , где L– длина всего отрезка, на котором может появиться точка (L= 1), l– длина отрезка, попадание точки на который, удовлетворяет условию задачи: l= 1 – 2 ·
, где L– длина всего отрезка, на котором может появиться точка (L= 1), l– длина отрезка, попадание точки на который, удовлетворяет условию задачи: l= 1 – 2 ·  =
=  (см. рис.). Т.о., P(A) =
(см. рис.). Т.о., P(A) =  =
=  = 0,75.
= 0,75.
12. Точка (c, q) наудачу выбирается из квадрата с вершинами (-1,-1), (1,-1), (1,1), (-1,1).
Найти вероятность того, что корни уравнения x2 + cx + q = 0, будут действительные.
● Вероятность искомого события равна P(A) =  , где S– площадь квадрата, из
, где S– площадь квадрата, из
которого выбирается точка (c, q). S = 2 · 2 = 4. s–площадь части данного квадрата, выбор точки из которого, удовлетворяет условию задачи . Корни уравнения действительные, если дискриминант D = c2 – 4q≥ 0 =>
ð
| 1 |
| -1 |
| -1 |
| 1 |
| -1, 1 |
| 1, 1 |
| -1, -1 |
| 1, -1 |
| 0 |
| q |
| c |
 c2. Следовательно (заштрихована на рис.),
c2. Следовательно (заштрихована на рис.),
s= 2 · (1 +  ) = 2 · (1 +
) = 2 · (1 +  ) = 2 · (1 +
) = 2 · (1 +  ) =
) =  .
.
Т.о., P(A) =  =
=  =
=  = 0,54.
= 0,54.
13. Сколько раз нужно бросить игральную кость, чтобы с вероятностью не меньше 0,6 хотя бы один раз выпало 6 очков?
● Имеем: р =  ; q = 1 – p =
; q = 1 – p =  ; требуемая вероятность Р = 0,6.
; требуемая вероятность Р = 0,6.
Вероятность заданного события в зависимости от числа бросаний 1 – qn.
Отсюда 1 – qn ≥ P =>qn ≤ 1 – P =>lnqn ≤ ln(1 – P) =>n ≥ 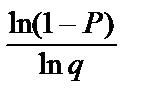 .
.
Подставим исходные данные и посчитаем: n ≥  =
=  ≈
≈  ≈ 5,1.
≈ 5,1.
Ответ: n = 6.
14. Из последовательности чисел 1, 2, 3, 4, … , 600 наудачу выбираются два числа. Какова вероятность того, что одно из них меньше 126, а другое больше 126?
● Выбрать число, меньшее 126, можно 125 способами, а большее 126 – 600 –126 = 474 способами.Значит, всего возможны m = 125·474 = 59250 способов выбрать два числа с указанными свойствами.
Выбрать два числа из 600 можно n =  =
=  =
=  = 179700 способами.
= 179700 способами.
По формуле классической вероятности P(A) =  =
=  ≈ 0,33.
≈ 0,33.
15. Натуральные числа от 1 до n расставлены случайно. Найти вероятность того, что числа 5, 6, 7 расположены рядом и притом в порядке возрастания.
● Общее число равновозможных исходов опыта, состоящего в расстановке n чисел по n местам равно
N = Pn = n!
СобытиеА = «числа 5, 6, 7 расположены рядом в порядке возрастания».
Три подряд идущие позиции можно выбрать n – 2 способами (позиции 1 – 3, 2 – 4, … , (n – 2) – n) . Оставшиеся n – 3 позиции занимаются произвольным образом другими числами 1, 2, 3, 4, 8, 9, …, n . Следовательно, число исходов, благоприятствующих событиюА, равно m = (n – 2) · (n – 3)! = (n – 2)!
По формуле классической вероятности P(A) =  =
=  =
=  .
.
16. Какова вероятность того, что произвольно взятое трехзначное число делится на 3?
● Всего трехзначных чисел n = 900 (1000 – 100) .
На 3 делятся числа, сумма цифр которых делится на 3. Из трехзначных это 102, 105, 108, … , 999. Эти числа образуют арифметическую прогрессию с а1 = 102, d = 3, am = 999. Для нахождения mвоспользуемся формулой am = а1 + (m– 1)·d . Отсюда:
999 = 102 + (m– 1)·3 =>(m– 1)·3 = 897 =>m– 1 = 299 =>m= 300.
По формуле классической вероятности P(A) =  =
=  =
= 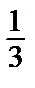 .
.
17. В группе 10 юношей и 10 девушек. Для дежурства на дискотеке путем жеребьевки выделяют 5 человек. Какова вероятность того, что в число дежурных войдут:
а) 5 юношей; б) 2 юноши и 3 девушки?
● Р(А) = 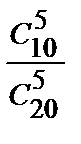 =
= 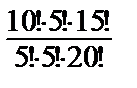 ≈ 0,016; Р(В) =
≈ 0,016; Р(В) =  ≈ 0,232.
≈ 0,232.
18. В урне 3 белых, 6 черных и 5 синих шаров. Из нее вынимают наудачу 2 шара. Какова вероятность того, что они окажутся разного цвета?
● Всего 14 шаров.
Вероятность вытащить синий и черный шары Р(С,Ч) =  =
=  .
.
Вероятность вытащить белый и синий шары Р(Б,С) =  =
= 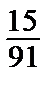 .
.
Вероятность вытащить белый и черный шары Р(Б,Ч) =  =
=  .
.
По теореме о сложении вероятностей: Р(А) = Р(С,Ч) + Р(Б,С) + Р(Б,Ч) =  +
+ 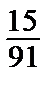 +
+  =
=  ≈ 0,7.
≈ 0,7.
19. Из колоды в 36 карт вынимают наудачу 4 карты. Найти вероятности событий: А = «все карты дамы»,
В = «две карты из четырех - шестерки». Решить задачу для схемы выбора:
а) без возвращения; б) с возвращением.
● а) без возвращения: Р(А) =  =
=  =
=  ≈ 0,000017;
≈ 0,000017;
Р(В) = 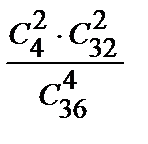 ≈ 0,051;
≈ 0,051;
б) с возвращением: Р(А) =  =
=  ≈ 0,00015;
≈ 0,00015;
Р(В) = 

 ≈ 0,06 – схема Бернулли.
≈ 0,06 – схема Бернулли.
20. На плоскости нарисованы две концентрические окружности, радиусы которых 3см и 5см. Какова вероятность того, что точка, брошенная наудачу в большой круг, попадет в кольцо, образованное этими окружностями?
●

P(A) =  =
=  = 1 –
= 1 –  = 1 –
= 1 –  = 0,64.
= 0,64.
21. Стержень длины L ломают на три части. Найти вероятность того, что из этих частей можно построить треугольник.
● Без ограничения общности можно считать, что L= 1.









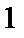












СобытиеА = «треугольник можно построить» произойдет, если будут выполнены условия: длина каждой из сторон меньше суммы длин двух других сторон, т.е. должны выполняться неравенства x + y > z, x + z > y, y + z > x. Эти неравенства с учетом системы неравенств 0 ≤ х ≤ 1, 0 ≤ у ≤ 1, 0 ≤ z ≤ 1, заданной условиями задачи, в декартовой прямоугольной системе координат Oxyz из куба OABCDEFG с единичными ребрами «вырезают» соответственно три пирамиды ODEG, OAEB, OCBG (каждое из неравенств определяет соответствующее полупространство). Оставшаяся фигура OBEFG содержит точки (x, y, z), удовлетворяющие всем записанным выше неравенствам, т.е. из отрезков длиной x, y, z можно построить треугольник.
Объем фигуры OBEFG легко подсчитать, если из объема куба OABCDEFG (равного 1) вычесть объемы трех пирамид ODEG, OAEB, OCBG, объем каждой из которых равен  Т.о., объем фигуры OBEFG равен VOBEFG = 1 – 3 ∙
Т.о., объем фигуры OBEFG равен VOBEFG = 1 – 3 ∙ 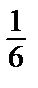 =
=  и P (A) =
и P (A) =  =
=  .
.
22. На паркет, составленный из правильных треугольников со стороной а, случайно падает монета радиуса r. Найти вероятность того, что монета целиком окажется внутри одного из треугольников.
●

По сути дела, мы бросаем монетку в один единственный треугольник. Это упрощает задачу.
Значение rдолжно быть достаточно мало по сравнению с a (насколько, можно подсчитать). В противном случае вероятность будет равна нулю.
Монета не будет пересекать треугольник АВС, если ее центр находится внутри треугольника А1В1С1, отстоящего от ΔАВС на расстоянии радиуса монеты r (см. рис.) (центр монеты должен попадать в ΔА1В1С1).
P(A) =  .
.
Т.к. треугольники АВС и А1В1С1 подобны, то их площади относятся, как квадраты линейных размеров. В качестве линейной величины возьмем радиус вписанной окружности.
Имеем: радиус вписанной в ΔАВС окружности Rб =  . Из рисунка: радиус вписанной в ΔА1В1С1окружности
. Из рисунка: радиус вписанной в ΔА1В1С1окружности
Rм = Rб– r=  – r .Т.о., P(A) =
– r .Т.о., P(A) =  =
=  =
= 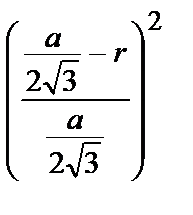 =
=  .
.
Дата добавления: 2018-04-15; просмотров: 10254; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
