Задачи для самостоятельного решения

ТЕОРИЯ ВЕРОЯТНОСТЕЙ (Практика 2)

Теория вероятностей (практика для САП, СМТ)

1. Комбинаторика

1. Сколькими способами можно разместить в 2-х комнатах 9 различных предметов?

●

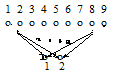
1-й предмет можно разместить в одной из 2-х комнат. 2-й – тоже, 3-й – тоже и т.д. Т.о., всего вариантов размещения в данной задаче 2·2·2·2·2·2·2·2·2 = 2⁹ = 512.

2. Сколькими способами можно распределить 6 разных книг между 3-мя школьниками?

●

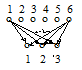
1-я книга может быть дать одному из 3-х школьников. 2-я – тоже, 3-я – тоже и т.д. Т.о., всего вариантов распределения 6 разных книг между 3-мя школьниками в данной задаче 3·3·3·3·3·3 = 3⁶ = 729.

3. Сколько различных букетов по 5 цветков в каждом можно составить, если в наличии есть достаточно много цветков 4-х видов?

● Это – задача на сочетания с повторениями. Различные неупорядоченные совокупности, состоящие из n элементов, каждый из которых принадлежат одному из m типов, называются сочетаниями из m(различных) элементов по n элементов с повторениями.

Например, из трех различных элементов a₁, a₂, a₃ можно составить такие сочетания с повторениями:

(a₁, a₁), (a₁, a₂), (a₁, a₃), (a₂, a₂), (a₂, a₃), (a₃, a₃).

Число различных сочетаний с повторениями из mпо n обозначается 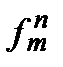иравно

= = .

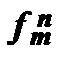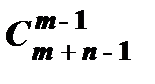Возьмем какое-нибудь сочетание из m по n. Запишем подряд столько единиц, сколько элементов 1-го типа в этом сочетании, затем поставим нуль; потом запишем столько единиц, сколько элементов 2-го типа, запишем нуль и т.д. Т.о. получим последовательность из nединиц и m – 1нулей (если элементов какого-либо типа нет, то единицы не пишем; нуль – граница между типами). Распределить nединиц на n+ m – 1 мест можно 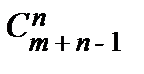способами (или распределить m – 1 нулей на n+ m – 1 мест можно 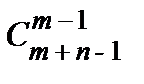способами).

В нашем случае N= = = 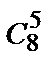= = 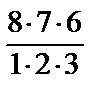56.

4. Сколько можно составить четырехзначных чисел таких, чтобы любые две соседние цифры были различными?

● На 1-м месте может стоять любая из 9 цифр (все, кроме 0). На 2-м месте не может стоять цифра, стоящая 1-й. Значит, на 2-м месте также могут стоять оставшиеся 9 цифр. Точно также, на 3-м и 4-м местах могут стоять 9 цифр (исключая предыдущую). Т.о., искомых чисел можно составить N= 9·9·9·9 = 9⁴.

5. Сколько различных «слов», состоящих из трех букв, можно образовать из букв слова

а) ЛЕТО, б) ШАЛУН?

● Эту задачу можно понимать по-разному.

а) Все буквы слов состоят из 4-х различных букв (которые не повторяются). Тогда: N= 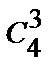= = 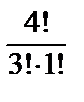4.

Все буквы составляемых слов состоят из 4-х букв Л, Е, Т, О, которые могут повторяются. Тогда: N= 4·4·4 = 4³

(на 1-м месте – одна из 4-х букв, на 2-м, 3-м– тоже).

б) Все буквы слов состоят из 5-х различных букв (которые не повторяются). Тогда: N= 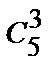= = 10.

Все буквы составляемых слов состоят из 5-х букв Ш, А, Л, У, Н, которые могут повторяются. Тогда: N= 5·5·5 = 5³

(на 1-м месте – одна из 5-х букв, на 2-м, 3-м – тоже).

6. Каждого из 6 студентов можно направить для прохождения практики на одно из 3-х предприятий. Сколькими различными способами это можно осуществить?

●

1-й студент может быть может быть отправлен на любое из 3-х предприятий. 2-й – тоже, 3-й – тоже и т.д. Т.о., всего вариантов распределения 6 студентов между 3-мя предприятиями 3·3·3·3·3·3 = 3⁶ = 729.

7. Сколько трехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, если

а) цифры не могут повторяться;

б) цифры могут повторяться;

в) числа должны быть четными (цифры могут повторяться);

г) числа должны делиться на 5 (цифры не могут повторяться)?

● а) Есть пять цифр - 0, 1, 2, 3, 4. В качестве сотен можно использовать только 4 цифры (без нуля, в противном случае число не будет трехзначным) , в качестве десятков - тоже 4 (ноль можно, но за минусом одной цифры, которая уже использована, т. к. повторов быть не должно) , в качестве единиц - 3 (за минусом двух цифр, которые уже использованы) . Значит, 4·4·3 = 48.

б) Есть пять цифр - 0, 1, 2, 3, 4. В качестве сотен можно использовать только 4 цифры (без нуля, в противном случае число не будет трехзначным) , в качестве десятков - 5 , в качестве единиц – тоже 5 . Значит, 4·5·5 = 100.

в) Чётные числа - это те числа, которые без остатка делятся на 2. Трёхзначные числа - это те числа, которые состоят из 3-х цифр. Из данных цифр чётные числа смогут оканчиваться только на 0, 2 или 4. На месте сотен могут стоять любые цифры, кроме 0 (4 варианта). На месте десяток могут стоять любые цифры (5 варианта). На месте единиц могут стоять только 0, 2 или 4 (3 варианта). Значит, 4·5·3 = 60.

г) На 5 здесь делятся только числа, оканчивающиеся на 0. На месте сотен могут стоять любые цифры, кроме 0 (4 варианта). На месте десяток могут стоять тоже 4 цифры (ноль можно, но за минусом одной цифры, которая уже использована, т. к. повторов быть не должно). На месте единиц может стоять только 0 (1 вариант). Значит, 4·4·1 = 16.

8. 4 пианиста, 5 скрипачей и 8 баянистов участвуют в конкурсе. Сколькими способами жюри может отобрать по 3 победителя в каждой номинации?

● N= 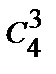· · 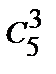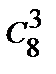= 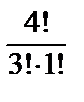· · 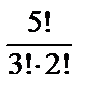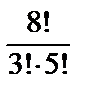= 4·10·56 = 2240.

9. В классе изучается 7 предметов. Сколькими способами можно составить расписание на понедельник, если в этот день должно быть 5 различных предметов?

● Это задача на размещения. Надо разместить 7 предметов на 5 местах (важен порядок).

N= 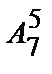= = 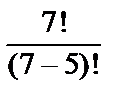= 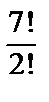7·6·5·4·3 = 2520.

Если решать «в лоб»: На 1-е место можно поставить один из 7 предметов, на 2-е – один из оставшихся 6 предметов,

на 3-е – один из оставшихся 5 предметов, на 4-е – один из оставшихся 4 предметов, на 5-е – один из оставшихся 3 предметов. Т.о., N= 7·6·5·4·3 = 2520.

10. Сколько различных комбинаций из 6 карт содержат 3 дамы, 2 короля и 1 туз?

● Суть задачи: на руках 6 карт: 3 дамы, 2 короля и 1 туз. В колоде по 4 дамы, короля и туза (пики, трефы, бубны, черви). Значит, искомых комбинаций N= 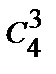· · 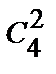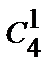= 4·2·3·4 = 96.

11. В футбольной команде имеется 13 полевых игроков и 2 вратаря. Сколькими способами можно выбрать играющий состав, состоящий из 10 игроков 1-го вратаря?

● N= 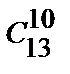· 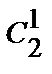= ·2 = 13·2·11·2 = 572.

Задачи для самостоятельного решения

1. В группе 25 студентов. Сколькими способами можно выбрать трех дежурных?

2. Автомобильный номер состоит из четырех цифр, не обязательно различных. Сколько таких номеров можно составить?

3. Сколько можно придумать семизначных телефонных номеров?

4. Сколько вариантов расстановки семи книг на полке можно придумать так, чтобы три определенные книги стояли рядом?

5. Буквы азбуки Морзе состоят их двух символов: точек и тире. Сколько букв можно изобразить, если потребовать, чтобы каждая буква содержала не более пяти символов?

6. Лифт останавливается на десяти этажах. Сколькими способами могут распределиться между этими остановками 8 пассажиров, находящихся в кабине лифта?

7. Сколько 5-значных четных чисел можно составить из цифр 0, 1, 2, 3, 4 (а: всего; б: только из этого набора)?

8. 28 костей домино распределены между 4-мя игроками. Сколько возможно различных распределений?

Дата добавления: 2018-04-15; просмотров: 8681; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!