Пряма і обернена геодезична задача.
Тема 9. Обробка матеріалів теодолітного знімання.
План
1. Плоскі прямокутні координати.
2. Пряма і обернена геодезична задача.
3. Ув’язка замкнутого теодолітного ходу.
4. Складання і оформлення плану теодолітної зйомки.
Плоскі прямокутні координати.
Координатними площинами, відносно яких визначають положення точок на земній поверхні, є площина екватора земного еліпсоїда та площина початкового меридіана.
Координати – це величини, що визначають положення будь-якої точки на поверхні або в просторі відносно прийнятої системи координат.
Система координат встановлює початкові (вихідні) точки поверхні або лінії відліку потрібних величин – початок відліку координат та одиниці їх обчислення.
У геодезії найбільшого застосування набули системи географічних, плоских прямокутних та полярних координат.

Рис. 1.1. Система плоскихкоординат
Плоскими прямокутними геодезичними координатами (прямокутними координатами)називають лінійні величини – абсцису і ординату, що визначають положення точки на площині відносно вихідних напрямків. Вихідними напрямками служать дві взаємно перпендикулярні лінії (рис. 1.1) з початком відліку в точці їх перетину О. Пряма XX є віссю абсцис, а пряма YY – віссю ординат. У цій системі положення будь-якої точки на площині визначається найкоротшою відстанню до неї від осей координат. Так, положення точки А визначається довжиною перпендикулярів ха та уа.Відрізок ханазивають абсцисою, а уа, – ординатою точки А. Відображаються абсциси і ординати в лінійних величинах (найчастіше в метрах).
|
|
|
У геодезії прийнято праву систему прямокутних координат: це відрізняє її від лівої системи координат, яка використовується в математиці. Чверті системи координат, назви яких відповідають назвам сторін світу, нумеруються за годинниковою стрілкою (див. рис. 1.1).У такій системі спрощується вимірювання кутів орієнтування. Абсциси точок, розташованих вверх від початку координат, вважають додатними, а вниз – від’ємними; ординати точок, розташованих праворуч від початку координат, вважають додатними, а ліворуч – від’ємними (табл. 1).
Систему плоских прямокутних застосовують для визначення координат точок на порівняно невеликих ділянках земної поверхні, що приймаються за площину.
Таблиця 1
| Чвертні системи | Координати | |
| X | Y | |
| І – північний схід (Пн.Сх.) | + | + |
| ІІ – південний схід (Пд.Сх.) | – | + |
| ІІІ – південний захід (Пд.Зх.) | – | – |
| IV – північний захід (Пн.Зх.) | + | – |
У державній системі координат за вісь ординат приймають лінію екватора, за вісь абсцис – напрямок меридіана, який називають осьовим (він збігається з напрямком однієї з осей системи прямокутних координат). При виконанні робіт на значних за розмірами територіях осьовими вибирають кілька меридіанів. Для невеликих ділянок початок відліку координат може бути в будь-якій точці ділянки (це так звана система з умовним початком координат).
|
|
|
Координати, початком відліку яких є певна точка на місцевості, називають топоцентричними. Якщо на горизонтальній площині через довільно вибрану точку О провести пряму ОХ (так звана полярна вісь), то положення будь-якої точки, наприклад М, визначатиметься радіусом – вектором r1 та кутом напрямку α1, а точка N – відповідно r1і α1 (рис.4.3). Такі координати називають полярними. Кутиα1іα2 вимірюють від полярної осі за ходом годинникової стрілки до радіуса-вектора. Полярна вісь на площині може розташовуватись довільно або збігатися з напрямком меридіана, що проходить через полюс (точка О).
Система плоских прямокутних координат Гаусса-Крюгера.Дану систему координат використовують при великомасштабному зображенні значних частин земної поверхні на площині, отже, і при вирішенні більшості завдань, що зв’язані з проектуванням будівельних комплексів.
|
|
|
Для великомасштабного картографування необхідна проекція, що забезпечує збереження подібного зображення фігур (контурів) при переході з поверхні кулі на площину, спотворення розмірів фігур, що виникають при цьому, мають бути малі і легко враховуватися. Даним вимогам відповідає прийнята з 1928 р. поперечно-циліндрична рівнокутна проекція Гаусса-Крюгера.

Рис. 1.2. Схема побудови поперечної циліндричної проекції
Зображення поверхні земної кулі на площині в проекції Гаусса-Крюгера отримують наступним чином. Поверхню розбивають меридіанами на зони шириною 3˚ або 6˚ за довготою. Земну кулю вписують в циліндр так, щоб площина екватора співпала з віссю циліндра (рис. 1.2). Кожна зона з центру Землі проектується на бічну поверхню циліндра. Після проектування бічну поверхню циліндра розгортають в площину, розрізавши її по меридіанах, що проходять через земні полюси. На отриманому зображенні середні (осьові) меридіани зон (рис. 4.5) і екватор – прямі лінії, всі інші меридіани і паралелі – криві. Спотворення розмірів контурів поблизу середніх (осьових) меридіанів зон мінімальні і зростають у міру віддалення до країв. Лінія на поверхні кулі завдовжки Sпри зображенні її на площині отримає спотворення
|
|
|
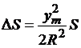 ,
,
Де уm = (у1 + у2)/2 – середнє значення ординат початкової у1 і кінцевої у2 точок лінії; R – радіус Землі.
Відносні спотворення ΔS/Sна краях шестиградусної зони можуть досягати величини порядку 1/1500, а трьохградусної – порядку 1/6000. Вибір ширини зони (6˚ або 3˚) залежить від того, з якою точністю повинно вестися проектування будівельного комплексу. Якщо для проектування потрібні топографічні матеріали масштабу 1:10 000 і дрібніше, застосовують шестиградусні зони, для карт масштабу 1:5000 крупніших масштабів – трьохградусні. Весь земний еліпсоїд охоплюють 60 шестиградусних зон. Вони нумеруються арабськими цифрами, починаючи від Грінвинчського меридіану на схід.
За початок відліку координат в кожній зоні приймають точку перетину осьового меридіана – осі абсцис Хі екватора – осі ординат Y. На картах проводять прямокутну координатну сітку, що складається з прямих ліній, паралельних осьовому меридіану і екватору (рис. 1.3). Відстані між суміжними лініями сітки для масштабів карт 1:10 000; 1:25 000 і 1:50 000 складають один кілометр на місцевості.
ΔS =S

Рис.1.3. Шестиградусні зони Гаусса-Крюгера
Система координат в кожній зоні однакова. Для території України, що розташована в північній півкулі, абсциси завжди позитивні. Що стосується ординат, то вони в кожній зоні могли б бути як позитивними так і негативними. Для того, щоб і ординати були завжди позитивні, початок координат домовились змістити на захід на 500 км. В цьому випадку всі точки на схід і захід від осьового меридіана матимуть позитивні ординати. Такі ординати називаються перетвореними. Перетворена ордината починається з номера зони. Наприклад, якщо точка розташована в четвертій зоні на відстані 64 245 м на захід від осьового меридіана, її перетворена ордината рівна 4 435 755 м, якщо на тій же відстані на схід від того ж осьового меридіана, то перетворена ордината y= 4 564 245 м.

Рис. 1.4. Координатна сітка
Усі сучасні топографічні карти України складені у проекції Гаусса-Крюгера. В інженерній практиці для невеликих ділянок місцевості план може бути складений в умовній системі прямокутних координат. Початок умовної системи координат вибирають так, щоб значення Xта Yбули додатними. Вісь абсцис орієнтують у напрямку магнітного меридіана.
Для зручності визначення прямокутних координат на планах і картах нанесена координатна сітка (рис. 1.4). Це система взаємно перпендикулярних ліній, проведена через певні відстані паралельно осям Xта Yзони. Значення абсцис Xта умовних ординат Yліній координатної сітки підписані на картах і планах.
Пряма і обернена геодезична задача.
Пряма геодезична задача. При прокладанні полігонів та вирішенні інших інженерно-геодезичних задач потрібно передати координати з одних точок на інші. Якщо відомо координати однієї точки і потрібно визначити координати іншої, то для вирішення задачі знімають горизонтальну відстань між точками і дирекцій ний кут. Такий процес називають прямою геодезичною задачею.
Пряма геодезична задача полягає у визначенні координат кінцевої точки лінії за довжиною її горизонтального прокладання, напрямком та координатами початкової точки.

Рис. 2.1. Пряма та обернена геодезичні задачі
Так, якщо взяти точку А (рис. 2.1) за полюс полярної системи координат, а пряму АС – за полярну вісь, паралельну осі ОХ,то полярними координатами точки В будуть вектор S і кут напрямку α. Потрібно обчислити прямокутні координати цієї точки в системі ХО. На рисунку видно, що хВ відрізняється від хА на величину (хВ - хА) = Δх, а уВ відрізняється від уА на величину (уВ - уА) = Δу. Різниці координат кінцевої (В) і початкової (А) точок лінії АВ ΔхіΔуназивають приростами координат. З рисунка видно, що приростами координат лінії АВ є її ортогональні проекції на координатній осі, а координати ХВ і УВ можуть бути обчислені за формулами:
ХВ = ХА + ΔхАВ; УВ = УА + ΔуАВ 2.1
Значення приростів визначаються з прямокутника АВС за заданими S і α, оскільки прирости Δх і Δу є катетами цього прямокутного трикутника:
ΔхАВ = S × соsα; ΔуАВ = S × sіnα 2.2
Прирости координат мають різні знаки. Знак приростів залежить від знака косинуса і синуса кута напрямку або від назви чверті прямокутної системи координат (табл. 1).
Підставивши значення приростів Δх і Δу у рівняння (2.1), одержимо формули для розв’язання прямої геодезичної задачі:
ХВ = ХА + S × соsα; УВ = УА + S × sіnα 2.3
Обернена геодезична задача. Її вирішують під час прив’язки полігонів до опорних пунктів геодезичної мережі, при будівництві тунелів, метрополітену, інших інженерних споруд.
Обернена геодезична задача полягає у визначенні довжини горизонтального прокладення і кута напрямку лінії за відомими координатами її початкової і кінцевої точок.
Кут напрямку можна визначити, обчисливши його тангенс за катетами прямокутного трикутника (рис. 2.1):
tgα =  2.4
2.4
Горизонтальне прокладання S, згідно з формулою (2.2), можна визначити за двома формулами:
S = 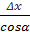 =
= 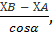 S =
S =  =
=  2.5
2.5
Обернену задачу можна розв’язати в такій послідовності: спочатку обчислити горизонтальне прокладанняSза теоремою Піфагора:
 , 2.6
, 2.6
а потім обчислити кут напрямкуαза формулами, згідно з (2.5).
Дата добавления: 2018-04-15; просмотров: 288; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
