Интегрирование рациональных дробей
Тема: Интегрирование функций различными методами.
Основные понятия.
Определение. Функция 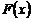 называется первообразной функции
называется первообразной функции  на интервале
на интервале  , если для любого
, если для любого 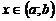 выполняется равенство
выполняется равенство
 .
.
Определение. Совокупность всех первообразных функций  +С для функции
+С для функции  называется неопределенным интегралом функции
называется неопределенным интегралом функции 

Свойства неопределенного интеграла.
1. Постоянный множитель можно выносить за знак интеграла
 ,
,  - число
- число
2. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых функций

Таблица основных интегралов
1. 
| 10. 
|
2. 
| 11. 
|
3. 
| 12. 
|
4. 
| 13. 
|
5. 
| 14. 
|
6. 
| 15. 
|
7. 
| 16. 
|
8. 
| 17. 
|
9. 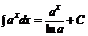
| 18. 
|
Метод непосредственного интегрирования.
При непосредственном интегрировании применяют:
- тождественные преобразования подынтегральной функции  ;
;
- свойства неопределенного интеграла;
- таблицу основных интегралов.
Пример 2.1. Найти интеграл  .
.

= 
Пример 2.2. Найти интеграл  .
.

Интегрирование по формуле линейной замены
Если 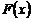 первообразная для
первообразная для  , то
, то  первообразная для
первообразная для  .
.
 , a, b – числа
, a, b – числа
Пример 3.1. Найти интеграл 
Рассмотрим подынтегральную функцию  .
.
Аргументом синуса является линейная функция:
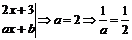

Пример 3.2. Найти интеграл  .
.
линейная функция:  или
или 

Интегрирование методом замены переменной (или подстановкой)
|
|
|
Метод применяется, если под знаком интеграла произведение (частное) двух функций. Причём:
одна функция является производной другой функции, или
одна функция является производной от внутренней функции другой.
Формула интегрирования подстановкой

Пример 4.1. Найти интеграл  .
.
Под знаком интеграла произведение двух функций  и
и  .
.
Причём 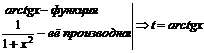
Тогда  .
.
Таким образом, получаем интеграл от новой переменной  :
:

Вернемся к прежней переменной, для этого заменим  на
на  , получим:
, получим:  - ответ.
- ответ.
Запись: 
Пример 4.2. Найти интеграл 
Под знаком интеграла произведение двух функций  и
и  . Причём второй множитель
. Причём второй множитель  является сложной функцией, где показательная функция – внешняя функция, а
является сложной функцией, где показательная функция – внешняя функция, а  - внутренняя функция. Заметим, что производная внутренней функции
- внутренняя функция. Заметим, что производная внутренней функции
 .
.
Тогда эту внутреннюю функцию обозначим за новую переменную
 .
.
Найдем  .
.
Таким образом получаем интеграл от новой переменной  :
:

5. Метод интегрирования по частям.
Нахождение интеграла по формуле
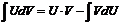 ,
,
называется интегрированием по частям.
Формула показывает, что вычисление интеграла  сводится к вычислению интеграла
сводится к вычислению интеграла  , который должен оказаться более простым или даже табличным.
, который должен оказаться более простым или даже табличным.
Суть метода:
- подынтегральное выражение представляют в виде произведения двух сомножителей  и
и  ;
;
|
|
|
- находят  и
и  ;
;
- применяют формулу интегрирования по частям.
Укажем основные типы интегралов, интегрируемых методом по частям.
I) В интегралах типа 
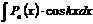
 ,
,

где  - многочлен n-ой степени, k – const.
- многочлен n-ой степени, k – const.
Обозначим  ,
,
dV - оставшееся выражение 
 .
.
Тогда 

Если степень многочлена n > 1, то интегрирование по частям применяют последовательно несколько раз.
Пример 5.1. Найти интеграл 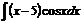 .
.

Пример 5.2. Найти интеграл  .
.

II) В интегралах типа 

где  - многочлен n-ой степени, k – const.
- многочлен n-ой степени, k – const.
Обозначим  ,
,
U - оставшаяся функция  (или
(или  , или
, или  , или
, или  , или
, или  ).
).
Тогда  ,
,
 .
.
Пример 5.4. Найти интеграл  .
.


Пример 5.5. Найти интеграл  .
.

Интегрирование рациональных дробей
Дробно-рациональной функцией (рациональной дробью)  называется отношение двух многочленов с действительными коэффициентами, т.е.
называется отношение двух многочленов с действительными коэффициентами, т.е.  , где
, где  - степени многочленов.
- степени многочленов.
Если  , то дробь правильная.
, то дробь правильная.
Если  , то дробь неправильная.
, то дробь неправильная.
Всякую неправильную дробь  можно путем деления числителя на знаменатель, представить в виде суммы многочлена
можно путем деления числителя на знаменатель, представить в виде суммы многочлена  и правильной остаточной дроби
и правильной остаточной дроби  ,
,  , т.е.
, т.е.  .
.
|
|
|
Пример 6.1. Представить рациональную дробь  в виде суммы многочлена и правильной дроби
в виде суммы многочлена и правильной дроби
 - неправильная рациональная дробь, т.к. степень числителя (
- неправильная рациональная дробь, т.к. степень числителя (  ) больше степени знаменателя (
) больше степени знаменателя (  ).
).
Разделим числитель на знаменатель. При этом многочлены запишем по убыванию степеней, а степени отсутствующие в явном виде с нулевыми коэффициентами.







 - целая часть
- целая часть





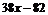 - остаток
- остаток
тогда  .
.
Интегрирование рациональных дробей сводится к интегрированию соответствующих простейших дробей. Простейшими дробями называются дроби следующих 3-х типов:
 - I тип
- I тип
 , где
, где  , - II тип
, - II тип
 , где дискриминант знаменателя отрицательный, - III тип
, где дискриминант знаменателя отрицательный, - III тип
Рассмотрим интегрирование простейших рациональных дробей на примерах.
Пример 6.2. Интегрирование простейшей рациональной дроби I типа.

Пример 6.3. Интегрирование простейшей рациональной дроби II типа.
 .
.
Пример 6.4. Интегрирование простейшей рациональной дроби III типа.

1. Найдем дискриминант знаменателя 
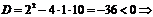 дробь III типа.
дробь III типа.
2. Выделим в знаменателе полный квадрат.

3. Введем замену: основание выделенного квадрата принимаем за новую переменную.
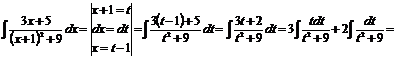 I-й интеграл берется методом замены, а II-й – табличный
I-й интеграл берется методом замены, а II-й – табличный
|
|
|

4. Возвращаемся к прежним переменным

Рассмотрим общее правило интегрирования рациональных дробей.
Чтобы проинтегрировать рациональную дробь, необходимо:
а) Если дробь неправильная, то выделить целую часть и остаточную правильную рациональную дробь;
б) разложить знаменатель правильной рациональной дроби на линейные и квадратичные множители (если это необходимо), при этом возможны следующие типы множителей:
 - линейный,
- линейный,
 - линейный кратности “k”,
- линейный кратности “k”,
 - квадратичный;
- квадратичный;
в) разложить правильную дробь на сумму простейших, при этом:
множителю  соответствует простейшая рациональная дробь I типа
соответствует простейшая рациональная дробь I типа 
множителю  соответствует разложение (сумма дробей I и II типов)
соответствует разложение (сумма дробей I и II типов) 
множителю  соответствует дробь III типа
соответствует дробь III типа  ;
;
г) привести обе части равенства к общему знаменателю и приравнять числители;
д) найти неопределенные коэффициенты;
е) проинтегрировать каждую из полученных дробей и выделенную целую часть.
Методы нахождения неопределенных коэффициентов рассмотрим на примерах.
Пример 6.5. Найти интеграл 
 - правильная рациональная дробь.
- правильная рациональная дробь.
Разложим знаменатель  на множители по формуле
на множители по формуле  , где
, где  - корни квадратного трехчлена.
- корни квадратного трехчлена.

тогда  .
.
Представим подынтегральную дробь в виде суммы простейших дробей. Линейным множителям  и
и  знаменателя данной дроби соответствуют простейшие рациональные дроби вида
знаменателя данной дроби соответствуют простейшие рациональные дроби вида
 и
и  .
.
Тогда  .
.
Приведем правую часть равенства к общему знаменателю:
 ,
,
т.к. знаменатели равны, то приравняем числители:
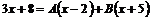 .
.
Коэффициенты 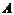 и
и  можно найти одним из способов.
можно найти одним из способов.
I способ (метод сравнивания коэффициентов).


Приравняем коэффициенты при одинаковых степенях x:



Тогда 1 уравнение системы имеет вид 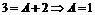 . Таким образом
. Таким образом  .
.
II способ (метод частных решений).

Пусть  , тогда
, тогда 

Пусть  , тогда
, тогда 

Таким образом  .
.
Тогда

Проинтегрируем

Пример 6.6. Найти интеграл 
 - неправильная рациональная дробь.
- неправильная рациональная дробь.
Представим дробь в виде суммы многочлена и правильной дроби (решение см. пример 4.1)
Тогда, 
Разложим знаменатель правильной дроби на множители:



 Решив систему, получаем
Решив систему, получаем 


Пример 6.7. Найти интеграл 
 - правильная рациональная дробь, так как степень числителя – 2, а знаменателя – 3.
- правильная рациональная дробь, так как степень числителя – 2, а знаменателя – 3.
Знаменатель уже разложен на линейные множители, причем множитель  имеет кратность 2.
имеет кратность 2.
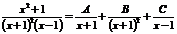


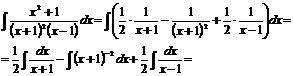

Дата добавления: 2018-04-15; просмотров: 382; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
