Статистический подход к понятию вероятности.

Прочитайте весь тексти запишите в тетрадь текст выделенный подчеркиванием. Лекция: Теория вероятностей.

Введение

В новые российские образовательные стандарты по математике включено обязательное изучение элементов теории вероятностей и статистики.Этот материал необходим прежде всего для формирования функциональной грамотности — умений воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, проводить простейшие вероятностные расчеты.

Кроме того, изучение теории вероятностей и статистики имеет свою специфику подразумевающую проведение реальных экспериментов, требующих больших затрат времени, статистическую обработку больших массивов данных и т.д., которая требует иных, помимо традиционных, форм организации учебной деятельности.

Вероятностно-статистическиеметоды могут и должны быть использованы не только на уроках математики, но и на занятиях по другим предметам (информатика, биология, физика, экономика и др.).

Именно по этим причинам следует уделить особое внимание изучению данного раздела математики.

2.Случайные события и вероятность.

2.1. Понятие о случайном опыте и случайном событии.

Опыт, эксперимент, наблюдение явления называются испытаниями.

Примерами испытаний являются: бросание монеты, извлечение шара из урны, бросание игральной кости.

Результат, исход испытания называются событием.

Событиями являются: выпадение герба или решки, взятие белого или черного шара, появление того или иного числа очков на брошенной игральной кости. События обозначаются большими буквами латинского алфавита A, B, C,... Любое событие происходит вследствие испытания.

Случайным событием называется событие, которое может произойти или не произойти во время данного испытания.

Например, событие — выпадение шести очков при бросании игральной кости — случайное. Оно может и не наступить в данном испытании. Можно привести другие примеры случайных событий: вынимая наугад одну карту из колоды, вы взяли туз; стреляя, стрелок попадает в цель.

Достоверным событием называется событие, которое вследствие данного испытания обязательно произойдет.

Невозможным событием называется такое событие, которое вследствие данного испытания не может произойти.

Например, испытание: извлечение шара из урны, в которой все шары белые. Событие А - вынут белый шар - достоверное; событие В - вынут черный шар –невозможное.

Два события называются совместимыми (совместными), если появление одного из них не исключает появление другого в одном и том же испытании.

Рассмотрим такой пример. Испытание: однократное бросание игральной кости. Событие А- появление четырех очков. Событие В- появление четного числа очков. События А и B - совместимые.

Два события называются несовместимыми (несовместными), если появление одного из них исключает появление другого в одном и том же испытании.

Пример. Испытание: однократное бросание игральной кости. Пусть события А₁, А₂, А₃, А₄, А₅,А₆-соответственно выпадение одного очка, двух, трех, четырех, пяти, шести. Эти события являются несовместимыми.

Два событияА и 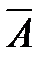называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит.

Пример. Испытание: бросание монеты. СобытиеА — выпадение герба, событие 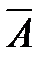- выпадение решки.

Несколько событий образуют полную группу событий в данном испытании, если в результате этого испытания обязательно наступит хотя бы одно и только одно из них.

Пример. Стрелок произвел выстрел по цели. Обязательно произойдет одно из следующих двух событий: попадание, промах, осечка. Никакое другое событие произойти не может. Следовательно, эти три несовместных события образуют полную группу.

Равновозможные события — это такие события, каждое из которых не имеет никаких преимуществ в появлении чаще другого во время многочисленных испытаний, которые проводятся с одинаковыми условиями.

Пример. Появление «герба» и появление «решки» при бросании монеты — равновозможные события. Действительно, предполагается, что монета изготовлена из однородного материала, имеет правильную форму и наличие чеканки не оказывает влияния на выпадение той или иной стороны монеты.

2.2.Частота случайного события.

Статистический подход к понятию вероятности.

Поставим перед собой вопрос: можно ли вычислить вероятность события с помощью ряда экспериментов?

Для каждого из нас очевидно, что, например, вероятность попасть под дождь в Лондоне гораздо выше, чем в пустыне Сахара.

Весь наш жизненный опыт подсказывает, что любое событие считается тем более вероятным, чем чаще оно происходит. Значит, вероятность должна быть каким-то образом связана с частотой появления события.

1. Частота случайного события.

Относительной частотой (или статистической частотой) случайного события называют отношение числа появлений этого события к общему числу проведенных экспериментов:

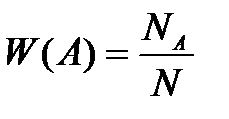
где А – случайное событие.

Nраз проведено испытание и при этом событие А наступило в N_Аслучаях.

Пример. Наблюдения показывают, что в среднем среди 1000 новорожденных детей 515 мальчиков. Частота рождения мальчика в такой серии наблюдений равна 0,515:

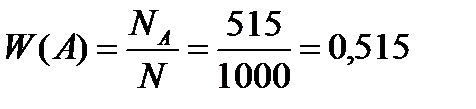
Пример. Для выяснения качества семян было отобрано и высеяно в лабораторных условиях 1000 штук. 980 семян взошли. Найдите частоту нормальной всхожести семян.

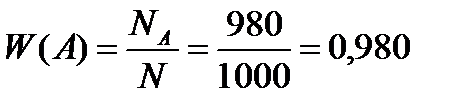
Может быть, относительную частоту и нужно принять за вероятность?

К сожалению, такое определение приводит к одному неудобству – значение частоты зависит от конкретной серии опытов и от их количества.

Фундаментальным свойством относительных частот (если хотите – законом природы) является тот факт, что с увеличением числа опытов относительная частота случайного события постепенно стабилизируется и приближается к вполне определенному числу, которое и следует считать его вероятностью.

Пример. Подбрасывание монеты.

Теоретическая (классическая) вероятность: всего 2 равновозможныхисхода: выпадения герба или выпадение цифры. Вероятность выпадения герба(1 исход) равна 0,5.

Французский естествоиспытатель Бюффон (XVIIIв.) бросил монету 4040 раз, и при этом герб выпал в 2048 случаях. Следовательно, частота выпадения герба в данной серии испытаний равна: 0,50629...

Английский математик Карл Пирсон (1857-1936) бросал монету 24000 раз, причем герб выпал 12012 раз. Следовательно, частота выпадения герба в данной серии испытаний равна:0,505...

Данный пример подтверждает естественное предположение о том, что вероятность выпадения герба при одном бросании монеты равна 0,5.

2.3.Классическое определение вероятности события.

Вероятности элементарных событий договорились обозначать буквой Р латинского алфавита по начальной букве латинского слова «probabilitas», что и означает вероятность.

Вероятность случайного события — это отношение числа событий, которые благоприятствуют этому событию, к общему числу всех равновозможных несовместимых событий:

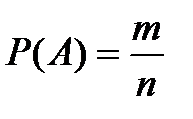где A — событие;

P(A) — вероятность события;

n — общее число равновозможных и несовместных событий;

m — число событий, которые благоприятствующих появлению события A.

Это — классическое определение вероятности случайного события.

Отметим следующие свойства вероятности события:

1. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Так как число событий, благоприятствующих событию A, может принимать значения от 0 до n, то вероятность случайного события может принимать значения

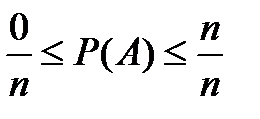
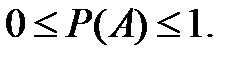
2. Вероятность достоверного события равна 1.

Действительно, если событие является достоверным, то оно обязательно произойдет. В этом случае m= n и тогда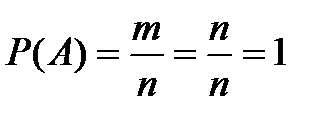

3. Вероятность невозможного события равна 0.

Для невозможного события число благоприятствующих исходов m равно 0 и, следовательно,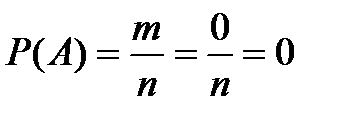

Пример. Найти вероятность выпадения шести очков при одном бросании игральной кости.

Решение: m=1, n=6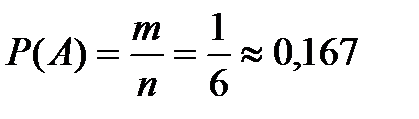

Ответ: 0,167.

Пример. Какова вероятность появления четного числа очков (событие А) при одном бросании игрального кубика?

Решение: Рассмотрим события А_i – выпало i очков, i= 1, 2, …,6. Очевидно, что эти события образуют полную группу событий. Тогда число всех случаев n = 6. Выпадению четного числа очков благоприятствуют случаи А₂, А₄, А₆, т.е. m= 3. Тогда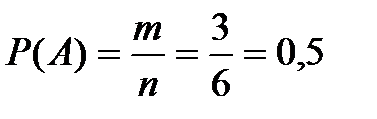

Ответ: 0,5.

Пример. В коробке лежат 3 карандаша: синий, зеленый и красный. Дима наугад вынимает два карандаша. Какова вероятность того, что это будут синий и красный карандаши?

Решение: Равновозможные исходы: СЗ, СК, ЗС, ЗК, КС, КЗ. Благоприятствующие исходы: СК, КС.

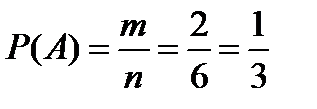
Ответ: 1/3.

Пример. Галя дважды бросила игральный кубик. Известно, что в сумме у нее выпало 9 очков. Найдите вероятность того, что при втором броске выпало 6 очков.

Решение: Равновозможные исходы: 3+6, 6+3, 4+5, 5+4. Благоприятствующие исходы: 3+6.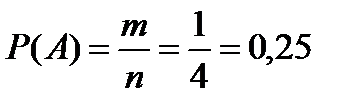

Ответ: 0,25.

3.Теоремы о вероятностях событий.

3.1. Произведение вероятностей независимых событий

Произведением двух событийА и В называется событие А×В, состоящее в совместном появлении этих событий.

СобытиеВ называется независящим от события А, если вероятность события В не зависит от того, произошло или не произошло событие А.

Теорема. Вероятность совместного наступления двух независимых событийА и В равна произведению вероятностей этих событий

Р(АВ) = Р(А) × Р(В).

Пример. Два стрелка одновременно стреляют в цель. Вероятность попадания для первого стрелка равна 0,8, для второго – 0,6. Нужно найти вероятность того, что оба стрелка попадут в цель.

Решение

События: А-«Попал в цель первый стрелок» и В-« Попал в цель второй стрелок» являются независимыми. Нужно определить вероятность их совместного наступления.

Р(А)=0,8

Р(В)=0,6

Р(АВ) = Р(А) · Р(В)=0,8·0,6=0,48.

Ответ: 0,48.

3.2.Произведение вероятностей зависимых событий

СобытиеВ называется зависящим от события А, если вероятность события В зависит от того, произошло или не произошло событие А.

Вероятность наступления события В при условии, что событие А уже произошло, называется условной вероятностью и обозначается символом Р_А(В).

Теорема.Вероятность совместного наступления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже произошло:Р(АВ) = Р(А) · Р_А(В).

Теорема умножения легко обобщается на любое конечное число событий. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже произошли.

Пример. В урне находятся 2 белых и 4 черных шара. Найти вероятность того, а) что вынутые подряд два шара окажутся белыми; б) первый шар окажется белым, а второй – черным.

Решение: а) Событие А – «Первый шар – белый», событие В –«Второй шар – белый».

Р(А)=2/6=1/3

Р_А(В)=1/5

Р(АВ)= Р(А) · Р_А(В)=1/15≈0,067.

б)Событие С – «Первый шар – белый», событие D –«Второй шар – белый».

Р(С)=2/6=1/3

Р_С(D)=4/5

Р(CD)= Р(C) · Р_С(D)=4/15≈0,267.

Ответ: а) 0,067; б) 0,267.

3.3.Сумма вероятностей несовместных событий.

Рассмотрим два несовместных события А и В. Допустим, нас интересует ситуация, когда произойдет одно из этих событий либо А, либо В. Такое событие называется суммой событий А и В и обозначается: А+В. Вероятность события обозначается Р(А+В).

Например, в пенале у Пети лежат три ручки: красного (К), синего (С) и черного (Ч) цветов. Петя наугад достает одну ручку. Чтобы написать контрольную работу, ему нужно достать ручку черного или синего цвета. Вполне логично предположить, что вероятность достать ручку нужного цвета Р(С+Ч) будет равна сумме вероятностейР(С)+Р(Ч).

Действительно, имеет место следующая теорема.

Теорема. Вероятность наступления одного из двух несовместных событий равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В).

Замечание. Данная теорема справедлива для любого числа попарно несовместных событий.

Теорема. Вероятность наступления одного из n попарно несовместных событий равна сумме вероятностей этих событий: Р(А₁+А₂+…+А_n)=Р(А₁)+Р(A₂)+…+P(A_n).

Пример. В пакете лежат 10 конфет «Мишка косолапый», 12 конфет «Вдохновение» и 8 батончиков «Сникерс». Лиза наугад достает одну конфету. Найти вероятность того, что это будет «Мишка косолапый» или «Вдохновение».

Решение: Обозначим события: М- достали «Мишка косолапый»; В - «Вдохновение»; С - «Сникерс». Р(М)=10/30=1/3; Р(В)=12/30=2/5; Р(С)=8/30=4/15.

Р(М+В)=Р(М)+Р(В)=1/3+2/5=11/15.

Ответ: 11/15.

Пример. В шахматной партии, которую Остап Бендер играет с любителем шахмат города Васюки, вероятность выигрыша Остапа равна 0,001, вероятность ничьей равна 0,01. Найдем вероятность события А «Остап не проиграл».

Решение: Для того, чтобы произошло событие «Остап не проиграл», должно произойти либо событие А: «Остап выиграл» либо событие В: «Остап сыграл вничью».Данные события являются несовместными и, следовательно, Р(А+В) = 0,001 +0,01 = 0,011.

Ответ: 0,011.

Дата добавления: 2018-04-15; просмотров: 2126; Мы поможем в написании вашей работы!
Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!