Необходимо и достаточное условие существования решения системы линейных уравнений. Методы решения
Рассмотрим систему линейных уравнений с квадратной матрицей вида:
A`Х =`В (4.12)
Теоретически необходимым и достаточным условием существования единственного решения системы (4.12) является условие:
det(A)¹0. (4.13)
Если det(A)=0, то матрица А называется вырожденной, а система линейных уравнений либо не имеет решения, либо имеет их бесчисленное множество. При выполнении практических расчетов на ЭВМ из-за округления результатов вычислений точное равенство определителя, как правило, не выполняется. Поэтому вместо условия (4.12) необходимо использовать условие вида:
½det(A) ½³ e >0, (4.14)
в котором e > 0 - малое число, учитывающее возможные погрешности вычислений.
Методы решения систем линейных алгебраических уравнений делятся на две большие группы – прямые (точные) и итерационные.
Прямые методы используют либо определенные соотношения (формулы) для вычисления неизвестных либо алгоритмы, в которых точно определены все действия. При этом решение получается после выполнения заранее известного количества арифметических операций. Эти методы сравнительно просты и наиболее универсальны, т.е. пригодны для решения широкого класса систем линейных уравнений. В тоже время прямые методы имеют и ряд недостатков. Как правило, они требуют хранения в оперативной памяти сразу всей матрицы, и при больших значениях n расходуется много места в памяти компьютера. Кроме этого более существенным недостатком прямых методов является накапливание погрешностей в процессе решения, поскольку вычисления на любом этапе используют результаты предыдущих операций. Второе название прямых методов - точные выражает тот факт, что решение выражается в виде точных формул через коэффициенты системы. Однако идеальное точное решение может быть получено лишь при точном выполнении вычислений (и, разумеется, при точных коэффициентах системы). На практике же при использовании компьютеров вычисления проводятся с погрешностями. Поэтому неизбежны погрешности и в окончательных результатах, вызванные погрешностями вычислений (например, погрешностью округления).
|
|
|
Итерационные методы позволяют определить искомое решение системы путем выполнения последовательных приближений. Для начала вычислений необходимо задать некоторое приближенное решение – начальное приближение, после чего с помощью заданного алгоритма проводится один цикл вычислений, называемый итерацией. В результате итерации находят новое приближение. Итерации проводят до тех пор, пока не будет получено решение с заданной точностью. Важное достоинство итерационных методов состоит в том, что погрешности окончательных результатов не накапливаются, поскольку точность вычислений в каждой итерации определяется лишь результатами предыдущей итерации и практически не зависит от ранее выполненных вычислений.
|
|
|
Вопросы для проверки знаний.
1. Как формулируется теоретический вариант необходимого и достаточного условия существования единственного решения линейной системы ?
2. Как формулируется практическое необходимое и достаточное условие существования единственного решения линейной системы ?
3. На какие два группы делятся методы решения линейных систем ?
4. В чем заключаются преимущества и недостатки прямых методов решения линейных систем ?
5. В чем заключаются преимущества и недостатки итрационных методов решения линейных систем ?
Прямые методы решения систем линейных уравнений
|
|
|
Среди прямых методов решения, в которых решение системы выражено в формульном виде наиболее известными являются методы:
1) с помощью обратной матрицы,
2) метод Крамера.
Метод с использованием обратной матрицы.
Векторное решение системы линейных уравнений вида (4.12) имеет вид:
`Х = A-1`В (4.15)
где A-1 матрица, обратная к А, которая при умножении на нее дает в итоге единичную матрицу Е:
A-1 A = A A-1 = Е.
Таким образом, решение системы сводится к решению задачи обращения квадратной матрицы системы А.
Квадратная матрица А обратима тогда и только тогда, когда она невырожденная, то есть её определитель det(A) не равен нулю.
Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться как прямыми , так и итерационными способами.
[править] Метод Гаусса—Жордана
Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A−1.
|
|
|
При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λi (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):
 .
.
 .
.
Вторая матрица после применения всех операций станет равна Λ, то есть будет искомой. Сложность алгоритма — O(n3).
[править] С помощью матрицы алгебраических дополнений

CT — транспонированная матрица алгебраических дополнений;
Полученная матрица A−1 и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя Odet и равна O(n²)·Odet.
Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.
[править] Использование LU/LUP-разложения
Матричное уравнение AX = In для обратной матрицы X можно рассматривать как совокупность n систем вида Ax = b. Обозначим i-ый столбец матрицы X через Xi; тогда AXi = ei,  ,поскольку i-м столбцом матрицы In является единичный вектор ei. другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³)[1].
,поскольку i-м столбцом матрицы In является единичный вектор ei. другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³)[1].
Если матрица A невырождена, то для неё можно рассчитать LUP-разложение PA = LU. Пусть PA = B, B − 1 = D. Тогда из свойств обратной матрицы можно записать: D = U − 1L − 1. Если умножить это равенство на U и L то можно получить два равенства вида UD = L − 1 и DL = U − 1. Первое из этих равенств представляет собой систему из n² линейных уравнений для  из которых известны правые части (из свойств треугольных матриц). Второе представляет также систему из n² линейных уравнений для
из которых известны правые части (из свойств треугольных матриц). Второе представляет также систему из n² линейных уравнений для  из которых известны правые части (также из свойств треугольных матриц). Вместе они представляют собой систему из n² равенств. С помощью этих равенств можно реккурентно определить все n² элементов матрицы D. Тогда из равенства (PA)−1 = A−1P−1 = B−1 = D. получаем равенство A − 1 = DP.
из которых известны правые части (также из свойств треугольных матриц). Вместе они представляют собой систему из n² равенств. С помощью этих равенств можно реккурентно определить все n² элементов матрицы D. Тогда из равенства (PA)−1 = A−1P−1 = B−1 = D. получаем равенство A − 1 = DP.
В случае использования LU-разложения не требуется перестановки столбцов матрицы D но решение может разойтись даже если матрица A невырождена.
Сложность алгоритма — O(n³).
[править] Итерационные методы
[править] Методы Шульца

[править] Оценка погрешности
[править] Выбор начального приближения
Проблема выбора начального приближения  в рассматриваемых здесь процессах итерационного обращения матриц не позволяет относиться к ним как к самостоятельным универсальным методам, конкурирующими с прямыми методами обращения, основанными, например, на LU-разложении матриц. Имеются некоторые рекомендации по выбору
в рассматриваемых здесь процессах итерационного обращения матриц не позволяет относиться к ним как к самостоятельным универсальным методам, конкурирующими с прямыми методами обращения, основанными, например, на LU-разложении матриц. Имеются некоторые рекомендации по выбору  , обеспечивающие выполнение условия
, обеспечивающие выполнение условия 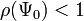 (спектральный радиус матрицы меньше единицы), являющегося необходимым и достаточным для сходимости процесса. Однако при этом, во-первых, требуется знать сверху оценку спектра обращаемой матрицы A либо матрицы
(спектральный радиус матрицы меньше единицы), являющегося необходимым и достаточным для сходимости процесса. Однако при этом, во-первых, требуется знать сверху оценку спектра обращаемой матрицы A либо матрицы  (а именно, если A — симметричная положительно определённая матрица и
(а именно, если A — симметричная положительно определённая матрица и  , то можно взять
, то можно взять 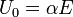 , где
, где  ; если же A — произвольная невырожденная матрица и
; если же A — произвольная невырожденная матрица и  , то полагают
, то полагают  , где также
, где также  ; можно конечно упростить ситуацию и, воспользовавшись тем, что
; можно конечно упростить ситуацию и, воспользовавшись тем, что  , положить
, положить  ). Во-вторых, при таком задании начальной матрицы нет гарантии, что
). Во-вторых, при таком задании начальной матрицы нет гарантии, что  будет малой (возможно, даже окажется
будет малой (возможно, даже окажется  ), и высокий порядок скорости сходимости обнаружится далеко не сразу.
), и высокий порядок скорости сходимости обнаружится далеко не сразу.
[править] Примеры
[править] Матрица 2х2

Обращение матрицы 2х2 возможно только при условии, что  .
.

Рассмотрим квадратную матрицу
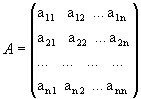 .
.
Обозначим D =det A.
Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если D = 0.
Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.
Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Матрица, обратная матрице А, обозначается через А-1, так что В = А-1. Обратная матрица вычисляется по формуле
 , (4.5)
, (4.5)
где А i j - алгебраические дополнения элементов a i j.
Вычисление обратной матрицы по формуле (4.5) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
Пример 2.10. Для матрицы 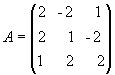 найти обратную.
найти обратную.
Решение. Находим сначала детерминант матрицы А
 значит, обратная матрица существует и мы ее можем найти по формуле:
значит, обратная матрица существует и мы ее можем найти по формуле:  , где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j исходной матрицы.
, где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j исходной матрицы. 

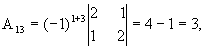






откуда  .
.
Пример 2.11. Методом элементарных преобразований найти обратную матрицу для матрицы: А= 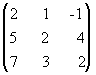 .
.
Решение. Приписываем к исходной матрице справа единичную матрицу того же порядка: 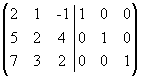 . С помощью элементарных
. С помощью элементарных
преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей.
Для этого поменяем местами первый и второй столбцы: 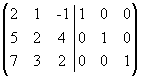 ~
~  . К третьему столбцу прибавим первый, а ко второму - первый, умноженный на -2:
. К третьему столбцу прибавим первый, а ко второму - первый, умноженный на -2:  . Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на 6 второй;
. Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на 6 второй;  . Прибавим третий столбец к первому и второму:
. Прибавим третий столбец к первому и второму:  . Умножим последний столбец на -1:
. Умножим последний столбец на -1: 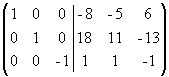 . Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице А. Итак,
. Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице А. Итак,
 .
.
Вводные замечания. Одним из способов решения систем линейных алгебраических уравнений является правило Крамера, согласно которому каждое неизвестное представляется в виде отношения определителей:
 ,
,
где 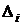 – определитель матрицы, получающейся из матрицы А заменой i-го столбца столбцом правых частей системы (3.1). Определители при этом предлагается вычислять по формулам, рассматриваемым в курсах линейной алгебры, например
– определитель матрицы, получающейся из матрицы А заменой i-го столбца столбцом правых частей системы (3.1). Определители при этом предлагается вычислять по формулам, рассматриваемым в курсах линейной алгебры, например
 . (3.8)
. (3.8)
Здесь индексы a, b, …, w пробегают все возможные  перестановок номеров
перестановок номеров  ; k – число инверсий в данной перестановке.
; k – число инверсий в данной перестановке.
Однако в качестве конкретного метода решения системы (3.1) данные формулы совершенно неприменимы, так как при подсчете каждого определителя по приведенной выше формуле надо вычислить  слагаемых, что нереально при весьма умеренных значениях n. Например, уже при
слагаемых, что нереально при весьма умеренных значениях n. Например, уже при  имеем
имеем  .
.
Очевидно, что сложность системы (3.1) определяется структурой ее матрицы А. Существуют два случая, когда система имеет простые решения. Если А – диагональная матрица
 ,
,
то система (3.1) распадается на n независимый уравнений, каждое их которых содержит одну неизвестную величину, и проблем с вычислениями не возникает.
Просто решается задача и в случае, когда матрица А является треугольной
 .
.
В этом случае из последнего уравнения следует
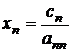 ,
,
и далее
 ,
,
для  .
.
Оценим объем вычислений, связанный с решением системы с треугольной матрицей. Для того, чтобы вычислить 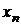 требуется одна операция, для вычисления
требуется одна операция, для вычисления  – три,
– три, 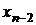 – пять и т.д. Как можно подсчитать, общее число операций при этом равно
– пять и т.д. Как можно подсчитать, общее число операций при этом равно  .
.
Большинство прямых методов решения системы (3.1), используемых на практике, основаны на приведении исходной матрицы к треугольному виду с последующим нахождением неизвестных по рассмотренным выше формулам. Одним из таких методов является метод исключения Гаусса. Другие методы созданы специально для систем, обладающих матрицей определенного вида, например трехдиагональной матрицей. К таким методом относится метод прогонки. Ниже подробно рассматриваются оба этих метода.
Метод Гаусса. Метод исключения Гаусса содержит два этапа: прямой ход – приведение исходной матрицы к треугольному виду путем последовательного исключения неизвестных из уравнений системы и обратный ход – решение системы с треугольной матрицей. Рассмотрим одну из возможных реализаций прямого хода.
Пусть  . Тогда этот элемент называется ведущим или главным. Введем обозначение
. Тогда этот элемент называется ведущим или главным. Введем обозначение  ,
,  .
.
Вычтем последовательно из второго, третьего, …, n-го уравнения системы (3.1) первое уравнение, умноженное соответственно на  ,
, 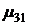 , …,
, …,  . Это позволит обратить в нуль коэффициенты при
. Это позволит обратить в нуль коэффициенты при  во всех уравнениях, кроме первого. В результате получим эквивалентную систему в виде
во всех уравнениях, кроме первого. В результате получим эквивалентную систему в виде
 (3.9)
(3.9)
где  ,
,  ;
; 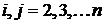 .
.
Теперь исключим неизвестное  из уравнений, начиная с третьего. Пусть
из уравнений, начиная с третьего. Пусть 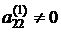 – новый ведущий элемент; положим снова
– новый ведущий элемент; положим снова  ,
, 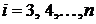 и вычтем из третьего, четвертого, …, n-го уравнения второе уравнение, умноженное соответственно на
и вычтем из третьего, четвертого, …, n-го уравнения второе уравнение, умноженное соответственно на  ,
, 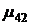 , …,
, …,  . В результате получим
. В результате получим
 (3.10)
(3.10)
где  ,
,  ;
;  .
.
Проделывая описанные действия  раз получим систему уравнений с треугольной матрицей
раз получим систему уравнений с треугольной матрицей
 (3.11)
(3.11)
На этом завершается прямой ход метода Гаусса. Общее количество арифметических операций, которые необходимо совершить для приведения системы к треугольному виду описанным методом, оценивается величиной ~  . Это вполне приемлемая величина (при n ~
. Это вполне приемлемая величина (при n ~ 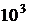 и быстродействии ЭВМ порядка
и быстродействии ЭВМ порядка 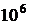 операций в секунду требуемое для расчета время порядка одного часа).
операций в секунду требуемое для расчета время порядка одного часа).
Ø Замечание. В процессе исключения неизвестных приходится выполнять операции деления на коэффициенты 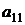 ,
,  и т.д. Поэтому они должны быть отличны от нуля. В противном случае необходимо соответственным образом переставить уравнения системы. Перестановка уравнений должна быть предусмотрена в вычислительном алгоритме при его реализации на компьютере.<
и т.д. Поэтому они должны быть отличны от нуля. В противном случае необходимо соответственным образом переставить уравнения системы. Перестановка уравнений должна быть предусмотрена в вычислительном алгоритме при его реализации на компьютере.<
Обратный ход начинается с решения последнего уравнения системы (3.11):
 ,
,
затем из предпоследнего уравнения находится  :
:
 ,
,
аналогично определяются и все остальные неизвестные.
Ниже приведено описание вычислительного алгоритма метода Гаусса.
1. Ввод n,  ,
, 
2. Для i от 1 до  :
:
2.1. Если  , тогда Перестановка уравнений
, тогда Перестановка уравнений
2.2. Для k от  до n :
до n :
2.2.1. 
2.2.2. Для j от  до n :
до n : 
2.2.3. 
3. Для i от n до 1 с шагом –1 :
3.1. 
3.2. Для j от  до n :
до n : 
3.3. 
4. Вывод 
В приведенном алгоритме первый цикл с параметром i реализует прямой ход, а второй – обратный ход метода Гаусса.
Одной из модификаций метода Гаусса является схема с выбором главного элемента. Она состоит в том, что требование неравенства нулю диагональных элементов  , на которые происходит деление, заменяется более жестким: из всех оставшихся в i-м столбце элементов нужно выбрать наибольший по модулю и переставить уравнения так, чтобы этот элемент оказался на месте элемента
, на которые происходит деление, заменяется более жестким: из всех оставшихся в i-м столбце элементов нужно выбрать наибольший по модулю и переставить уравнения так, чтобы этот элемент оказался на месте элемента  . Это так называемый выбор главного элемента по столбцу. Существуют также схемы с выбором главного элемента по строке и по всей матрице.
. Это так называемый выбор главного элемента по столбцу. Существуют также схемы с выбором главного элемента по строке и по всей матрице.
Алгоритм выбора наибольшего элемента по столбцу достаточно прост и состоит из двух этапов: отыскание номера наибольшего элемента и перестановки элементов двух строк. Описание алгоритма приведено ниже.
1. 
2. Для m от  до n :
до n :
2.1. Если  , тогда
, тогда 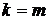
3. Если  , тогда
, тогда
3.1. Для j от i до n : 
3.2. 
Здесь k – номер наибольшего по абсолютной величине элемента матрицы в столбце с номером i. Этот алгоритм встраивается в приведенный выше алгоритм метода Гаусса вместо условной конструкции, выполняющей перестановку уравнений в случае равенства нулю элемента  (шаг 2.1.).
(шаг 2.1.).
Благодаря выбору наибольшего по модулю ведущего элемента уменьшаются множители, используемые для преобразования уравнений, а также снижается вероятность деления на малые числа, что в итоге способствует уменьшению вычислительных погрешностей.
Дата добавления: 2018-04-15; просмотров: 2173; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
