Определители (детерминанты) квадратных матриц

Глава 4. Численные методы алгебры.

Решение систем лИнейных уравнений

Линейные зависимости являются наиболее употребительными в математическом моделировании для построения как точных, так и приближенных зависимостей параметров моделей (ими являются неизвестные уравнений), поскольку они являются простейшим видом зависимости, для которого достаточно полно разработана теория и практические методы решения.

Методы решения систем линейных уравнений являются одной из основных частей численных методов алгебры - отдельного раздела вычислительной математики, посвященный численном методам решения задач линейной алгебры. Второй основной задачей является определение собственных значений и собственных векторов матрицы. Ряд других задач (обращение матриц, вычисление определителей, нахождение корней алгебраических многочленов) обычно носят вспомогательный характер при решении основных задач линейной алгебры.

Линейные уравнения. Теоретическое и практическое решения линейных уравнений с одним неизвестным

Линейными относительно неизвестных х₁, х₂,... х_n, называют степенное уравнения, содержащие неизвестные только в первое степени. Коэффициенты при неизвестных называют линейными, все остальные коэффициенты - свободными.

Пример 1 линейных уравнений:

1) ах + by = c; - линейное уравнение относительно неизвестных х,y, в котором а и b - линейные коэффициенты, c - свободный коэффициент;

2) 1,2х₁ + 4 + 5,08х₂- 13,17х₃- 4,38х₁ + 31,75х₂+ 1,3 = 3,8х₃ - 14,61; - линейное уравнение относительно неизвестных х₁,х₂,х₃, вещественными линейными и свободными коэффициентами.

Каноническим называют такой видлинейных уравнений, при котором все слагаемые, содержащие неизвестные (х₁, х₂,... х_n), находятся в левой части и выполнено приведение коэффициентов при неизвестных (а₁, а₂,... а_n), а приведенный свободный коэффициент (b) стоит в правой части уравнения:

а₁х₁+ а₂х₂+...+ а_nх_n = b. (4.1)

В примере 1 в каноническом виде представлено уравнение 1), уравнение 2) - нет.

Линейными уравнениями с одним неизвестным в каноническом виде называют зависимоститипа

а × х = b, (4.2)

где х- неизвестное, a, b - постоянные коэффициенты.

Теоретическим достаточным условием существования и единственности решения линейного уравнения (4.2) с одним неизвестным является условие

a ¹ 0. (4.3)

При его выполнении теоретическое решение (4.2) всегда существует, единственно и равно:

х = b / а. (4.4)

Теоретическое достаточное условие (4.3) выводится для идеального представления числовых коэффициентов уравнения и не учитывает реальный характер вычислений - как при ручном, так и при машинном расчетах. На практике из-за наличия погрешностей при задании исходных данных, а также погрешностей расчета практическое достаточное условие существования и единственности решения линейного уравнения (4.2) формулируют в виде:

ï a ï ³ e, (4.5)

где e > 0 - заранее задаваемое положительное число, задающее граничную величину предельной абсолютной погрешности коэффициента линейного коэффициента a, при которой он уже не считается равным или близким к нулю. Если условие (4.5) выполнено, то решение совпадает с (4.4).

Вопросы для проверки знаний.

1. Какой вид уравнений называют линейным ?

2. Какую форму имеют линейные уравнения канонического вида ?

3. В какой форме формулируются теоретическое и практическое условия существования решения линейного уравнения с одним неизвестным и чем вызвано их различие ?

Практические задания.

1.Привести к каноническому виду линейные уравнения:

a) х + y - 1 + 2x - 2y +3 = y + z + 10;

б) 0,2х₁ +2,8х₂+ 5,1х₃- 2,2 + 8,1х₃ + 1,8х₁+ 9,0 = 8,1х₁ - 7,5х₃ + 6,5;

в) уравнение 2) примера 1.

Системы линейных уравнений. Основные понятия

Системой m линейных уравнений с n неизвестными (или линейной системой) в линейной алгебре называют систему m линейных уравнений канонического вида с n неизвестными вида

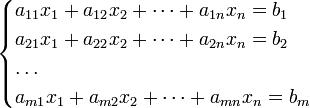
(4.6)

В (4.6) x₁, x₂, …, x_n — неизвестные, a₁₁, a₁₂, …, a_mn — постоянные линейные коэффициенты системы (задающие матрицу системы), b₁, b₂, … b_m — свободные члены (задающие вектор свободных коэффициентов). Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.

Систему (4.6) называются однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.

Система (4.6) называется квадратной, если число m уравнений равно числу n неизвестных. Число n= m называют порядком системы.

Решение системы (4.6) — совокупность n чисел c₁, c₂, …, c_n, таких что подстановка каждого c_i вместо x_i в систему (4.6) обращает все её уравнения в тождества. Найти решение системы означает выяснить, существует ли у системы решения, и если они существуют, найти их.

Система (4.6) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. Совместная система вида (4.6) может иметь одно или более решений.

Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной системы вида (4.6) называются различными, если нарушается хотя бы одно из равенств:

c₁⁽¹⁾ = c₁⁽²⁾, c₂⁽¹⁾ = c₂⁽²⁾, …, c_n⁽¹⁾ = c_n⁽²⁾.

Совместная система вида (4.6) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

В технических приложениях, как правило, рассматриваются системы с квадратными матрицами (m = n). Поэтому в дальнейшем будем рассматривать только этот случай.

Множество коэффициентов (a_ij) квадратной системы образуют ее матрицу А, а множество коэффициентов (b_i) – вектор `В свободных коэффициентов системы. Обозначив вектор (x₁, x₂, …, x_n) неизвестных через`Х, в векторном виде систему представляют в виде:

A`Х =`В. (4.7)

Вопросы для проверки знаний.

1. Какие системы линейных уравнений называют однородными, а какие – неоднородными ?

2. Какие системы линейных уравнений называют квадратными ?

3. Что называют решением системы линейных уравнений ?

4. Какие системы линейных уравнений называют определённой, неопределённой и переопределёнными ?

5. Как системы линейных уравнений представляют в векторной форме ?

Определители (детерминанты) квадратных матриц

Главной характеристикой квадратной матрицы является определитель (детерминант) - численная характеристика матрицы, которая может быть определена двумя способами - 1) либо рекурсивно по порядку матрицы n либо 2) при помощи перестановок. Обозначается определитель матрицы А как D(А) либо det(A).

Рекурсивное определение определителя матрицы А по ее порядку n.

n=1. Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:

(4.8а)

n³2. Для матриц второго порядка и выше детерминант задаётся рекурсивно формулой, которая называется разложением определителя по первой строке:

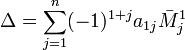, (4.8б)

где 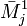— дополнительный минор к элементу a_1j. - определитель матрицы порядка (n-1), которая получается из А вычеркиванием в ней первой строки и столбца с номером j .

Определение определителяпри помощи перестановок. Для квадратной матрицы А порядка n справедлива формула:

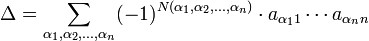, (4.9)

где α₁,α₂,...,α_n — перестановка чисел от 1 до n, N(α₁,α₂,...,α_n) — число инверсий (нарушений порядка) в перестановке, суммирование идёт по всем возможным перестановкам порядка n. Поскольку общее их число равно n!, то в сумму (4.9) войдут n! слагаемых, которые называют членами определителя.

Используя рекурсивное определение, найдем расчетные формулы для определителей матриц порядков n=2 и n=3.

(4.10)

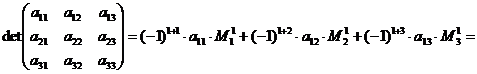
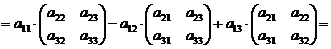
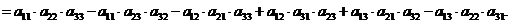(4.11)

Примеры 1. Расчет определителей:

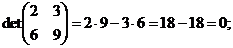
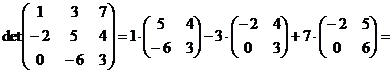
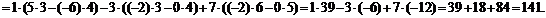
Свойства определителей

1. Определитель линеен по всем строкам (столбцам):

, где 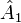и т. д. — строчки матрицы, 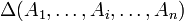— определитель такой матрицы.

2. При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.

3. Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.

4. Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.

5. Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).

6. Общий множитель элементов какого-либо ряда определителя (строки или столбца) можно вынести за знак определителя.

7. Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.

Расчет определителей

Непосредственный расчет определителя на основании его определения (как суммы по перестановкам, или с использованием рекурсивного разложения Лапласа по определителям меньшего порядка) затрачивает слишком много операций. Например, при использовании перестановок, не рассматривая генерации самих перестановок на формирование каждого слагаемого уходит (n-1) умножение. Поскольку всего таких перестановок n!, то общее число умножений равно (n-1)n!. Отсюда случает, что данный алгоритм имеет экспоненциальную сложность и для матриц высокого порядка не подходит.

Расчет определителя можно выполнять более эффективно, с использованием алгоритмов, имеющих полиномиальную сложность, которые будут рассмотрены далее.

Вопросы для проверки знаний.

1. Какие существуют два способа задания определителей ой вид уравнений называют линейным ?

2. Как формулируется рекурсивное задание определителя ?

3. Как формулируется задание определителя при помощи перестановок?

4. Всегда ли останется неизменным определитель квадратной матрицы, если:

а) к ее первой строке прибавить все остальные,

б) прибавить все коэффициенты первой строки к первому коэффициенту второй,

в) вычесть из первой строки вторую и третью,

г) циклически переставить местами первый, второй и третий столбцы (1®3,3®2,2®1) ?

Практические задания.

1. Рассчитать определители второго порядка:

а) 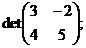б) в)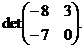

2. Рассчитать определители третьего порядка:

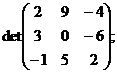а) б) в)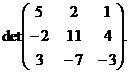

Дата добавления: 2018-04-15; просмотров: 323; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 Следующая ⇒

Мы поможем в написании ваших работ!