Недостатки (аберрации) оптических систем
При построении изображения малого предмета в тонкой линзе мы пользовались параксиальным пучком света. Кроме того, лучи параксиального пучка составляли небольшие углы с главной оптической осью. Далее, падающий свет считали монохроматическим, а показатель преломления материала линзы – не зависящим от длины волны падающего света. На практике всё эти условия не соблюдаются и возникают соответствующие недостатки оптических систем. Коротко остановимся на некоторых из них.
Сферическая аберрация. В случае тонкой линзы параксиальный пучок, исходящий из точки S, после преломления в линзе пересекает оптическую ось в одной точке. Если же пучок света, исходящий из источника S, составляет большой угол с главной оптической осью, то лучи, составляющие разные углы, пересекают оптическую ось не в одной точке, а в разных точках, например точки S1, S2, на рисунке 1.10.
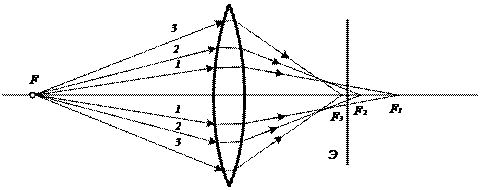
Рисунок 1.12 – Сферическая аберрация
Лучи, более удаленные от центра линзы, сильнее преломляются и пересекают главную оптическую ось на сравнительно близких расстояниях от центра линзы. Если экран Э, расположенный перпендикулярно главной оптической оси, передвигать влево от F1 к F2, то вместо стигматического точечного изображения получается расплывчатое пятно. Такая погрешность, связанная со сферичностью преломляющих поверхностей, называется сферической аберрацией.
Визуально сферическая аберрация проявляется в нечеткости (размытии) изображения по краям.
Для количественной характеристики сферической аберрации вводится понятие продольной аберрации. Линейная аберрация зависит от материала линзы, от кривизны поверхностей. Продольные аберрации собирательной и рассеивающей линз противоположны по знаку. Это позволяет, комбинируя такие линзы, уменьшить сферическую аберрацию.
Хроматическая аберрация. Из-за явления дисперсии (зависимость показателя преломления от длины волны) для данной линзы фокусы для разных цветов будут смещены друг относительно друга (на рисунке 1.13 показаны фокус Fф для фиолетовых и фокус Fkp для красных лучей). В результате этого изображения белого пятна или четкой границы свет-тень получаются цветными. Чередование цветов зависит от положения экрана, наблюдения, а соответствующее искажение носит название хроматической аберрации. Хроматическая аберрация, подобно сферической, количественно характеризуется продольной хроматической аберрацией (Fф, Fкp).
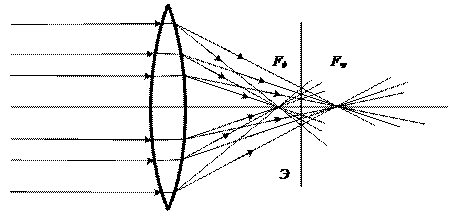
Рисунок 1.13 – Хроматическая аберрация
Для сведения по возможности к минимуму хроматической аберрации пользуются комбинацией линз, изготовленных из специально подобранных материалов. Такая система называется ахроматической. Ахроматические системы, безусловно, не могут полностью устранить хроматическую аберрацию. Самая простая ахроматическая система состоит из выпуклой линзы, изготовленной из кронгласа (легкого сорта стекла) и приклеенной к двояковыпуклой линзе из флинтгласа (тяжелого сорта стекла). Прибавление рассеивающей линзы к системе приводит к увеличению ее фокусного расстояния. Однако такое увеличение фокусного расстояния зависит от длины волны, причем фокусное расстояние для фиолетового света увеличивается больше, чем фокусное расстояние для красного света. Обычно при изготовлении ахроматической системы расчет производится так, чтобы фокусы для двух и более длин волн совпали.
Дисторсия изображения. В случае, когда лучи, участвующие в построении изображения, образуют достаточно большие углы с главной оптической осью, увеличение системы зависит от угла между пучком и главной оптической осью. В этом случае изображение не является подобным предмету. Это обусловлено тем, что отношение тангенсов углов поля зрения и поля изображения не является постоянной величиной для точек по всему полю изображения. Поэтому, например, предмет в виде правильного квадрата изображается в искаженном виде – в виде подушки, бочки или еще более сложной фигуры. Недостатки такого рода называются дисторсией. Соответствующий подбор составленных частей оптической системы позволяет сделать исправление на дисторсию. Оптическая система, свободная от дисторсии, называется ортоскопической.
Кома. Кривизна поверхности оптических систем кроме сферической аберрации вызывает также и другую погрешность – кому (рисунок 1.14). Лучи, идущие от точечного объекта, лежащего вне оптической оси системы, образуют в плоскости изображения в двух взаимно перпендикулярных направлениях сложное несимметричное пятно рассеяния, напоминающее по виду комету с хвостом. Поэтому подобная аберрация во внеосевых пучках была названа комой. На рисунке 1.14 представлено несимметричное пятно рассеяния в так называемой сагиттальной (перпендикулярной к оптической оси) плоскости. Кома обусловлена, как выше отметили, как сферичностью поверхности, так и удаленностью точки от оси, в результате чего построение изображения производится внеосевыми (наклонными) пучками. Действительно, при той же сферической поверхности в осевом пучке, вверх и вниз от оптической оси, существует полная симметрия в отношении преломления. В случае же наклонного пучка ввиду полного отсутствия подобной симметрии верхние и нижние части преломляются по-разному и в итоге получают различные погрешности.
Кома является одной из наиболее существенных аберраций. Поэтому, подбирая соответствующие совокупности частей оптической системы, нужно свести ее к минимуму. У системы с исправленной сферической аберрацией кома отсутствует, если для нее удовлетворено условие синусов Аббе. Если в оптической системе полностью устранены кома и сферическая аберрация для всего отверстия и всех наклонов лучей, то монохроматический свет в данной системе образует идеальное изображение, лишенное всех недостатков.

Рисунок 1.14 – Аберрация – кома
Астигматизм наклонных пучков. Астигматизм наклонных пучков (рисунок 1.15) заключается в том, что лучи одного и того же пучка, исходящие из точки и идущие в двух взаимно перпендикулярных плоскостях, после преломления в оптической системе, теряя гомоцентричность, не собираются в одну точку, а образуют две точки схода. Представим себе пучок лучей, исходящий из точки А и падающий на оптическую систему под углом к ее оси. Рассмотрим лучи, как бы выделенные крестообразной узкой диафрагмой, кресты которой направлены по меридиональной и сагиттальной плоскостям. Из такой диафрагмы выйдет плоская ленточка лучей, расположенных (при соответствующей ориентации крестов диафрагмы) в меридиональной и сагиттальной плоскостях. Эти ленточки лучей из-за различия кривизны по двум взаимно перпендикулярным направлениям преломляются по-разному, и в результате изображением точки А являются две линии на двух взаимно перпендикулярных фокальных плоскостях.
Линия ASAS образуется в результате преломления сагиттальных лучей и ориентирована в меридиональной плоскости, а линия Аm Аm образуется при преломлении меридиональных лучей и ориентирована в перпендикулярной плоскости. Эти две фокальные плоскости расположены на разных расстояниях от главной плоскости системы. Если изображение точки А в плоскости I служит линия Аm Аm , а в плоскости III – линия ASAS, перпендикулярная линии Аm Аm, то изображение при перемещении от плоскости I к плоскости III превращается в фигуры рассеяния в виде эллипсов различного эксцентриситета. Фигура рассеяния только в одной плоскости, расположенной посредине между плоскостями I и III, имеет вид круга (II). Следовательно, и в случае астигматизма наклонных пучков изображение точки имеет вид пятна рассеяния, форма которого, как следует из вышеизложенного, зависит от положения экрана наблюдения.


Рисунок 1.13 – Астигматизм наклонных лучей
Астигматизм оптической системы может быть исправлен путем подходящего подбора радиусов кривизны линз и их фокусных расстояний. Оптическая система, свободная от астигматизма, называется анастигматом.
Исправление всех недостатков оптической системы одновременно практически невозможно. В каждом конкретном приборе устраняется тот или иной недостаток, в зависимости от предназначения данного прибора.
Асферическая оптика. Возможности асферической оптики сравнительно со сферической оптикой видны при рассмотрении параметров, определяющих форму несферических поверхностей. Асимметричное сечение поверхности 2-го порядка выражается уравнением вида Y2 = Ax + Bx2, определяющим эллипс при В < 0 (окружность при В = -1), гиперболу при В > 0 и параболу при В = 0. Радиус кривизны кривой в её вершине равен r0 = А/2. Коэффициент В на этот радиус не влияет, и его изменения, влекущие изменения формы поверхности, не приведут к изменению ни фокусного расстояния, ни увеличения системы для параксиального пучка лучей, падающих на поверхность оптической детали такого сечения. Таким образом, несферические поверхности 2-го порядка, в отличие от сферы, характеризуемой только одним параметром – радиусом, имеют ещё один расчетный параметр, позволяющий изменять ход краевых лучей в системе, не затрагивая хода параксиальных лучей, что создаёт дополнительные возможности для построения оптических систем.
Ещё большие возможности открываются при использовании поверхностей более высоких порядков. Поэтому при расчёте оптических систем с заданными аберрациями одна асферическая поверхность может заменить
2 – 3 сферических, что приводит к резкому сокращению числа деталей системы. Асферическая оптика существенно расширяет возможности разработки оптических систем, но её распространение ограничивается сложностью изготовления и контроля асферических поверхностей. Хорошо отработанная технология изготовления сферических поверхностей, основанная на принципе притирания изготавливаемой поверхности и инструмента, неприменима в общем виде для асферических поверхностей из-за непостоянства их кривизны в разных местах детали. Асферическая оптика произвольной формы изготавливается с помощью инструмента, давление которого на обрабатываемую поверхность заданным образом зависит от расстояния до оси вращения детали.
Асферическая оптика без осевой симметрии (оптические системы с цилиндрическими линзами) имеет различные фокусные расстояния в разных плоскостях, проходящих через оптическую ось, т. е. обладает астигматизмом. Оптические системы с цилиндрическими линзами применяются в очках для исправления астигматизма глаза, в анаморфотных системах для получения различного масштаба изображения по разным направлениям.
Оптические приборы
Дата добавления: 2018-04-15; просмотров: 2308; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
