Призмы, плоскопараллельные пластины
ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ»
Кафедра «Физические методы контроля»
ПРИБОРЫ И МЕТОДЫ ВИЗУАЛЬНОГО И ОПТИЧЕСКОГО КОНТРОЛЯ
Методические указания к самостоятельной
Работе студентов специальности
Приборы и методы контроля качества и
Диагностики»
Часть 2
Могилев 2012
УДК 621.396.6
ББК 32.844
П 65
Рекомендовано к опубликованию
учебно-методическим управлением
ГУ ВПО «Белорусско-Российский университет»
Одобрено кафедрой «Физические методы контроля» 6.02.2012г
протокол № 4
Составители: канд. техн. наук, доц. В. Ф. Поздняков;
ст. преподаватель К. Б. Прудников,
ассистент Е. В. Позднякова
Рецензент д-р физ.-мат. Наук А.В. Хомченко
В методических указаниях кратко изложены основные теоретические сведения для самостоятельной работы студентов специальности 20 01 02 «Приборы и методы контроля качества и диагностики»
Учебное издание
ПРИБОРЫ И МЕТОДЫ ВИЗУАЛЬНОГО
И ОПТИЧЕСКОГО КОНТРОЛЯ
Часть 2
Ответственный за выпуск С. С. Сергеев
Технический редактор И.В. Русецкая
Компьютерная верстка И.П. Полевничая
|
|
|
Подписано в печать . Формат 60х84/16. Бумага офсетная. Гарнитура Таймс.
Печать трафаретная. Усл. -печ. л. . Уч. -изд. л. . Тираж 56 экз. Заказ №
Издатель и полиграфическое исполнение
Государственное учреждение высшего профессионального образования
«Белорусско-Российский университет»
ЛИ № 02330/0548519 от 16. 06.2009 г.
Пр. Мира, 43, 43212000, г. Могилев,
© ГУ ВПО «Белорусско-Российский
университет», 2012
Содержание
| 1 Геометрическая оптика.………..…………………………………... 1.1 Явление отражения и преломления света ………………………. 1.2 Призмы, плоскопараллельные пластины………………………… 1.3 Линзы.………….…………………………………………………… 1.4 Недостатки (аберрации) оптических систем……………………... 2 Оптические приборы ………………………………………………... 2.1 Классификация оптических приборов …………………………… 2.2 Общие характеристики оптических приборов…………………… 2.3 Лупы………………………………………………………………… 2.4 Телескопические системы ………………………………………… 2.5 Микроскопы………………………………………………………... 2.6 Типы микроскопов и методы оптической микроскопии………... 2.7 Эндоскопические приборы………………………………………... Список литературы………………………………………………… | 4 4 8 11 15 21 21 22 26 31 33 39 44 48 |
Геометрическая оптика
|
|
|
Явление отражения и преломления света
Поверхности любых объектов отражают свет. Интенсивность отражения зависит от состояния и свойства поверхности. Если бы поверхность не отражала свет, они казались бы нам абсолютно черными. Однако в ощущаемой природе нет таких объектов, которые бы полностью поглощали или отражали свет. Какая-то часть света всегда отражается от поверхности, а какая-то всегда поглощается.
Способность поверхности объекта отражать оптическое излучение характеризуется коэффициентом отражения
Котр = Iотр/Iпод,
где Iотр – сила отраженного света;
Iпод – сила падающего света.
Наблюдение солнечных и лунных затмений, геодезические измерения, образование теней и полутеней показали прямолинейность распространения света. Опыт показал, что закон прямолинейного распространения света несправедлив в случае прохождения лучей вблизи экранов. Здесь мы встречаемся с явлением дифракции. Однако геометрическая оптика не рассматривает явления дифракции.
|
|
|
Геометрическая оптика исходит из закона независимости распространения света. Сущность его заключается в том, что отдельные лучи и пучки света, встречаясь друг с другом, пересекаясь, не оказывают влияния друг на друга.
Другими основными законами, на которых базируется геометрическая оптика, являются законы отражения и преломления света.
Если лучи света, распространяясь в одной оптической среде, встречают другую среду, то на границе этих сред они полностью или частично отражаются (рисунок 1.1).

n1 – показатель преломления среды 1; n2 – показатель преломления среды 2
Рисунок 1.1 – Отражение света от плоской поверхности
При отражении лучи света подчиняются следующим законам:
а) падающий луч, отраженный луч и перпендикуляр, восстановленный к поверхности в точке падения, лежат в одной плоскости;
б) угол отражения равен углу падения (φ = φ1);
в) луч падающий и луч отраженный обратимы.
Если лучи света, встречая другую оптическую среду, преломляются (рисунок 1.2), то они подчиняются следующим законам:
а) луч падающий, луч преломленный и перпендикуляр, восстановленный к поверхности в точке падения, лежат в одной плоскости;
|
|
|
б) отношение синуса угла падения луча к синусу угла преломления луча для двух данных оптических сред есть величина постоянная и называется она относительным показателем преломления двух сред (формула 1.1);
в) луч падающий и луч преломленный обратимы.

n1 – показатель преломления среды 1; n2 – показатель преломления среды 2
Рисунок 1.2 – Преломление света на границе двух сред
Относительный показатель преломления двух сред
 , (1.1)
, (1.1)
где φ – угол падения;
ψ – угол преломления;
v1 – скорость света в среде 1;
v2 – скорость света в среде 2.
Таким образом, относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления.
Исходя из вышеизложенного, закон преломления можно представить в виде
n1· sin φ = n2· sin ψ.
Из этой формулы видно, что при переходе света из оптически боле плотно среды в менее плотную, угол преломления больше чем угол падения.
Результат преломления света представлен на рисунке 1.3. Ложка, опущенная в стакан, с водой кажется согнутой.

Рисунок 1.3 – Результат преломления света
Некоторые показатели преломления оптически прозрачных веществ приведены ниже: алмаз 2,42, кварц 1,54, воздух (при нормальных условиях) 1,00029, этиловый спирт 1,36, вода 1,33, лёд 1,31, плавленый кварц 1,46, крон 1,52, лёгкий флинт 1,58, хлорид натрия (соль) 1,53.
Показатель преломления n несколько меняется в зависимости от длины волны света – постоянное значение он сохраняет только в вакууме. Поэтому приведённые выше данные соответствуют желтому свету с длинной волны λ = 589 нм.
Увеличение угла падения φ сопровождается более быстрым ростом угла преломления ψ, и при достижении углом φ значения
φ пред = arcsin n12 (1.2)
угол ψ становится равным 90о. Угол, определяемый формулой 1.2, называется предельным углом (рисунок 1.4).
а) б)
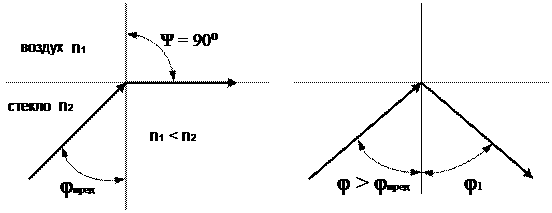
а – предельное значение угла преломления; б – полное внутреннее отражение при φ > φпред
Рисунок 1.4 – К понятию явления полного внутреннего отражения
Энергия, которую несет с собой падающий луч, распространяется между отраженным и преломленным лучами. По мере увеличения угла падения интенсивность отраженного луча растет, интенсивность же преломленного луча падает, обращаясь в нуль при предельном угле (рисунок 1.4). При углах падения, заключенных в пределах от φ пред до π/2, световая волна проникает во вторую среду на расстоянии порядка длины волны λ и затем возвращается в первую среду. Это явление называется явлением полного внутреннего отражения.


1– преломленные лучи света; 2 – луч света, претерпевший полное внутреннее отражение
Рисунок 1.5 – Явление преломления и полного внутреннего отражения
Предельный угол падения для стекла составляет приблизительно 42º, для воды 47,5º.
На рисунке 1.5 проиллюстрированы явления преломления и полного внутреннего отражения.

Призмы, плоскопараллельные пластины
Явление полного внутреннего отражения широко используется в оптических элементах, таких как призмы, волоконной оптике.
Оптические призмы являются одним из основных элементов при создании оптических систем и оптических приборов. Призмы широко используются в оптических приборах различного назначения, таких как наблюдательные оптические приборы (телескопы, бинокли, микроскопы и другие), оптические приборы для регистрации изображений на электронных приёмниках, сложные многофункциональные оптические приборы. Причём, чем сложнее оптический прибор, тем большее количество и номенклатура оптических призм может в нём использоваться. Например, большое число сложных оптических призм используется в таких оптических приборах как спектральные оптические приборы, интерферометры, поляриметры и другие.
Оптические призмы в зависимости от их оптической конструкции функционально позволяют:
– изменять ход лучей в оптических приборах;
– изменять направление оптической оси системы;
– изменять направление линии оптического визирования;
– оборачивать оптические изображения;
– использовать их в качестве отражателей;
– уменьшать габариты оптических систем;
– разделять пучки лучей в оптических системах;
– объединять поля в оптических системах;
– вращать в оптических системах изображения;
– компенсировать в оптических системах поворот изображения;
– разлагать белый свет в спектр;
– получать поляризованный свет.
Следует отметить, что действие оптической призмы подобно зеркалу, однако в ряде случаев использовать оптические призмы удобнее, чем зеркала. Отметим некоторые преимущества призм перед зеркалами:
– действие одной призмы часто заменяет действие системы зеркал: углы между зеркалами должны регулироваться с большой точностью при сборке, система зеркал подвержена разъюстированию, углы между гранями призмы неизменны;
– потери света у призм от граней с полным внутренним отражением равны нулю, тогда как при отражении от поверхностей зеркал потери довольно велики; кроме того, отражающие покрытия зеркал с течением времени могут портиться;
– конструкция крепления призм в оправах, как правило, проще чем системы зеркал, имеет меньшие габариты;
– для некоторых призм нет эквивалентных зеркальных систем (например, призма Дове, полупента, некоторые виды спектральных призм).
Внешний вид некоторых типов призм приведен на рисунке 1.5.
|
|

|
|
|
|









1 – пентапризма; 2 – прямоугольные призмы; 3 – пентапризма с крышей; 4 - плоскопараллельные пластины; 5 – призма Дове; 6 – триппель-призмы (уголковые отражатели)
Рисунок 1.6 – Оптические призмы
Прямоугольные призмы служат для изменения направления лучей света и для отражения (рисунок 1.7) .
Оборачивающие призмы служат для поворота изображения на 180º. Дело в том, что практически любая оптическая система (бинокль, подзорная труба, микроскоп), имеющая объектив и окуляр передает изображение повернутое слева на право и сверху вниз. Для оборачивания изображения в «нормальное» для нас положение в данных приборах служат соответствующие призмы (рисунок 1.7, в) или призменные системы.
Во многих оптических приборах различных конструкций применяются однотипные оптические детали в виде плоскопараллельных пластин. Они используются для защитных целей, для предметных стекол, компенсационных стекол, светофильтров, сеток зеркал.

А – поворачивающая прямоугольная призма; б – отражающая прямоугольная призма;
в – оборачивающая призма (призма Дове)
Рисунок 1.7 – Ход лучей в призмах
Ход лучей света через плоскопараллельную платину показан на рисунке 1.8.

Рисунок 1.8 – Ход лучей в плоскопараллельной пластине
Луч света, проходя через такую пластину выходит из нее под таким же углом под каким он попал на поверхность (параллельно), то есть φ = φ'. При этом он смещается на величину b, которая зависит от толщины пластины S и разности показателей преломления n1 и n2.
Уравнение смещения нулевого луча плоскопараллельной пластики вдоль оптической оси имеет следующий вид
L0 =  . (1.3)
. (1.3)
Представляет интерес величина поперечного смещения b луча, вышедшего из пластины по отношению к падающему
b =  . (1.4)
. (1.4)
Данные смещения в отдельных случаях приводит к аберрации и астигматизму, что необходимо учитывать при расчете оптических систем.
Линзы
Для концентрации оптического излучения, формирования изображения, согласования оптических систем служат широко распространенные оптические элементы – линзы.
Линзы – это прозрачные для света тела, ограниченные хотя бы с одной стороны сферической или иной поверхностью вращения.
Линзы могут быть положительные (выпуклые, фокусирующие, собирающие) и отрицательные (вогнутые, рассеивающие). По форме образующих их поверхностей существует шесть типов линз: три положительные и три отрицательные (рисунок 1.9).
Линзы, имеющие одну поверхность плоской (план-форма), это плосковыпуклые и плосковогнутые линзы (рисунок 1.9, а, 1.9, г).
Линзы, имеющие различные знаки радиусов кривизны поверхности (би-форма), это двояковыпуклые и двояковогнутые линзы (рисунок 1.9, б, 1.9, д).
Линзы имеющие одинаковые знаки радиусов кривизны, это выпукло-вогнутые и вогнуто-выпуклые линзы (рисунок 1.9, в, 1.9, е). Они называются менисками.
Основными характеристиками линз являются: фокусное расстояние и световой диаметр (рисунок 1.10).
Если на положительную линзу направить параллельные лучи света, то они соберутся в некоторой точке F называемой фокусом, а расстояние от фокуса до некоторой плоскости линзы называется фокусным расстоянием f. Фокусное расстояние является основной геометрической характеристикой линзы. Оно не зависит от диаметра линзы, а зависит только от радиуса кривизны сферической поверхности образующей линзу.

а – плоско-выпуклая; б – двояковыпуклая; в – выпукло-вогнутая; г – плоско-вогнутая; д – двояковогнутая; е – вогнуто-выпуклая
Рисунок 1.9 – Типы линз
Световой диаметр, это диаметр линзы, через который проходит световой поток. Так как часть линзы не участвует в формировании светового потока, а служит для закрепления в оправке оптического прибора, то диаметр самой линзы d не равен световому диаметру dсв.
Световой диаметр является энергетической характеристикой линзы, поскольку чем больше диаметр, тем больше светового потока может собрать линза. Световой диаметр определяет светосилу объективов оптических приборов. Чем больше оптический диаметр, тем больше светосила.
Величина, обратная фокусному расстоянию, называется оптической силой линзы
D = 1/f. (1.5)
а)

б)

а – положительная линза; б – отрицательная линза
Рисунок 1.10 – Основные характеристики линз
За единицу оптической силы линзы принимается такая линза, фокусное расстояние которой один метр и называется она диоптрией.
Оптическая система линзы (рисунок 1.11) представлена в виде системы главных поверхностей Н и Н'. Предмет l, расположенный в точке А находится на расстоянии х от точки переднего фокуса. Изображение l' графически определяется пересечением в пространстве двух лучей, один из которых выходит из точки В и идет параллельно оптической оси, а другой направляется в точку переднего фокуса. По выходе из системы первый луч должен пройти через точку заднего фокуса F', а другой – параллельно оптической оси. Оба луча пересекаясь в точке В' и образуют изображение l' .

Рисунок 1.11 – К выводу формулы Ньютона
Из подобия треугольников BAF и FHN следует
 . (1.6)
. (1.6)
Аналогично из подобия треугольников N´H´F´ и F´A´B´
 . (1.7)
. (1.7)
Отсюда получаем выражение, называемой формулой Ньютона
 . (1.8)
. (1.8)
При условии, что n = n´, формула Ньютона имеет вид
 . (1.9)
. (1.9)
Из выражений (1.6), (1.7) получаем формулы линейного увеличения идеальной оптической системы
β = -f/х; β = -х'/f'. (1.10)
Согласно рисунка 1.11, имеем х = а – f и х' = а' – f'. Подставляя эти выражения в формулу (1.8) и раскрывая скобки, получим
 . (1.11)
. (1.11)
Если система находится в однородной среде, то выражение (1.11) принимает вид формулы, известной под названием формулы отрезков
 . (1.12)
. (1.12)
Соотношения (1.8) – (1.12) представляют собой формулы центрированной оптической системы.
Дата добавления: 2018-04-15; просмотров: 1625; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
