Тема 3. Произведение векторов
10. Скалярное произведение векторов
К линейным операциям над векторами относятся сложение векторов и умножение вектора на число. Скалярное произведение не относится к линейным операциям.
Определение. Скалярным произведением двух векторов 
и 
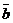называется число, равное произведению длин этих векторов на косинус угла между ними:
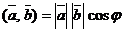. (1)
«Скаляр» (лат.) – число.
Скалярное произведение обозначают еще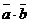 
.
Свойства скалярного произведения:
1) 
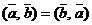– коммутативность;
2) 
;
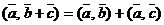3) 
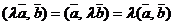; свойства линейности.
4) 
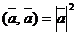, откуда 
;
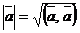5) 
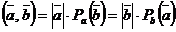, следовательно, 
;
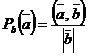6) Пусть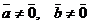 
. Вектор перпендикулярен вектору 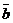тогда и только тогда, когда 
.
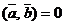Свойства 1, 3 – 5 следуют из определения.
Докажем свойство 6.
I.Необходимость.
Допустим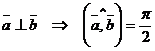 
. Тогда 
.
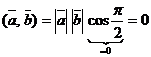II.Достаточность.
Пусть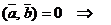 
.
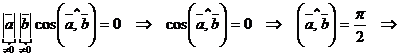
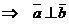Из формулы (1), которая определяет скалярное произведение можно найти угол между векторами. Пусть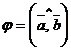 
. Тогда
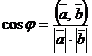. (2)
Далее находим 
через 
.
Получим формулы скалярного произведения в координатной форме. Допустим, что заданы два вектора
.
Это означает, что в системе координат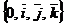 
они имеют разложения:
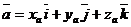, (3)
|
|
|
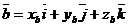. (4)
Перемножим равенства (3) и (4) скалярно, пользуясь свойствами 1) – 4) скалярного произведения. Получим
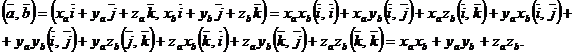
Получили формулу вычисления скалярного произведения векторов в координатной форме
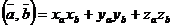. (5)
Используя формулу (5) запишем формулу (2) в координатной форме
.
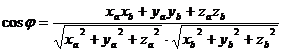20. Векторное произведение
В результате векторного произведения получаем вектор.
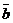Определение 1. Векторным произведением векторов и называется вектор, обозначаемый 
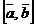или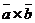 
и удовлетворяющий следующим трем условиям:
1) 
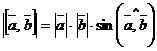; (1)
2) 
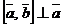и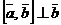 
;
3) векторы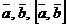 
образуют правую тройку векторов
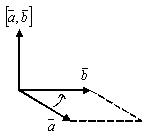
Правая часть равенства (1) геометрически задает площадь параллелограмма, построенного на векторах , 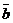. Значит модуль векторного произведения равен площади параллелограмма, построенного на векторах , .
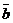Свойства векторного произведения:
1) 
;
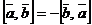2) 
;
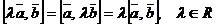3) 
;
;
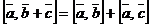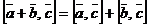4) два ненулевых вектора , 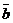коллинеарны тогда и только тогда, когда
|
|
|
.
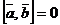Доказательство следует из определения 1.
Допустим векторы , 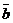заданы в координатной форме:
.
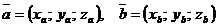Можно доказать формулу вычисления векторного произведения в координатной форме:
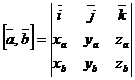. (2)
В правой части равенства (2) – определитель. Раскладывая его по первой строке, получим координаты вектора, равного векторному произведению.
30. Смешанное произведение векторов
В результате находжения смешанного произведения получаем число.
Определение. Смешанным произведением векторов , , 
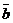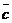называется скалярное произведение вектора 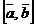и вектора :
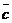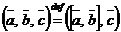. (1)
Фактически смешанное произведение – результат двух операций: векторного произведения и скалярного произведения.
Геометрические свойства смешанного произведения:
1) 
,
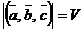где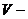 
объем параллелепипеда, построенного на векторах , , ;
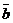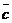2) векторы , , 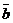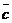образуют правую тройку вектором тогда и только тогда, когда 
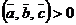; левую – когда 
;
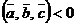3) Условие компланарности векторов. векторы , , 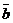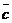компланарны тогда и только тогда, когда их смешанное произведение равно нулю, т.е. 
.
|
|
|
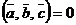Алгебраические свойства смешанного произведения:
1) 
;
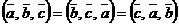2) 
;
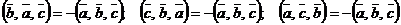3) 
;
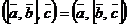4) 
;
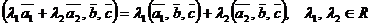5) 
.
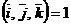Пусть векторы , , 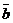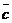заданы своими координатами
.
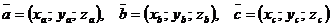Тогда смешанное произведение в координатной форме вычисляется с помощью определителя:
.
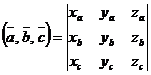Тогда условие компланарности векторов , , 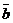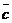можно переписать в виде
.
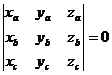Дата добавления: 2018-04-15; просмотров: 216; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!