Алгебраическая проекция – число.
РАЗДЕЛ 2: ВЕКТОРНАЯ АЛГЕБРА
Тема 1. Векторы в пространстве
10. Понятие вектора
Скалярная величина (скаляр) определяется только числом, которое показывает сколько определенных единиц измерения характеризуют эту величину (длина, площадь, объем, масса, температура и др.). Величины, которые характеризуются не только числом, но и направлением – векторные (скорость, сила и др.)
Направленным отрезком называется отрезок определенной длины и определенного направления.
Вектор – направленный отрезок.
Вектором также называют упорядоченную пару точек.
Если конец и начало отрезка фиксированы, то вектор – связанный. Связанные вектора обозначают  , если А – начало, В – конец.
, если А – начало, В – конец.
Если для вектора определяют лишь направление и длину (без фиксированных начала и конца), то данные векторы называют свободными. Как правило их обозначают  . Свободный вектор может перемещаться в пространстве без изменения своего направления и параллельно самому себе.
. Свободный вектор может перемещаться в пространстве без изменения своего направления и параллельно самому себе.
Модулем вектора 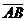 (или
(или  ) называется длина отрезка, которая ему соответствует. Модуль – длина вектора. Обозначается
) называется длина отрезка, которая ему соответствует. Модуль – длина вектора. Обозначается 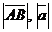 .
.
Вектор, длина которого равна единицы называется единичным вектором или ортом. Как правило единичный вектор обозначают  .
.
Вектор, длина которого равна рулю – нулевой вектор. Обозначается 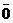 .
.
Всякий ненулевой вектор можно унормировать, т.е. создать для него единичный вектор
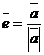 .
.
Два вектора коллинеарны (параллельны), если они лежат на одной или на параллельных прямых. Обозначают 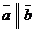 . Среди коллинеарных векторов различают сонаправленные (обозначают
. Среди коллинеарных векторов различают сонаправленные (обозначают 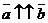 ) и противоположнонаправленными (обозначают
) и противоположнонаправленными (обозначают  ).
).
|
|
|
Два вектора называют равными, если один из них может быть получен из другого путем параллельного переноса.
Если рассматривать связанные векторы, то равенство двух векторов определяют как совпадение их начал и концов. Если рассматривать свободные векторы, то  , если
, если 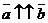 и
и 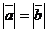 .
.
Исходя из смысла векторов можно утверждать, что для всякого свободного вектора  можно построить единственный связанный вектор
можно построить единственный связанный вектор 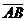 с началом в точке А, такой, что
с началом в точке А, такой, что 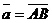 .
.
Последнюю запись понимают: свободный вектор перенесен в точку А.
Векторы 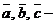 компланарные, если они лежат в одной плоскости или параллельны одной и той же плоскости.
компланарные, если они лежат в одной плоскости или параллельны одной и той же плоскости.
Углом между векторами  и
и  называется наименьший угол, на который нужно повернуть один вектор, чтобы его направление совпало с направлением другого вектора. Обозначают
называется наименьший угол, на который нужно повернуть один вектор, чтобы его направление совпало с направлением другого вектора. Обозначают 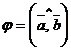 .
.
Для нахождения угла между векторами (геометрически) их начала совмещают. Исчисляется в пределах  .
.
Если 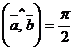 , то векторы ортогональны (перпендикулярны),
, то векторы ортогональны (перпендикулярны), 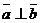 .
.
20. Линейные операции над векторами
К линейным операциям относятся умножение вектора на число и сложение (вычитание) векторов.
|
|
|
Сложение векторов
Чтобы сложить два вектора в пространстве (на плоскости) можно использовать геометрический метод треугольника или параллелограмма.
Допустим в пространстве заданы три вектора  . Их сложение можно произвести по правилу параллелепипеда или ломанной.
. Их сложение можно произвести по правилу параллелепипеда или ломанной.
При сложении векторов методом параллелепипеда их начала совмещают. Вектор-диагональ – сумма векторов, начало которого совпадает с началом векторов  :
:

Сумму конечного количества векторов находят по правилу ломанной, которая необязательно лежит в одной плоскости. Вектор-сумма – вектор, соединяющий начало первого вектора с концом последнего.
Для операции сложения векторов справедливы свойства:
1) для всяких векторов  существует единственный вектор
существует единственный вектор 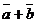 ;
;
2) 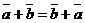 – коммутативность сложения;
– коммутативность сложения;
3) 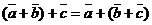 – ассоциативность;
– ассоциативность;
4)  .
.
Умножение вектора на число
Определение. Вектором 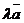 , где
, где 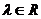 называется такой вектор, что
называется такой вектор, что
1) 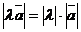 ;
;
2) 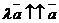 , если
, если 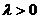 ;
;
3) 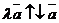 если
если 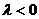 ;
;
4)  .
.
Вектор 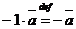 называется противоположным для вектора
называется противоположным для вектора  ;
;  +
+  .
.
Свойства операции умножения вектора на число:
1) для всякого вектора  и всякого числа
и всякого числа 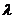 существует единственный вектор
существует единственный вектор 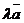 ;
;
|
|
|
2) 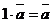 ;
;
3) 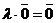 ;
;
4)  – ассоциативность;
– ассоциативность;
5) 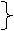
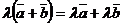 ;
;
6) 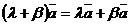 . дистрибутивность
. дистрибутивность
В этих свойствах  произвольные действительные числа;
произвольные действительные числа;  произвольные векторы.
произвольные векторы.
3. Разность векторов определяется равенством

следует из 1. и 2.
30. Проекция вектора
Прямую 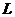 называют осью, если на ней задано направление.
называют осью, если на ней задано направление.
Углом между вектором и осью называют наименьший угол, на который надо повернуть вектор, чтобы его направление совпало с направлением оси.
Рассмотрим определенный вектор  и ось
и ось 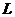

Рис.1 Рис.2 Рис.3
Спроектируем перпендикулярно начало и конец вектора  на ось
на ось 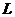 . Полученные точки будем считать соответственно началом и концом вектора
. Полученные точки будем считать соответственно началом и концом вектора 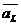 , который называется геометрической проекцией вектора
, который называется геометрической проекцией вектора  на ось
на ось 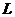 (рис. 1 – 3).
(рис. 1 – 3).
Вектор геометрической проекции может иметь направление, совпадающее с направлением оси 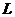 или противоположное этому направлению. Он также может быть точкой (рис.2), т.е. нулевым вектором
или противоположное этому направлению. Он также может быть точкой (рис.2), т.е. нулевым вектором 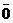 .
.
Введем на оси 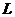 определенный масштаб.
определенный масштаб.
Определение. Алгебраической проекцией вектора  на ось
на ось 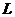 называется длина его геометрической проекции, взятая со знаком «+», если ее направление совпадает с направлением оси
называется длина его геометрической проекции, взятая со знаком «+», если ее направление совпадает с направлением оси 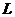 и со знаком «–», если направление противоположно.
и со знаком «–», если направление противоположно.
|
|
|
Алгебраическая проекция обозначается 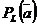 .
.
На рис. 1-3 соответственно имеем:
 ;
;
 ;
;
 .
.
Всюду далее будем рассматривать только алгебраическую проекцию, которую будем называть проекция.
Алгебраическая проекция – число.
Для проекции справедлива формула:
 , (1)
, (1)
где  .
.
40. Линейная зависимость и независимость векторов
Рассмотрим векторы
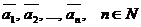 (1)
(1)
Определение 1. Линейной комбинациейвекторов (1) называется выражение вида
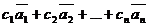 (2)
(2)
где 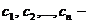 произвольные действительные числа.
произвольные действительные числа.
В результате нахождения линейной комбинации любых векторов получаем вектор.
Определение 2. Векторы (1) – линейно независимы, если равенство
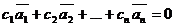 (3)
(3)
выполняется только в случае 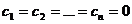 .
.
Определение 3. Векторы (1) линейно зависимы, если существует хотя бы одно ненулевое число  такое, что выполняется равенство (3).
такое, что выполняется равенство (3).
Теорема 1. Векторы (1) линейно зависимы тогда и только тогда, когда хотя бы один из них является линейной комбинацией остальных.
Доказательство:
I. Необходимость.
Допускаем, что векторы (1) линейно зависимы, т.е. равенство (3) выполняется при некотором ненулевом коэффициенте, например  . Тогда из (3)
. Тогда из (3)
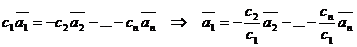 .
.
II. Достаточность.
Допустим, некоторый вектор является линейной комбинацией остальных векторов
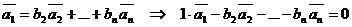 .
.
Получили равенство типа (3), причем есть хотя бы один ненулевой коэффициент при 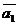 .
.
Т.е. векторы линейно зависимы.
Следствие 1. Для того, чтобы два вектора были линейно зависимы, необходимо и достаточно, чтобы они были коллинеарны.
Доказательство:
I. Необходимость.
Если векторы 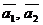 коллинеарны, то существует число
коллинеарны, то существует число 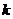 такое, что
такое, что
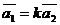 .
.
По теореме 1 векторы линейно зависимы.
II. Достаточность.
Пусть векторы 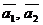 линейно зависимы, тогда существуют числа
линейно зависимы, тогда существуют числа  , среди которых есть ненулевое, что выполняется условие линейной зависимости
, среди которых есть ненулевое, что выполняется условие линейной зависимости
 .
.
Допустим  . Тогда
. Тогда 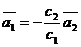 .
.
Это и есть условие коллинеарности.
Следствие 2. Для того, чтобы три вектора в пространстве были линейно зависимы необходимо и достаточно, что они были компланарными.
Следствие 3. Всякие три вектора на плоскости являются линейно зависимыми.
Следствие 4. Всякие четыре вектора в пространстве являются линейно зависимыми.
50 Базис
В физике встречаются задачи, когда действия двух сил 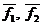 заменяется результирующие силой (суммой векторов). Встречается и обратная задача, когда действие силы
заменяется результирующие силой (суммой векторов). Встречается и обратная задача, когда действие силы 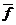 нужно выразить через
нужно выразить через 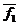 и
и 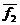 . Понятие разложения вектора по другим векторам широко используется в математике.
. Понятие разложения вектора по другим векторам широко используется в математике.
Определение 1. Вектор  называется разложенным по векторам
называется разложенным по векторам 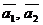 , если он представлен в виде линейной комбинации
, если он представлен в виде линейной комбинации
 ,
,  (1)
(1)
В пункте 40 (следствие 3) отмечено, что всякие три вектора плоскости являются линейно зависимыми.
Теорема 1. Всякий вектор плоскости можно единственным образом разложить по двум неколлинеарным векторам.
Доказательство.
|
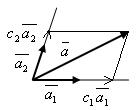
Из определения суммы векторов по правилу параллелограмма получаем
 (2)
(2)
Согласно (1) это означает, что вектор  разложен по векторам
разложен по векторам 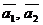 .
.
Докажем единственность такого разложения.
Допустим, что существует еще одно разложение, где 
 (3)
(3)
Вычтем (3) из (2)
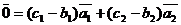 (4)
(4)
При рассмотрении общего случая  из (4) получаем
из (4) получаем
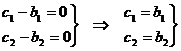 (5)
(5)
Пришли к противоречию, т.е. разложение единственное. При этом учитывали, что по условию 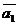 не ||
не || 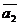 , т.е. равенство (4) может выполнятся только при условии (5).
, т.е. равенство (4) может выполнятся только при условии (5).
Теорема 2. Всякий вектор пространства можно единственным образом разложить по трем некомпланарным векторам.
Доказательство аналогичное доказательству теоремы 1. Совмещаем начало всех четырех векторов и заданный вектор проектируем на направления векторов 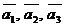 . Далее рассматриваем вектор
. Далее рассматриваем вектор  как сумму полученных геометрических проекций по правилу параллелепипеда (т.е.
как сумму полученных геометрических проекций по правилу параллелепипеда (т.е. 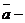 диагональ параллелепипеда ). Доказываем единственность.
диагональ параллелепипеда ). Доказываем единственность.
Определение 2. Базисом на плоскости называется всякая упорядоченная пара неколлинеарных векторов.
Определение 3. Базисом в пространстве называется всякая упорядоченная тройка некомпланарных векторов.
Общим для понятия базиса на плоскости и в пространстве является линейная независимость векторов. Их упорядоченность означает, что определенный вектор считается первым, некоторый – вторым и третьим. Теорема 1 означает, что всякий вектор на плоскости можно единственным образом разложить по базису. Теорема 2 означает, что всякий вектор в пространстве можно единственным образом разложить по базису.
Рассмотрим базис 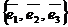 в пространстве (векторы необязательно единичные, каждый из них как бы задает единицу длины в своем направлении).
в пространстве (векторы необязательно единичные, каждый из них как бы задает единицу длины в своем направлении).
Определение 4. Координатами вектора  в базисе
в базисе 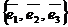 называют числовые коэффициенты в разложении вектора по базису
называют числовые коэффициенты в разложении вектора по базису
 (6)
(6)
Координаты вектора записывают
 (7)
(7)
т.е. как упорядоченную тройку чисел. Аналогично вводятся координаты вектора на плоскости как упорядоченная пара чисел.
Допустим, что вектор  задан в виде (6), т.е. имеет координаты (7) и задан вектор
задан в виде (6), т.е. имеет координаты (7) и задан вектор 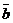
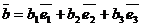 (8)
(8)
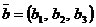
Рассмотрим сумму 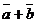 . Для этого сложим равенства (6) и (8). Приведя подобные получим
. Для этого сложим равенства (6) и (8). Приведя подобные получим
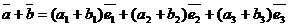 (9)
(9)
Из (9) следует, что координаты вектора-суммы равны сумме координат векторов-слагаемых
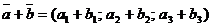 .
.
Аналогично можно доказать, что при умножении вектора на число каждая его координата умножается на это число, а также, что равные векторы имеют равные координаты, т.е.
 ;
;

Дата добавления: 2018-04-15; просмотров: 1116; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

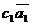 ,
, 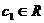 , во втором -
, во втором - 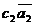 ,
, 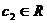 .
.