Эквивалентность различных форм задач линейного программирования
Две формы записи задачи линейного программирования эквивалентны, если любому допустимому решению одной из них соответствует единственное допустимое решение другой и при этом целевые функции обеих задач равны.
Две формы записи задачи линейного программирования эквивалентны, если оптимальному решению одной задачи соответствует оптимальное решение другой задачи и при этих оптимальных решениях значения целевых функций равны.
ПустьХи(х 10, х 20 ,…, х n0); Хк(х 10, х 20 ,..., х n0, х n+10). Хи ~ Х к - эквивалентные допустимые решения исходной и канонической форм. При этом Z(Хи) = Z(Хк).
ПустьХи(х 1*, х 2* ,…, х n*); Хк(х 1*, х 2* ,..., х n*, х n+1*). Хи*~ Х к* -
эквивалентные оптимальные решения исходной и канонической форм задачи линейного программирования. Тогда Z(Хи*) = Z(Хк*). Z(Хи*) ³ Z(Хи). Z(Хк*) ³ Z(Хк) (при решении на максимум Z).
Если две задачи линейного программирования эквивалентны, то достаточно найти оптимальное или хотя бы допустимое решение только в одной форме записи задачи. Решение в другой форме можно записать без повторного решения задачи в этой форме, а пользуясь лишь правилами соответствия.
Правило перехода от одной формы к другой обеспечивает эквивалентность задач.
Задача линейного программирования, записанная в исходной форме, эквивалентна как задаче, записанной в канонической форме, так и задаче, записанной в однородной форме.
Общая постановка задачи
|
|
|
Дана задача в канонической форме:
max Z = C1*x1 + C2*x2 +...+ Cn*x n+ C0
a 11 x 1 + a 12 x 2 +...+ a 1n. x n = a 10
a 21 x 1 + a 22 x2 +...+ a 2n x n = a 20
......................................................................
a m 1 x 1 + a m 2 x2 +...+ a m n x n= a m 0
x j ≥ 0 , j = 1¸ n.
С помощью преобразований Жордана - Гаусса получить каноническую форму с единичным базисом (случай 1), а затем получить задачу в однородной форме:
max Z = C`1 *x1 + C`2*x2 +...+ C`k*x k+ C`0
a` 11 x 1 + a` 12 x 2 +...+ a` 1k. x k ≤ a` 10
a` 21 x 1 + a` 22 x2 +...+ a` 2k x k ≤ a` 20
......................................................................
a`m 1 x 1 + a` m 2 x2 +...+ a` mk x k≤ a` m 0
x j ≥ 0 , j = 1¸ k.
Пример выполнения работы
Перейти от канонической формы к однородной форме.
max Z = x1 + x2 + x3+ x4
 (А)
(А)
1. В задаче два ограничения. Следовательно, m = 2. Выпишем все возможные группы из четырех переменных по две.
x1 x2; x1 x3; x1 x4; x2 x3; x2 x4; x3 x4
Найдем определители из коэффициентов при переменных этих групп:
x1 x2

x1 x3

x1 x4

x2 x3

x2 x4
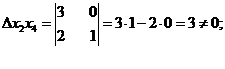
x3 x4

Для всех групп переменных определители отличны от нуля. Следовательно, данную систему можно привести к шести сочетаниям базисных переменных.
Перейдем к сочетанию базисных переменных х1 х2.
2. Перенесем в левую часть все элементы целевой функции. Получим
|
|
|
Z - x1 - x2 - x3 - х4 = 0.
3. Запишем систему ограничений и измененную целевую функцию в таблицу Гаусса. Получим таблицу 2.
Столбец контрольной суммы - это сумма всех элементов строки.
Таблица 2
| Базисные переменные | Переменные | ||||||||||
| Z | x1 | x2 | x3 | x4 | aio | kΣ | |||||
| - | 0 | 1 | 3 | 1 | 0 | 5 | 10 | ||||
| - | 0 | 3 | 2 | 2 | 1 | 10 | 18 | I* | |||
| Z | 1 | -1 | -1
 Мы поможем в написании ваших работ! | ||||||||
