Соответствие решений канонической, исходной и однородной форм задач линейного программирования
Допустимому решению задач в исходной форме Хи 0(х10 , х20 ,...,хn0 ) соответствует решение задачи в канонической форме:
Х к 0(х10 , х20 ,...,хn0 , хn+10 ,…, хn+m-l0),
где n - число основных переменных, m - число ограничений, l - число ограничений равенств. Дополнительные переменные хn+10 , …, хn+m-l0 вычисляются как разность между правой и левой частью соответствующего неравенства типа меньше либо равно.
Допустимому решению в канонической форме:
Х к 0(х10 , х20 ,...,хn0 , хn+10 , хn+m-l0) соответствует решение задачи в исходной форме Хи 0(х10 , х20 ,...,хn0 ), т.е. соответствующее решение получается отбрасыванием дополнительных переменных.
Аналогичное соответствие получается для оптимальных решений исходной и канонической форм.
Так как однородная форма является исходной формой с ограничениями типа меньше или равно, то правило соответствия однородной и канонической форм легко выводится из правила соответствия исходной и канонической форм.
Алгоритм перехода от исходной формы к канонической форме
Чтобы от исходной формы перейти к канонической форме необходимо выполнить следующие преобразования:
1. Проверить, все ли переменные неотрицательные:
а) если в исходной форме есть произвольные переменные x j , то их необходимо заменить разностью двух неотрицательных переменных во всех ограничениях и целевой функции:
x j = x j '- x j '' , где x j ' ³0, x j '' ³0
Все переменные становятся неотрицательными. Переход к пункту 2.
|
|
|
б) если в исходной форме все переменные неотрицательные
(x j ³0, j = 1 ¸ n ), то переход от исходной формы к канонической форме начать с пункта 2.
2. Ограничения равенства с неотрицательными переменными оставить без изменений.
3. В левую часть каждого ограничения неравенства ввести одну новую неотрицательную дополнительную переменную х n+i , где n - число основных переменных, i = 1, 2, 3, ...:
а) в ограничения типа меньше или равно дополнительные переменные ввести с коэффициентом "+1";
б) в ограничения типа больше или равно дополнительные переменные ввести с коэффициентом "-1".
Ограничения неравенства заменить на равенства.
4. В целевую функцию дополнительные переменные ввести с нулевыми коэффициентами (+0).
Примечание: дополнительные переменные называют также выравнивающими или балансовыми переменными.
Пример
Перейти от исходной формы записи задачи к канонической:
max Z = 6,2∙X1 - 3,2∙X2 + 4,5∙X3
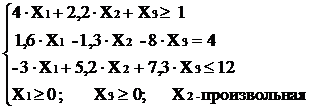
На переменную X2 не наложено условие неотрицательности, а в канонической форме все переменные должны быть неотрицательными,
Поэтому X2 = X' 2- X''2, где X'2 ≥ 0, X''2 ≥ 0.
Получаем:
max Z = 6,2∙X1 - 3,2∙(X’2 – X”2)+ 4,5∙X3
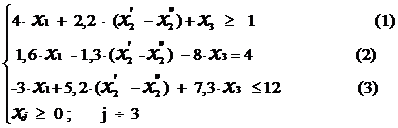
Теперь вводим неотрицательные дополнительные переменные в (1) и (3) ограничения, так как они неравенства. Смотрим, сколько всего основных переменных в системе? n = 3. Следовательно, дополнительной переменной в (1) ограничении будет переменная Xn+1 = X3+1 = X4, а в (3) ограничении будет переменная Xn+2 = X3+2 = X5.
|
|
|
Получим систему:
max Z = 6,2∙X1 - 3,2∙X’2 + 3,2∙X”2 + 4,5∙X3 + 0∙X4 + 0∙X5
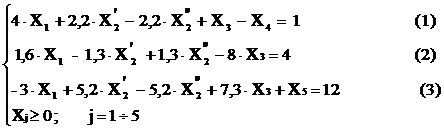
Получили каноническую форму записи задачи, так как все ограничения равенства и все переменные неотрицательные.
Дата добавления: 2018-04-05; просмотров: 337; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
