Л А Б О Р А Т О Р Н А Я Р А Б О Т А № 2

СОСТАВЛЕНИЕ ВЫБОРОЧНОГО УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ РЕГРЕССИИ

ЗАДАНИЕ

1. По заданной выборке двумерной случайной величины: срок хранения и содержание питательных веществ, определить оценки основных числовых характеристик распределения генеральной совокупности (выборочное среднее 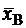, выборочную дисперсию 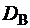и выборочный коэффициент корреляции ).

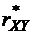2. Составить выборочное уравнение прямой линии регрессии.

КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

Выборочное уравнение регрессии. Зависимость условного математического ожидания 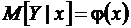называют функций (линией) регрессии Y на Х. Соответственно зависимость 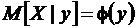называется функций (линией) регрессии Х на Y.

В качестве оценок условных математических ожиданий принимают условные средние, которые находят по данным наблюдения, то есть по выборке.

Условным средним 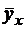называют среднее арифметическое наблюдавшихся значений Y, соответствующих 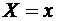. Так если при 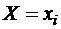величина Y приняла k значений 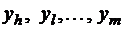, то

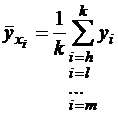Например, если при 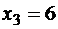величина Y приняла значения 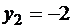; ; 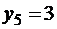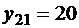, то .

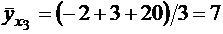Аналогичным образом определяется условное среднее 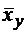– среднее арифметическое наблюдавшихся значений Х, соответствующих .

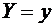Условное математическое ожидание, например, 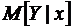, является функцией х. Следовательно, и его оценка, то есть условное среднее 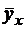, также будет функцией х. Уравнение

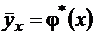
называют выборочным уравнением регрессии Y на Х; функцию 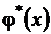называют выборочной регрессией Y на Х, а ее график – выборочной линией регрессии Y на Х. Аналогично уравнение

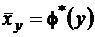
называют выборочным уравнением регрессии Х на Y; функцию 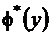называют выборочной регрессией Х на Y, а ее график – выборочной линией регрессии Х на Y.

При исследовании статистических зависимостей обычно задаются из каких-либо соображений видом функци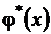й или 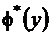. Таким образом, анализ выборочных данных направлен на определение параметров функци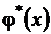й или .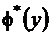

Отыскание параметров линейных уравнений регрессии. Пусть изучается система двух случайных величин 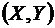. В результате п независимых опытов получены п пар чисел 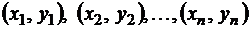. Найдем по данным наблюдений выборочное уравнение прямой линии регрессии. Для определенности будем искать уравнение

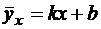(1)

регрессии Y на Х. Коэффициент k в (1) называют выборочным коэффициентом регрессии Y на Х и обозначают как 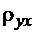. Ясно, что 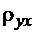является оценкой коэффициента регрессии генеральной совокупности.

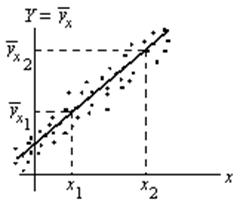
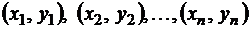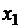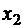Очевидно, прямая линия регрессии должна так расположиться среди точек , построенных по данным наблюдений, чтобы для каких-либо и значения Y на прямой линии регрессии соответствовали условным средним 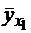и 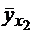. Иными словами, прямая (1) должна проходить через средние значения случайной величины Y, которые она принимает при всех возможных значениях второй случайной величины Х (рис.1).

Если не проводить группировку выборочных данных, то с учетом введенного обозначения уравнение (1) можно записать в виде

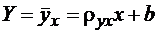. (2)

Подберем параметры 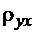и b уравнения (2) так, чтобы точки 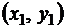, , 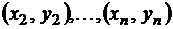построенные по данным наблюдений, лежали как можно ближе к прямой (2). Для уточнения понятия «как можно ближе» введем параметр

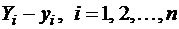имеющий смысл отклонения вычисленного по уравнению (2) значения 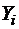, соответствующего наблюдаемому значению 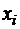, от наблюдаемого значения 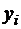пары .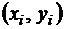

Рис.1

Будем подбирать параметры 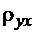и b так, чтобы сумма квадратов отклонений для всех точек 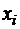была минимальной. Такой подход к обработке выборочных данных называется методом наименьших квадратов. Так как каждое отклонение зависит от отыскиваемых параметров, то и сумма квадратов отклонений будет функцией 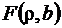определяемых параметров 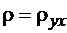и b. При использовании метода наименьших квадратов для определения параметров 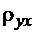и b полученная прямая (2) называется выборочной среднеквадратической линией регрессии.

Таким образом, для определения параметров выборочной среднеквадратической прямой линии регрессии необходимо рассмотреть функцию

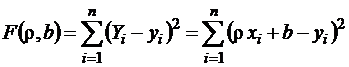, (3)

и найти такие значения параметров 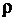и b, при которых функция двух переменных 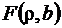(3) достигает минимума.

Для отыскания значений аргументов функции двух переменных, при которых функция достигает экстремума, необходимо решить систему двух уравнений

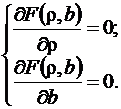
После дифференцирования (3) получаем

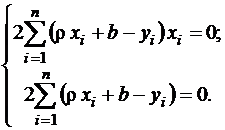
После элементарных преобразований получаем систему двух линейных уравнений относительно 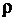и b:

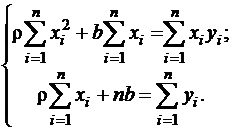(4)

Для решения (4) по правилу Крамера находим определители

;

; .

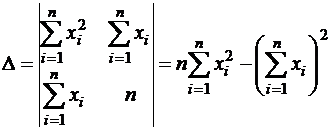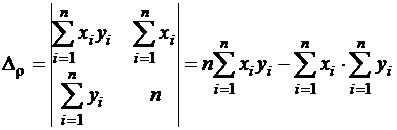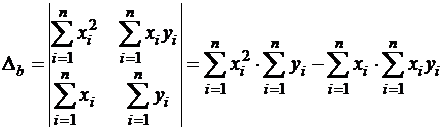Таким образом,

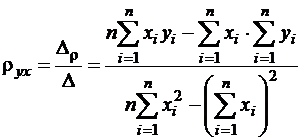; (5)

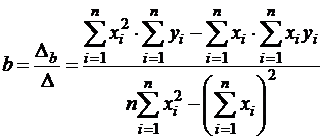Аналогичным образом можно найти параметры выборочного уравнения регрессии Х на Y, применяя метод наименьших квадратов к зависимости

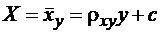где 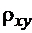– выборочный коэффициент регрессии Х на Y.

Очевидно, систему уравнений (4) можно представить в другом виде. Так как

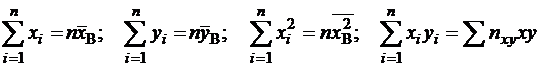, (6)

где введено обозначение 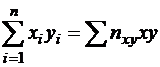, учитывающее, что пара чисел 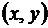наблюдалась 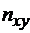раз, то систему (4) можно записать как

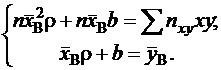(7)

Из второго уравнения системы (7) находим 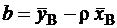. Подставляя это значение параметра b в исходное уравнение 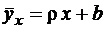, получаем

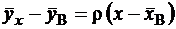. (8)

Преобразуем решение для 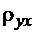(5) с учетом обозначений (6):

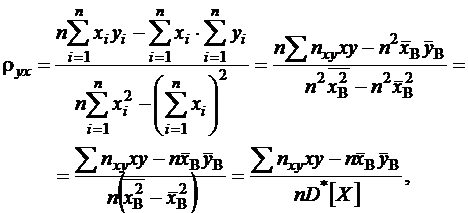(9)

где 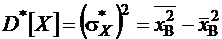– выборочная дисперсия. После умножения обеих частей (9) на дробь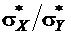

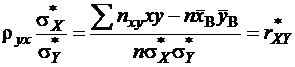где 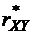– выборочный коэффициент корреляции. Таким образом,

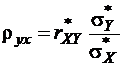. (10)

Подставляя (10) в (8), получаем окончательный вид уравнения прямой линии регрессии Y на Х

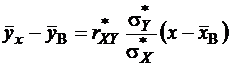. (11)

Заметим, что аналогичным образом можно найти уравнение прямой линии регрессии Х на Y, которое имеет вид

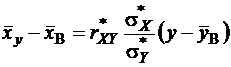, (12)

i	X	Y	XY	X ²	Y ²
1	1,8	43	77,4	3,24	1849
2	2,6	44	114,4	6,76	1936
3	1,5	35	52,5	2,25	1225
4	2,1	40	84	4,41	1600
5	2,3	42	96,6	5,29	1764
6	1,6	37	59,2	2,56	1369
7	1	32	32	1	1024
8	1,2	31	37,2	1,44	961
9	1,4	36	50,4	1,96	1296
10	1,7	39	66,3	2,89	1521

Таблица 1

Таким образом, уравнения регрессии (11) или (12) характеризуют линейную связь условных средних системы двух случайных величин с их возможными значениями. Параметрами зависимости являются выборочные средние и среднеквадратические отклонения случайных величин Х и Y, а также выборочный коэффициент корреляции.

Пример. Произведена экспертиза томатов. Зарегистрированы сроки хранения Х (в часах) и одновременно записаны соответствующие значения содержания группы определяющих витаминов Y (в в мг). Зарегистрированные значения величин 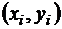приведены в табл.1. Найти оценки для числовых характеристик системы 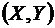. Составить выборочное уравнение прямой линии регрессии Y на Х.

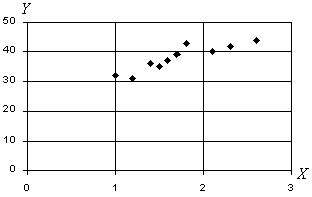
Решение. Для наглядности пары точек 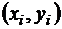нанесены на график (рис.2). Расположение точек на графике уже свидетельствует о наличии определенной зависимости (положительной корреляции) между Х и Y.

Известным способом определяются выборочные средние величин Х и Y:

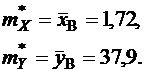
Эти величины рассчитываются как средние арифметические второго и третьего столбцов табл.1.

Для определения дисперсий величин Х и Y сначала целесообразно вычислить их вторые выборочные начальные моменты:

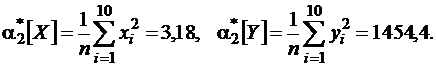
Эти величины рассчитываются как средние арифметические пятого и шестого столбцов табл.1.

Имея эти данные, можно определить выборочную дисперсию величин Х и Y:

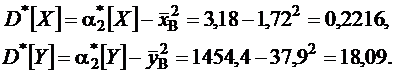
Выборочные среднеквадратические отклонения соответственно равны

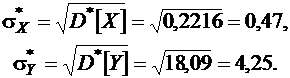
Рис.2

Определяем выборочный второй смешанный момент 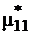. Для этого находится среднее арифметическое произведений пар 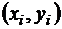, которые помещены в четвертом столбце табл.1, из которого вычитается произведение выборочных средних:

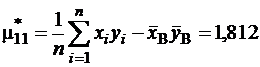Наконец, в соответствии с (1) вычисляется выборочный коэффициент корреляции

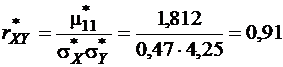Полученное достаточно большое значение 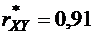указывает на наличие существенной связи между Х и Y.

Подставив вычисленные значения числовых характеристик в (11), получаем уравнение регрессии Y на Х

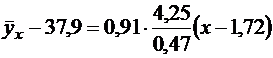После элементарных преобразований

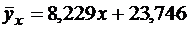Очевидным способом, используя вычисленные числовые характеристики, можно построить уравнение регрессии Х на Y.

Дата добавления: 2018-04-05; просмотров: 366; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 Следующая ⇒

Мы поможем в написании ваших работ!