Основные распределения в статистике
Московский Авиационный Институт
(Государственный Технический Университет)
Курсовая работа по теории вероятностей и математической статистике
Выполнил: студент группы 07-206
Леонов А.А.
Принял:
Мирошкин В.Л.
Теоретическая часть.
Некоторые сведения из теории вероятностей
Под случайной величиной (СВ) понимают величину, которая в результате опыта принимает то или иное значение, причем неизвестно заранее, какое именно.
Вероятностный смысл математического ожидания (МО) состоит в том, что оно является средним значением СВ
Дисперсией (рассеянием) СВ называется математическое ожидание квадрата ее отклонения от своего математического ожидания. Характеризует разброс значений СВ относительно ее МО
Функцией распределения СВ Х называется функция F(x), которая для любого x 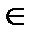 R равна вероятности события { X < x }
R равна вероятности события { X < x }
Квантилью уровня p СВ Х называется решение уравнения FX(xp) ≤ p, т.е. такое xp при котором вероятность события { X < xp } не превышает p
Основные непрерывные распределения
Равномерное распределение
Определение 1.1 СВ Х распределена равномерно на отрезке [a,b] (X~R(a;b)), если плотность вероятности имеет вид


Свойства R(a;b)
1) Функция распределения имеет вид (рис. 2)


2) МО и дисперсия по определению равны

Графики функций f(x) и F(x)приведены на рисунке.
| a |
| 0 |
| b |
| f(x) |

|
| x |
| a |
| 0 |
| b |
| F(x) |
| x |
| 1 |
|
|
|
Нормальное распределение
Определение 1. 3. СВ X имеет нормальное (гауссовское) распределение с параметрами т и σ2 > 0, т.е. X~N(m;σ2), если

При этом СВ называется нормальной (гауссовской). График плотности нормального распределения, называемый кривой Гаусса, имеет единственный максимум в точке х = т
| m2>m1 |
| σ2>σ1 |
| f(x) |
| m1 |
| m2 |
| 0 |
Свойства N(m;σ2)
1) функция распределения СВ X ~N(m;σ2) имеет вид

Функцию распределения можно выразить через функцию стандартного нормального распределения следующим образом:
 , где
, где 
2) МО и дисперсия СВ X ~ N(m;σ2) равны
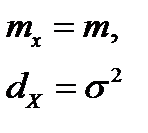
Вычисления, связанные с нормальным распределением, чаще осуществляются не через  ,а через функцию Лапласа
,а через функцию Лапласа

как более удобную, в частности тем, что она является нечетной



Следует, однако помнить что функция 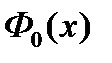 (в отличии от
(в отличии от  ) не является функцией распределения.
) не является функцией распределения.
Функции  связаны соотношением
связаны соотношением
 .
.
 5) Нормально распределенная СВ с большой вероятностью принимает значения, близкие к своему МО, что описывается «правилом к сигм»:
5) Нормально распределенная СВ с большой вероятностью принимает значения, близкие к своему МО, что описывается «правилом к сигм»:


|
|
|
Математическая статистика – наука о математических методах, позволяющих по статистическим данным, например по реализациям случайной величины (СВ), построить теоретико-вероятностную модель исследуемого явления. Задачи математической статистики являются, в некотором смысле, обратными к задачам теории вероятностей. Центральным понятием математической статистики является выборка.
Определение 1.Однородной выборкой (выборкой) объема n при n  1 называется случайный вектор Zn=col(X1,…,Xn), компоненты которого Xi, i=
1 называется случайный вектор Zn=col(X1,…,Xn), компоненты которого Xi, i= 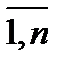 , называемые элементами выборки, являются независимыми СВ с одной и той же функцией распределения F(x). Будем говорить, что выборка Zn соответствует функции распределения F(x).
, называемые элементами выборки, являются независимыми СВ с одной и той же функцией распределения F(x). Будем говорить, что выборка Zn соответствует функции распределения F(x).
Определения 2.Реализацией выборки называется неслучайный вектор zn=col(x1,…,xn), компонентами которого являются реализации соответствующих элементов выборки Xi, i= 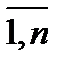 .
.
Из этих определений вытекает, что реализацию выборки zn можно также рассматривать как последовательность x1,…,xn из n реализаций одной и той же СВ X, полученных в серии из n независимых одинаковых опытов, проводимых в одинаковых условиях. Поэтому можно говорить, что выборка Zn порождена наблюдаемой СВ X, имеющей распределение Fx(x)=F(x).
|
|
|
Определение 3.Если компоненты вектора Zn  независимы, но их распределения F1(x1),…,Fn(xn) различны, то такую выборку называют неоднородной.
независимы, но их распределения F1(x1),…,Fn(xn) различны, то такую выборку называют неоднородной.
Определение 4.Множество S всех реализаций выборки Zn называется выборочным пространством.
Выборочное пространство может быть всем n-мерным евклидовым пространством или его частью, если СВ X непрерывна, а также может состоять из конечного или счетного числа точек из Rn, если СВ X дискретна.
На практике при исследовании конкретного эксперимента распределения F1(x1),…,Fn(xn) СВ X1,…,Xn редко бывают известны полностью. Часто априори (до опыта) можно лишь утверждать, что распределение FZn(zn)=F1(x1),…Fn(xn) случайного вектора Zn принадлежит некоторому классу (семейству) F.
Определение 5. Пара (S,F) называется статистической моделью описания серии опытов, порождающих выборку Zn.
Определение 6.Если распределение FZn(zn,Ө) из класса F определены с точностью до некоторого векторного параметра Ө 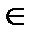 Θ
Θ  IRs, то такая статистическая модель называется параметрической и обозначается (S Ө, FZn(zn, Ө)), Ө
IRs, то такая статистическая модель называется параметрической и обозначается (S Ө, FZn(zn, Ө)), Ө 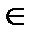 Θ
Θ  Rs.
Rs.
В некоторых случаях выборочное пространство может не зависеть от неизвестного параметра Ө распределения FZn(zn,Ө).
Определение 7.СВ Z=φ(Zn), где φ(Zn) – произвольная функция, определенная на выборочном пространстве S и не зависящая от распределения FZn(zn,Ө), называется статистикой.
|
|
|
Определение 8. Упорядочим элементы реализации выборки  ,...,
,...,  по возрастанию
по возрастанию  ,где верхний индекс соответствует номеру элемента в упорядоченной последовательности. Обозначим через
,где верхний индекс соответствует номеру элемента в упорядоченной последовательности. Обозначим через 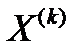 ,
,  ,случайные величины, которые при каждой реализации
,случайные величины, которые при каждой реализации  выборки
выборки  принимают
принимают  -е(по верхнему номеру) значения
-е(по верхнему номеру) значения  .Упорядоченную последовательность СВ
.Упорядоченную последовательность СВ  называю вариационным рядом.
называю вариационным рядом.

Выборочные моменты
Пусть имеется выборка Zn = = col(X1, ...,Хп), которая порождена СВ X с функцией распределения FХ (x).
Определение 4.1. Для выборки Zn объема п выборочными начальными и центральными моментами порядка r СВ X называются следующие СВ:

Определение 4.2. Выборочным средним и выборочной дисперсией СВ X называются соответственно

Пусть существуют исследуемые моменты νг, μТ. Тогда справедливы следующие свойства.
Свойства выборочных моментов 
1)  для любого
для любого  и для всех г = 1,2,
и для всех г = 1,2,
2)  , где
, где  .
.
3)  .
.
Основные распределения в статистике
Распределение хи-квадрат
Определение 2. 1. Пусть Uk,  , - набор из n независимых нормально распределенных СВ,
, - набор из n независимых нормально распределенных СВ,  ~N(0;1). Тогда СВ
~N(0;1). Тогда СВ

Имеет распределение хи-квадрат с n степенями свободы, что обозначается Xn~χ2(n)
Свойства распределения хи-квадрат χ2(n)
1) СВ Xn имеет следующую плотность распределения:
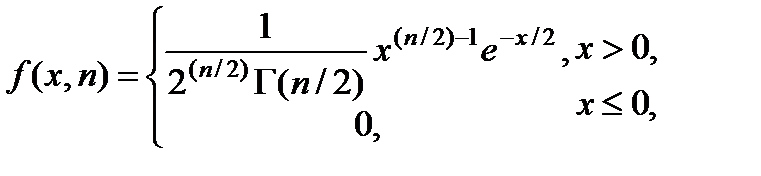
где 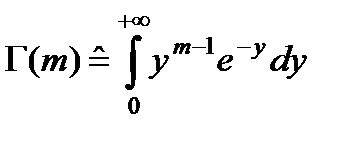 - гамма-функция.
- гамма-функция.
2) СВ Xn~χ2(n) имеет моменты:



3) Сумма любого числа m независимых СВ Xk,  , имеющих распределение хи-квадрат с nk степенями свободы, имеет распределение хи-квадрат с
, имеющих распределение хи-квадрат с nk степенями свободы, имеет распределение хи-квадрат с 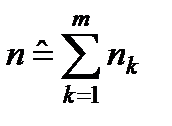 степенями свободы.
степенями свободы.
4) Распределение хи-квадрат обладает свойством асимптотической нормальности:
 при
при 
где СВ U имеет распределение N(0;1). Это означает, что при достаточно большом объеме n выборки можно приближенно считать Xn~N(n; 2n). Фактически эта аппроксимация имеет место уже при n > 30.
Распределение Стьюдента
Определение 2.2. Пусть U и  — независимые СВ, U ~N(0; 1),
— независимые СВ, U ~N(0; 1),  ~ χ2(n) . Тогда СВ
~ χ2(n) . Тогда СВ  имеет распределение Стьюдента с n степенями свободы, что обозначают как
имеет распределение Стьюдента с n степенями свободы, что обозначают как  ~S(n).
~S(n).
Свойства распределения Стьюдента S(n)
1) СВ  имеет плотность распределения
имеет плотность распределения
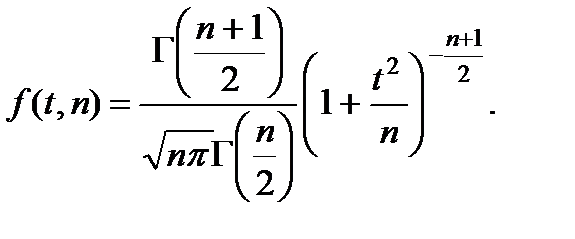
2) СВ  имеет МО, равное М[Тn] = 0 для всех n
имеет МО, равное М[Тn] = 0 для всех n  2, и дисперсию D[
2, и дисперсию D[  ] = n/(n - 2) при n > 2. При n = 2 дисперсия
] = n/(n - 2) при n > 2. При n = 2 дисперсия  .
.
3) Можно показать, что при  распределение S (n) асимптотически нормально, т. е.
распределение S (n) асимптотически нормально, т. е.  , где СВ U имеет распределение N(0; 1). При n
, где СВ U имеет распределение N(0; 1). При n  30 распределение Стьюдента S (n) практически не отличается от N(0; 1).
30 распределение Стьюдента S (n) практически не отличается от N(0; 1).
Точечные оценки.
Параметром распределения  СВ X называется любая числовая характеристика этой СВ (математическое ожидание, дисперсия и т.п.) или любая константа, явно входящая в выражение для функции распределения.
СВ X называется любая числовая характеристика этой СВ (математическое ожидание, дисперсия и т.п.) или любая константа, явно входящая в выражение для функции распределения.
В общем случае будем предполагать, что параметр распределения θможет быть векторным, т. е. 
В случае параметрической статистической модели ( 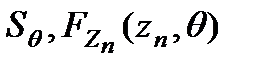 ) таким параметром распределения может служить неизвестный вектор
) таким параметром распределения может служить неизвестный вектор  , характеризующий распределение
, характеризующий распределение  .
.
Пусть имеется выборка Zn = со1(X1, ... ,Хп) с реализацией zn = col(x1, ...,хп).
Точечной (выборочной) оценкой неизвестного параметра распределения  называется произвольная статистика
называется произвольная статистика  (Zn), построенная по выборке Zn и принимающая значения в множестве
(Zn), построенная по выборке Zn и принимающая значения в множестве  .
.
Реализацию  (zn) оценки
(zn) оценки  (Zn) принимают, как правило, за приближенное значение неизвестного параметра θ.
(Zn) принимают, как правило, за приближенное значение неизвестного параметра θ.
Дата добавления: 2018-04-05; просмотров: 817; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
