Основные элементарные функции
Степенные с целым показателем 
Показательные y=a^x
Логарифмические
Тригонометрические - tgx, ctgx, sinx, cosx
Обратные тригонометрические (аркфункции) - arctgx, arcctgx, arcsinx, cosx
24. Понятие предела функции в точке и на бесконечности. Односторонние пределы.
Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят). В общем случае необходимо точно указывать способ сходимости функции, для чего вводят базу подмножеств области определения функции, и тогда формулируют определение предела функции по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств.
|
|
|
Поскольку на расширенной вещественной прямой можно построить базу окрестностей бесконечно удалённой точки, то оказывается допустимым описание предела функции при стремлении аргумента к бесконечности, а, также, описание ситуации, когда функция сама стремится к бесконечности (в заданной точке). Предел последовательности (как предел функции натурального аргумента), как раз предоставляет пример сходимости по базе «стремление аргумента к бесконечности».
Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений и всякой его окрестности сколь угодно близко от заданной точки существуют точки, значение функции в которых окажется за пределами заданной окрестности.
Если в некоторой точке области определения функции существует предел и этот предел равен значению в данной функции, то функция оказывается непрерывной (в данной точке).
Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим.
Односторонний предел числовой функции в точке — это специфический предел, подразумевающий, что аргумент функции приближается к указанной точке с определённой стороны (слева или справа). Числовая функция имеет предел в точке тогда и только тогда, когда она имеет в этой точке совпадающие левый и правый пределы.
|
|
|
25. Бесконечно малые и бесконечно большие функции.
Связь между ними.
Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.
Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Исчисление бесконечно малых — вычисления, производимые с бесконечно малыми величинами, при которых производный результат рассматривается как бесконечная сумма бесконечно малых. Исчисление бесконечно малых величин является общим понятием для дифференциальных и интегральных исчислений, составляющих основу современной высшей математики. Понятие бесконечно малой величины тесно связано с понятием предела.
Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если 
или 
, т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
Примеры.
Функция f(x) = tgx – бесконечно малая при x→0.
f(x) = ln (1+x)– бесконечно малая при x→0.
f(x) = 1/x– бесконечно малая при x→∞.
|
|
|
Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.
Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a. Это и есть связь между ними.
26. Свойства бесконечно малых функций. Сравнение бесконечно малых функций. Применение эквивалентных бесконечно малых при отыскании пределов.
Свойства бесконечно малых функций
Пусть 
и 
- бесконечно малые функции при 
, и 
ограничена в некоторой окрестности точки 
. Тогда
1. + - бесконечно малая функция при
2. 
- бесконечно малая функция при
При вычислении пределов широко используется теорема o замене функций на эквивалентные.
Предел отношения двух бесконечно малых функций не изменится, если каждую функцию (или только одну из них) заменить на эквивалентную, т.е. если 
и 
, то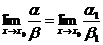 
.
| Эквивалентные бесконечно малые функции
 Мы поможем в написании ваших работ! | ||||