Правило Крамера для решения систем линейных уравнений
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ
1 Векторы. Линейные операции над векторами. Проекция вектора на ось. Свойства проекции.
2 Линейная зависимость векторов. Базис. Разложение вектора по координатному базису.
3 Линейные операции над векторами в координатной форме.
4 Скалярное произведение векторов и его свойства.
5 Координатная форма записи скалярного произведения.
6 Понятие уравнения линии на плоскости. Прямая на плоскости и различные способы ее задания.
7 Взаимное расположение прямых на плоскости.
8 Расстояние от точки до прямой на плоскости.
9 Геометрическое изображение области решений системы линейных неравенств с двумя переменными.
10 Уравнения поверхности и линии в пространстве. Плоскость в пространстве.
11 Взаимное расположение плоскостей.
12 Расстояние от точки до плоскости.
13 Прямая линия в пространстве. Различные способы задания.
14 Взаимное расположение двух прямых в пространстве.
15 Взаимное расположение прямой и плоскости в пространстве. Угол между прямой и плоскостью.
16 Понятие матрицы. Действия над матрицами.
17 Определители 2-го и 3-го порядков и их вычисления.
18 Правило Крамера для решения систем линейных уравнений.
19 Арифметическое n-мерное пространство. Скалярное произведение и его свойства.
20 Ранг матрицы. Обратная матрица и её вычисление.
21 Элементарные преобразования матриц. Формулировка теоремы Кронекера-Капелли.
22 Решение систем линейных уравнений матричным методом.
23 Определение функции и способы её задания. Основные элементарные функции.
24 Понятие предела функции в точке и на бесконечности. Односторонние пределы.
25 Бесконечно малые и бесконечно большие функции. Связь между ними.
26 Свойства бесконечно малых функций. Сравнение бесконечно малых функций. Применение эквивалентных бесконечно малых при отыскании пределов.
27 Первый замечательный предел.
28 Второй замечательный предел.
29 Свойства пределов функции.
30 Непрерывность функции в точке. Различные определения непрерывности в точке.
31 Точки разрыва функции и их классификация.
32 Свойства функций, непрерывных в точке.
33 Свойства функций, непрерывных на отрезке.
34 Задачи, приводящие к понятию производной. Определение производной.
35 Основные правила дифференцирования.
36 Непрерывность дифференцируемой функции.
37 Дифференциал функции. Инвариантность формы дифференциала.
38 Применение дифференциала к приближенным вычислениям.
39 Основные теоремы дифференциального исчисления (теоремы Ферма, Ролля, Лагранжа, Коши, Лопиталя).
40 Формула Тейлора.
41 Применение производной к исследованию функций и построение их графиков (исследования на монотонность, экстремум, выпуклость, асимптоты).
42 Функции нескольких переменных. Предел и непрерывность.
43 Частные производные и полный дифференциал.
44 Достаточные условия экстремума функции 2-х переменных.
45 Понятие производной по направлению и градиента функции нескольких переменных. Связь между ними.
46 Комплексные числа и действия с ними.
47 Первообразная и неопределенный интеграл. Основные свойства неопределенного интеграла.
48 Основные методы интегрирования (непосредственное интегрирование, замена переменной, интегрирование по частям).
49 Задачи, приводящие к понятию определенного интеграла. Определенный интеграл и его свойства.
50 Методы подстановки, интегрирование по частям для вычисления определенного интеграла.
51 Приложение определенных интегралов.
52 Понятия о дифференциальных уравнениях и их решении.
53 Обыкновенные дифференциальные уравнения. Решение обыкновенных дифференциальных уравнений первого порядка и их геометрический смысл.
54 Дифференциальные уравнения первого порядка: с разделяющимися переменными, однородные, линейные.
55 Линейные однородные дифференциальные уравнения второго порядка. Теорема о структуре общего решения.
56 Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами и метод их решения.
57 Линейные неоднородные дифференциальные уравнения второго порядка.
58 Теорема о структуре общего решения.
59 Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью вида
f(x) = eαxPn(x).
60 Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью вида f(x) = eαx (Pn(x) cosβx + Qm(x) sinβx).
61 Числовые ряды. Понятие сходимости числового ряда. Необходимый признак сходимости числового ряда.
62 Геометрический ряд и его сходимость.
63 Гармонический ряд и его сходимость. Понятие о ряде Дирихле (обобщенном гармоническом ряде).
64 Свойства сходящихся рядов.
65 Достаточные признаки сходимости знакоположительных рядов: признаки сравнения, Даламбера, Коши, интегральный признак Коши.
66 Знакопеременные ряды. Абсолютная и условная сходимости.
67 Знакочередующиеся ряды. Признак Лейбница.
68 Функциональные ряды. Понятие о равномерной сходимости функционального ряда.
69 Степенные ряды и их свойства.
1. Векторы. Линейные операции над векторами.
Проекция вектора на ось. Свойства проекции.
Вектором называется направленный отрезок. Если начало вектора находится в точке А, а конец — в точке В, то вектор обозначается АВ. Если же начало и конец вектора не указываются, то его обозначают строчной буквой латинского алфавита а, Ь,с. На рисунке направление вектора изображается стрелкой. Через ВА обозначают вектор, направленный противоположно вектору АВ. Вектор, у которого начало и конец совпадают, называется нулевым и обозначается 0. Его направление является неопределенным. Другими словами, такому вектору можно приписать любое направление. Длиной или модулем вектора называется расстояние между его началом и концом. Записи  и |а| обозначают модули.
и |а| обозначают модули.
Векторы называются коллинеарными, если они параллельны одной прямой, и компланарными, если они параллельны одной плоскости.
Два вектора называются равными, если они коллинеарны, одинаково направлены и равны по длине.
Линейные операции над векторами – сложение, вычитание, умножение на число.
Суммой двух векторов  и
и  называется вектор, который идет из начала вектора
называется вектор, который идет из начала вектора  в конец вектора
в конец вектора  при условии, что вектор
при условии, что вектор  приложен к концу вектора
приложен к концу вектора  (правильно треугольника).
(правильно треугольника).
Сложение многих векторов производится при помощи последовательного применения правила треугольника.


Разностью векторов  и
и  и называют вектор
и называют вектор 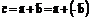 . Второе слагаемое является вектором, противоположным вектору
. Второе слагаемое является вектором, противоположным вектору  по направлению, но равным ему по длине. Таким образом, операция вычитания векторов заменяется на операцию сложения.
по направлению, но равным ему по длине. Таким образом, операция вычитания векторов заменяется на операцию сложения.
Произведением вектора  на действительное число
на действительное число  называется вектор
называется вектор  , модуль которого равен
, модуль которого равен  , а направление совпадает с направлением вектора
, а направление совпадает с направлением вектора  , если
, если  и противоположно направлению вектора
и противоположно направлению вектора  , если
, если  .
.
Единичный вектор, направленный вдоль оси x, обозначается i.
Единичный вектор, направленный вдоль оси y, обозначается j.
Единичный вектор, направленный вдоль оси z, обозначается k.
Вектора i, j, k называются координатными векторами.
Любой вектор a можно разложить по координатным векторам: a=xi+yj+zk.
Коэффициенты разложения определяются единственным образом и называются координатами вектора  в данной системе координат.
в данной системе координат.

Действия над векторами в декартовых координатах: сложение, умножение на число, скалярное произведение
Пусть  ,
,  , тогда
, тогда
сложение 
умножение на число 
скалярное произведение 
2. Линейная зависимость векторов. Базис. Разложение вектора по координатному базису.
Система векторов  называется линейно зависимой, если существует такой набор коэффициентов
называется линейно зависимой, если существует такой набор коэффициентов  , из которых хотя бы один отличен от нуля, что
, из которых хотя бы один отличен от нуля, что 
Свойство 1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы.
Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.
Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.
Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.
Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.
Свойство 6. Любые 4 вектора линейно зависимы.
Любые три упорядоченные некомпланарные вектора  образуют базис в пространстве.
образуют базис в пространстве.
Выражение  называется разложением вектора
называется разложением вектора  по базису
по базису  . Разложение вектора в базисе единственно. Числа
. Разложение вектора в базисе единственно. Числа  называются координатами вектора
называются координатами вектора  в базисе
в базисе  .
.
3. Линейные операции над векторами в координатной форме
Любой вектор a можно разложить по координатным векторам: a=xi+yj+zk.
Коэффициенты разложения определяются единственным образом и называются координатами вектора  в данной системе координат.
в данной системе координат.

Единичный вектор, направленный вдоль оси x, обозначается i.
Единичный вектор, направленный вдоль оси y, обозначается j.
Единичный вектор, направленный вдоль оси z, обозначается k.
Действия над векторами в декартовых координатах: сложение, умножение на число, скалярное произведение
Пусть  ,
,  , тогда
, тогда
сложение 
умножение на число 
скалярное произведение 
4. Скалярное произведение векторов и его свойства.
Скалярным произведением двух векторов называется скаляр (число), равное произведению длин этих векторов на косинус угла между ними.

где  - угол между векторами,
- угол между векторами,  ,
,  - модули (длины) векторов
- модули (длины) векторов
Скалярное произведение векторов можно выразить также формулами

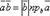
Скалярное произведение  называется скалярным квадратом вектора и обозначается символом
называется скалярным квадратом вектора и обозначается символом 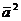 . Скалярный квадрат вектора равен квадрату его модуля:
. Скалярный квадрат вектора равен квадрату его модуля:  .
.
Если векторы заданы своими координатами:  ,
,  , то их скалярное произведение можно вычислить по формуле:
, то их скалярное произведение можно вычислить по формуле: 
Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов: 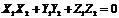
Угол между векторами (сторонами, прямыми): 
Длина (модуль) вектора:  ,
, 
Свойства скалярного произведения:
1.  (коммутативность)
(коммутативность)
2. 
3. 
5. Координатная форма записи скалярного произведения.
Скалярным произведением двух векторов называется скаляр (число), равное произведению длин этих векторов на косинус угла между ними.

где  - угол между векторами,
- угол между векторами,  ,
,  - модули (длины) векторов
- модули (длины) векторов
Скалярное произведение  называется скалярным квадратом вектора и обозначается символом
называется скалярным квадратом вектора и обозначается символом 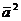 . Скалярный квадрат вектора равен квадрату его модуля:
. Скалярный квадрат вектора равен квадрату его модуля:  .
.
Если векторы заданы своими координатами:  ,
,  , то их скалярное произведение можно вычислить по формуле:
, то их скалярное произведение можно вычислить по формуле: 
Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов: 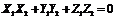
Свойства скалярного произведения:
1. 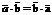 (коммутативность)
(коммутативность)
2. 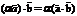
3. 
6. Понятие уравнения линии на плоскости. Прямая на плоскости и различные способы ее задания.
Любая прямая на плоскости может быть задана уравнением первого порядка, называемым общим уравнением прямой  , где
, где  - нормальный вектор прямой.
- нормальный вектор прямой.
Уравнение прямой с угловым коэффициентом: 
Угловой коэффициент прямой (тангенс угла наклона прямой к положительному направлению оси Ох): 
Уравнение прямой «в отрезках», т.е. прямая отсекает на оси Ох отрезок 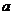 , а на оси Оу отрезок
, а на оси Оу отрезок  :
:  . Данное уравнение удобно для построения прямой, но не подходит для прямых, проходящих через начало координат.
. Данное уравнение удобно для построения прямой, но не подходит для прямых, проходящих через начало координат.
Уравнение прямой в каноническом виде (прямая проходит через точку  , параллельно вектору
, параллельно вектору  ):
): 
Параметрические уравнения прямой получаются из канонического уравнения: 
 , t – параметр
, t – параметр
Чтобы записать уравнение прямой плоскости, можно использовать следующие формулы.
Уравнение прямой, проходящей через две точки: 
Уравнение прямой, проходящей через точку  в данном направлении:
в данном направлении: 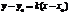
Уравнение прямой, проходящей через точку  , параллельно вектору
, параллельно вектору  :
: 
Уравнение прямой, проходящей через точку  , перпендикулярно вектору
, перпендикулярно вектору  :
:

7. Взаимное расположение прямых на плоскости.
Взаимное расположение прямых на плоскости может быть следующим: прямые могут пересекаться под каким либо углом, либо быть параллельными, либо перпендикулярными.
Угол между двумя прямыми:
* если прямые заданы в общем виде  и
и  , то угол между ними равен углу между их нормальными векторами
, то угол между ними равен углу между их нормальными векторами  и
и  :
: 
* если прямые заданы в виде с угловым коэффициентом, то угол находится на основе их угловых коэффициентов:  .
.
Условия параллельности прямых:
* если прямые заданы общем виде  и
и  , то условием их параллельности является пропорциональность координат их нормальных векторов:
, то условием их параллельности является пропорциональность координат их нормальных векторов: 
* если прямые заданы в виде с угловым коэффициентом  и
и  , то условием их параллельности является равенство их угловых коэффициентов
, то условием их параллельности является равенство их угловых коэффициентов 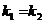 .
.
Условия перпендикулярности прямых:
* если прямые заданы общем виде  и
и  , то скалярное произведение их нормальных векторов равно 0:
, то скалярное произведение их нормальных векторов равно 0: 
* если прямые заданы в виде с угловым коэффициентом  и
и  , то
, то 
8. Расстояние от точки до прямой на плоскости
Вычисляется по перпендикуляру как расстояние от точки 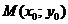 до прямой, заданной в общем виде
до прямой, заданной в общем виде
 :
:  . Числитель формулы берется по модулю, чтобы значение расстояния было всегда положительным числом. По такой формуле вычислят, например, длину высоты в треугольнике – расстояние от точки до противолежащей стороны.
. Числитель формулы берется по модулю, чтобы значение расстояния было всегда положительным числом. По такой формуле вычислят, например, длину высоты в треугольнике – расстояние от точки до противолежащей стороны.
9. Геометрическое изображение области решений системы неравенств с двумя переменными.
Системой линейных алгебраических нестрогих неравенств с двумя неизвестными называется система неравенств вида
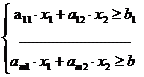
Числа называются  коэффициентами системы;
коэффициентами системы;  – свободными членами;
– свободными членами;  – неизвестными.
– неизвестными.
Решением системы неравенств называется упорядоченная пара чисел  такая, что после замены неизвестных соответственно числами каждое неравенство системы превращается в верное числовое неравенство. Система неравенств называется совместной, если она имеет хотя бы одно решение. Если система неравенств не имеет ни одного решения, то она называется несовместной.
такая, что после замены неизвестных соответственно числами каждое неравенство системы превращается в верное числовое неравенство. Система неравенств называется совместной, если она имеет хотя бы одно решение. Если система неравенств не имеет ни одного решения, то она называется несовместной.
Каждое неравенство системы задает некоторую область в двухмерном пространстве координат. Знак системы означает, что нужно просто найти пересечение этих самых множеств. Для решения чаще всего используют графический метод. При этом строят вначале граничные прямые, затем определяют, какую полуплоскость относительно этих прямых определяют неравенства (подставляют пробную точку), затем находят область решений общую область, ограничиваемую всеми неравенствами.
10. Уравнения поверхности и линии в пространстве. Плоскость в пространстве.
Если в трехмерном пространстве задана произвольная плоскость  и зафиксирована прямоугольная Декартова система координат
и зафиксирована прямоугольная Декартова система координат  , то плоскость
, то плоскость  определяется относительно этой системы уравнением первой степени:
определяется относительно этой системы уравнением первой степени:
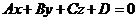 (1) - общее уравнение плоскости
(1) - общее уравнение плоскости
Где А, В, С – постоянные, причем хотя бы одна из них 
Ур-е (1) имеет хотя бы одно решение, т.е. существует точка  , удовлетворяющая уравнению (1)
, удовлетворяющая уравнению (1)  (2)
(2)
Вычитая из (1) уравнения (2), получим
 (3) – нормальное уравнение плоскости, проходящей через точку
(3) – нормальное уравнение плоскости, проходящей через точку  , перпендикулярно вектору
, перпендикулярно вектору  (нормальный вектор плоскости).
(нормальный вектор плоскости).
Записать уравнение плоскости можно, используя формулы:
Уравнение плоскости, проходящей через точку  , перпендикулярно вектору
, перпендикулярно вектору  :
: 
Уравнение плоскости, проходящей через 3 точки: 
Прямая в пространстве может быть задана как линия пересечения двух плоскостей

Записать уравнение плоскости можно, используя формулы.
Уравнение прямой, проходящей через 2 точки:

Уравнение прямой в каноническом виде:
 ,
, 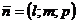 -направляющий вектор
-направляющий вектор
Параметрические уравнения прямой получаются из канонического уравнения: 
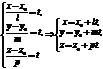 t – параметр
t – параметр
11. Взаимное расположение плоскостей
Если плоскости заданы уравнениями  и
и  (нормальные векторы плоскостей
(нормальные векторы плоскостей 
 ), то взаимное расположение двух плоскостей может быть:
), то взаимное расположение двух плоскостей может быть:
1) плоскости пересекаются, если нормальные векторы плоскостей  и
и  не параллельны
не параллельны

2) плоскости параллельны (но не совпадают), если  (
(  ),
), 
3) совпадают если  (
(  ),
), 

Угол между плоскостями рассчитывается как угол между их нормальными векторами: 
Необходимое и достаточное условие перпендикулярности двух плоскостей – равенство нулю скалярного произведения их нормальных векторов: 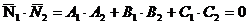
12. Расстояние от точки до плоскости
Расстояние от точки  до плоскости, заданной в общем виде
до плоскости, заданной в общем виде  вычисляется по формуле:
вычисляется по формуле: 
13. Прямая линия в пространстве. Различные способы задания.
Уравнение прямой, проходящей через 2 точки:

Уравнение прямой в каноническом виде:
 ,
, 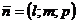 -направляющий вектор
-направляющий вектор
Параметрические уравнения прямой:  , t –– параметр
, t –– параметр
Прямая как линия пересечения двух плоскостей: 
14. Взаимное расположение двух прямых в пространстве
Прямые в пространстве могут пересекаться (тогда они лежат в одной плоскости), могут быть параллельными (тогда они также лежат в одной плоскости) или скрещиваться.
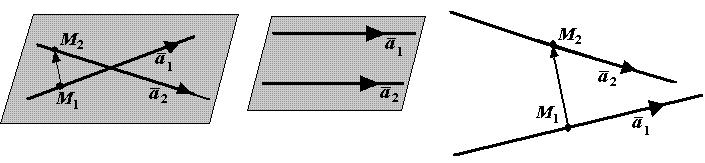
Две прямые пересекаются тогда и только тогда, когда векторы
 ,
,  и
и  компланарны, и при этом не параллельны векторы
компланарны, и при этом не параллельны векторы  и
и  , т.е. когда
, т.е. когда  и
и 
Две прямые параллельны тогда и только тогда, когда параллельны векторы  и
и  , т.е. когда существует число λ такое что,
, т.е. когда существует число λ такое что,  ,
, 
 .
.
Две прямые скрещиваются тогда и только тогда, когда не компланарны векторы и при этом не параллельны векторы  и
и  , т.е. когда
, т.е. когда 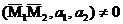 и
и 
15. Взаимное расположение прямой и плоскости в пространстве. Угол между прямой и плоскостью.
Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке.
Пусть плоскость  задана общим уравнением
задана общим уравнением  , а прямая L задана каноническими уравнениями
, а прямая L задана каноническими уравнениями  или параметрическими уравнениями
или параметрическими уравнениями  , в которых
, в которых  - координаты нормального вектора плоскости
- координаты нормального вектора плоскости  ,
,  - произвольная фиксированная точка прямой L,
- произвольная фиксированная точка прямой L,  - направляющий вектор прямой . Тогда:
- направляющий вектор прямой . Тогда:
1.если  , то прямая L пересекает плоскость в точке
, то прямая L пересекает плоскость в точке 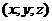 , координаты которой можно найти из системы уравнений
, координаты которой можно найти из системы уравнений


2.если  и
и  , то прямая лежит на плоскости
, то прямая лежит на плоскости

3.если  и
и  , то прямая параллельна плоскости.
, то прямая параллельна плоскости.

16. Понятие матрицы. Действия над матрицами.
Матрицей размеров  называется прямоугольная таблица, составленная из
называется прямоугольная таблица, составленная из  элементов некоторого множества. Матрица, элементами которой являются числа, называется числовой.
элементов некоторого множества. Матрица, элементами которой являются числа, называется числовой.
Матрица с равным количеством строк и столбцов называется квадратной.
Операции сложения и вычитания проводят над матрицами одинаковых размеров. В этом случае проводят сложение или вычитание элементов матриц, стоящих на одинаковых местах.
Сложение матриц обладает свойствами:
1.  +
+  =
=  +
+  ; 2. (
; 2. (  +
+  )+
)+  =
=  +(
+(  +
+  );
);
3.  + 0 =
+ 0 =  ; 4. (-
; 4. (-  )+(
)+(  )=0
)=0
Умножение матрицы на число 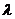 - каждый элемент матрицы умножается на это число.
- каждый элемент матрицы умножается на это число.
Очевидны следующие свойства:
1. 1*А=А; 2.  ;
;
3.  4.
4.  .
.
Транспонировать матрицу - поменять местами строки и столбцы.
Произведением матрицы  на матрицу
на матрицу  называется матрица
называется матрица  , элементы которой находятся по формуле
, элементы которой находятся по формуле  (каждую строку матрицы А умножаем на каждый столбец матрицы В). В ответе получаем матрицу С, у которой число строк m матрицы слева (А), число столбцов k матрицы справа (В).
(каждую строку матрицы А умножаем на каждый столбец матрицы В). В ответе получаем матрицу С, у которой число строк m матрицы слева (А), число столбцов k матрицы справа (В).

Свойства произведения матриц:
1. Ассоциативность: 
2. Легко проверить, что если Е – единичная матрица тождественного оператора, то AE=EA=A.
3. Дистрибутивность произведения операторов:

Единичная матрица – квадратная матрица, у которой на главной диагонали 1, остальные элементы 0.
17. Определители 2-гр и 3-го порядков и их вычисления
Определителем 2-го порядка называется величина

Числа  называются элементами определителя (детерминанта).
называются элементами определителя (детерминанта).
Свойства определителя:
1) Величина определителя не меняется, если у него заменить строки соответствующими столбцами:
2) меняет знак, если у него переменить местами строки (столбцы)
3) увеличивается в k раз, если элементы какого-либо его столбца или строки увеличить в k раз
4) равна нулю, если элементы какого-либо его столбца или строки равна нулю
5) равна нулю, если элементы двух строк или столбцов пропорциональны
Для определителей третьего порядка свойства 1)-5) сохраняются.
Число

записываемое в форме
| (3) |


называется определителем 3-го порядка. Число  называется элементом определителя, i – номер строки, j – номер столбца определителя. Элементы
называется элементом определителя, i – номер строки, j – номер столбца определителя. Элементы  образуют главную диагональ определителя, а элементы
образуют главную диагональ определителя, а элементы  - побочную.
- побочную.
Определитель 3-го порядка вычисляют по «правилу треугольников».
Произведения элементов, стоящих на главной диагонали и произведения элементов, стоящих в вершинах равнобедренных треугольников с основаниями, параллельными главной диагонали, берутся со знаком «+»;
произведения элементов, стоящих на побочной диагонали и произведения элементов, стоящих в вершинах равнобедренных треугольников с основаниями, параллельными побочной диагонали, берутся со знаком «-».

Правило Крамера для решения систем линейных уравнений.
Рассмотрим систему n линейных уравнений с n неизвестными (1)

Ее решением называется любая совокупность значений  ,
, 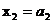 , …,
, …,  ,…, при подстановке которых все уравнения системы обращаются в тождества. Предположим, что определитель этой системы
,…, при подстановке которых все уравнения системы обращаются в тождества. Предположим, что определитель этой системы 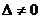 , тогда решение системы вычисляется по формуле:
, тогда решение системы вычисляется по формуле:
 ,
, 
Где  - главный определитель системы, получаемый из коэффициентов при неизвестных;
- главный определитель системы, получаемый из коэффициентов при неизвестных;
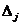 - вспомогательные определители, получаемые из главного заменой j-го столбца столбцом свободных членов (числами после знака равно в системе уравнений).
- вспомогательные определители, получаемые из главного заменой j-го столбца столбцом свободных членов (числами после знака равно в системе уравнений).
Чаще всего метод Крамера применяется для решения систем из 3 уравнений с 3 неизвестными, т.к. определители выше 4-го порядка вычислять трудоемко.
Дата добавления: 2018-04-05; просмотров: 355; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
