Взаємне положення двох площин
Дві площини у просторі можуть бути паралельними або перетинними. У першому випадку вони не мають спільних точок, у другому спільними точками цих площин є лінія їх перетину.
Дві площини паралельні (рис. 2.10) тоді, коли дві перетинні прямі однієї площини відповідно паралельні двом перетинним прямим другої площини.
Рисунок 2.10 – Взаємно паралельні площини
Якщо площини паралельні, то їх однойменні сліди також паралельні. Справедливим буде і обернене твердження.
Виходячи з того, що сліди площини є нульовими горизонталями, фронталями і профілями, справедливий також висновок: у паралельних площинах горизонталі, фронталі і профілі однієї площини паралельні відповідно до горизонталей, фронталей і профілей другої площини.
Дві перетинні площини (рис. 2.11) перетинаються по прямій лінії, для побудови якої досить визначити дві точки, що одночасно належать обом площинам, або одну таку точку і напрямок прямої перетину.
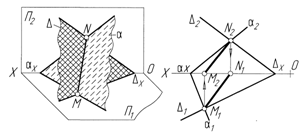
Рисунок 2.11 – Перетинні площини
Взаємно перпендикулярні площини – це окремий випадок двох площин, які перетинаються під прямим кутом. Дві площини взаємно перпендикулярні тоді, коли:
1) одна площина проведена через перпендикуляр до іншої;
2) одна перпендикулярна до будь-якої прямої, що лежить у другій площині.
Якщо йдеться про зображення на епюрі двох взаємно перпендикулярних площин, слід мати на увазі, що:
- однойменні сліди двічі проекційних площин взаємно перпендикулярні на тій площині проекцій, до якої обидві задані площини перпендикулярні (рис. 2.12-а);
· однойменні сліди проекційних площин взаємно перпендикулярні лише на тій площині проекцій, до якої обидві задані площини перпендикулярні, інші сліди – ні (рис. 2.12-б);
|
|
|
· якщо дві площини довільного положення на епюрі мають однойменні сліди перпендикулярні, то це не є ознакою перпендикулярності цих площин.
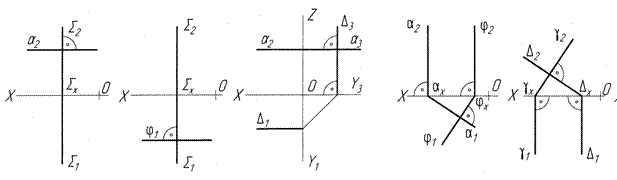
а) б)
Рисунок 2.12 – Взаємно перпендикулярні площини
Взаємне положення прямої і площини
Пряма і площина можуть займати одна відносно іншої такі положення: пряма належить площині; пряма паралельна площині; пряма перетинає площину.
Пряма паралельна до площини, коли вона паралельна будь-якій прямій, яка лежить у цій площині (рис. 2.13)
Пряма перетинає площину тоді, коли вона не належить площині і не паралельна їй, а перетинає її в певній точці.
Для побудови точки перетину прямої з площиною загального положення S треба виконати такі побудови (рис.2.14):
1) через задану пряму АВ провести допоміжну площину a (особливого положення);
2) побудувати лінію перетину MN заданої площини j з допоміжною a;
|
|
|
3) 
зробити висновок про положення прямих MN і АВ. Точка К є точкою перетину прямої АВ з площиною j.
 |
Пряму перпендикулярну до площини (рис. 2.15) слід розглядати як окремий випадок прямої, яка перетинає площину під прямим кутом.
Пряма перпендикулярна до площини, якщо вона перпендикулярна до двох перетинних прямих, які лежать у даній площині. На комплексному рисунку горизонтальна проекція перпендикуляра до площини є перпендикулярною до горизонтальної проекції горизонталі (до горизонтального сліду площини), а фронтальна – до фронтальної прекції фронталі (до фронтального сліду площини).
Дата добавления: 2018-04-05; просмотров: 87; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!