ПОЗИЦІЙНІ ТА МЕТРИЧНІ ЗАДАЧІ. СПОСОБИ
РОЗДІЛ 2. ОСНОВИ НАРИСНОЇ ГЕОМЕТРІЇ
Нарисна геометрія є граматикою інженерної графіки і вивчає теоретичні основи геометричного моделювання тривимірних об’єктів методом проекційних зображень.
Предметом нарисної геометрії є обґрунтування й викладання основних правил і методів побудови зображень просторових фігур на площині, а також способів розв’язування на зображеннях задач, що належать до цих фігур.
Прийняті позначення та символіка
Позначення геометричних фігур та їх проекцій, прийняті в курсі для запису алгоритмів розв’язування задач, відображення відношень між геометричними фігурами складені з позначень і символів, що використовуються в сучасній навчальній літературі з нарисної геометрії та креслення, а також в курсі геометрії для середньої школи.
Позначення геометричних фігур
1. Геометрична фігура - Ф..
2. Точки - А, В, С,... або 1, 2,3,....
3. Лінії (прямі та криві) - а, b, с,....
4. Поверхні - D, L, S,...
5. Кути - a, b, g,....
6. Осі проекцій:
Х – вісь абсцис;
Y – вісь ординат;
Z – вісь аплікат.
Символи, що позначають відношення між геометричними фігурами
|| - паралельність;
 - непаралельність;
- непаралельність;
^ - перпендикулярність;
∩ - перетин (а ∩ б - пряма а перетинається з прямою б);
 - мимобіжні прямі;
- мимобіжні прямі;
═ - результат дії;
≡ - тотожність, збіжність;
→ - відображення, випливає, якщо, ... то;
Є - належність.
ПРОЕКТУВАННЯ ЕЛЕМЕНТАРНИХ ГЕОМЕТРИЧНИХ ОБ’єктів
|
|
|
Побудова проекцій геометричних елементів ґрунтується на методі ортогонального паралельного проектування. В ортогональному проектуванні знаходять кілька проекцій оригіналу на взаємно перпендикулярні площини проекцій (рис. 2.1)


а) б)
Рисунок 2.1 – Ортогональна система двох (a) та трьох (б) площин проекцій
Площини проекцій: П1 – горизонтальна, П2 – фронтальна, П3 – профільна.
Дві площини проекцій ділять весь простір на чотири двогранні кути, які називають квадранти або чверті.
Три координатні площини проекцій ділять весь простір на вісім тригранних кутів, які називаються октантами.
Точка
Побудова точок в системі двох та трьох площин проекцій (рис. 2.2)


Рисунок 2.2 – Побудова епюра точки А (х; y; z).
Пряма лінія
Положення прямої у просторі характеризується положенням її відносно площин проекцій.
Пряма загального (довільного) положення не паралельна і не перпендикулярна до жодної з площин проекцій (рис. 2.3).

Рисунок 2.3 – Пряма довільного положення на комплексному рисунку
Прямі особливого положення:
горизонтальні – прямі паралельні до площини П1;
фронтальні – прямі паралельні до площини П2;
профільні – прямі паралельні до площини П3.
|
|
|
горизонтально-проекційні – прямі перпендикулярні до площини П1;
фронтально-проекційні – прямі перпендикулярні до площини П2;
профільно-проекційні – прямі перпендикулярні до площини П3.
Пряма може лежати на будь-якій площині проекцій чи розміщуватись на одній із трьох осей проекцій.
 |
Прямі лінії у просторі можуть перетинатися, бути паралельними і мимобіжними (рис. 2.4).
Рисунок 2.4 – Взаємне положення двох прямих
 |
Сліди прямої – це точки перетину прямої лінії з площинами проекцій (рис. 2.5)
Рисунок 2.5 – Знаходження горизонтального (М) та фронтального (N) слідів прямої
Площина
На епюрі площина задається проекціями трьох точок, що не лежать на одній прямій, проекціями прямої і точки, яка лежить поза нею, проекціями паралельних прямих, проекціями прямих, що перетинаються, плоскою фігурою та слідами (рис. 2.6).
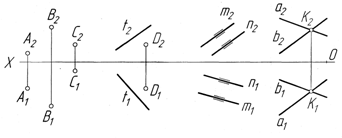

Рисунок 2.6 – Задання площини на комплексному рисунку
Слідом площини називають пряму лінію, по якій площина перетинається з площиною проекцій.
Положення площин у просторі характеризуються їх розміщенням відносно площин проекцій. У зв’язку з цим розрізняють площини довільного положення і особливі.
|
|
|
Площина довільного (або загального) положення – це площина не перпендикулярна і не паралельна жодній із площин проекцій (рис. 1.6).
Площина проекційна – це площина, яка перпендикулярна до однієї з трьох площин проекцій і не паралельна до двох інших.
Площина перпендикулярна до П1 – горизонтально-проекційна.
Площина перпендикулярна до П2 – фронтально-проекційна.
Площина перпендикулярна до П3 – профільно-проекційна.
Площиною рівня (двічі проекційною) називають площину, яка паралельна до однієї із площин проекцій і перпендикулярна до двох інших площин проекцій.
Площина паралельна до П1 – горизонтальна.
Площина паралельна до П2 – фронтальна.
Площина паралельна до П3 – профільна.
Точка належить площині, якщо вона лежить на прямій, яка належить цій площині.
Пряма належить площині, якщо вона:
- проходить через дві точки, які належать цій площині;
- проходить через точку, яка лежить у площині і проходить паралельно прямій, що лежить у цій площині.
Головні лінії площини: горизонталь, фронталь, профіль, лінія найбільшого нахилу.
Горизонталлю площини називають пряму, яка лежить у цій площині і паралельна до горизонтальної площини проекцій (рис. 2.7)
 |
Фронталлю площини називають пряму, яка лежить у площині і паралельна до фронтальної площини проекцій (рис. 1.8).
|
|
|
Рисунок 2.7 – Горизонталь площини Рисунок 2.8 – Фронталь площини
Профіль площини – це пряма, яка лежить у площині і паралельна до профільної площини проекцій.
Лінією найбільшого нахилу площини до площини проекцій називають пряму, яка лежить у площині і перпендикулярна до одного із слідів площини (рис. 1.9).

Рисунок 2.9 – Лінія найбільшого нахилу площини до П1
ПОЗИЦІЙНІ ТА МЕТРИЧНІ ЗАДАЧІ. СПОСОБИ
ПЕРЕТВОРЕННЯ ПРОЕКЦІЙ
Позиційними називають задачі, пов’язані з розв’язуванням на епюрі питань взаємного розміщення геометричних фігур або їх елементів. До них належать задачі на взаємну належність і на взаємний перетин.
Метричними називають задачі, пов’язані з визначенням на епюрі дійсних величин відстаней, кутів і плоских фігур.
Метричні і позиційні задачі на епюрі розв’язуються значно легше, якщо задані геометричні фігури займають особливе положення відносно площин проекцій. Тому, щоб спростити розв’язування задач, часто доцільно вдатися до такого перетворення заданих проекцій на епюрі, яке дає змогу перевести геометричні елементи із загального положення до особливого. У результаті цього нові проекції дають змогу просто і зручно виявити форму елементів, взаємне положення та дійсні величини прямих, плоских фігур, кутів тощо.
Перетворення епюра відображає зміну положення геометричних образів або площин проекцій у просторі. В основному використовуються два способи перетворення проекцій: заміна площин проекцій та обертання.
Дата добавления: 2018-04-05; просмотров: 395; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
