Показатели ряда динамики: абсолютные и относительные, базисные, цепные

ТЕМА 8РЯДЫ ДИНАМИКИ. ТРЕНД.

Вопросы.

1. Основные понятия рядов динамики.

2. Показатели ряда динамики: абсолютные и относительные, базисные, цепные.

3. Средние показатели динамики.

4. Выявление и характеристика основной тенденции развития.

Основные понятия рядов динамики.

Явления общественной жизни, изучаемые социально-экономической статистикой, находятся в непрерывном изменении и развитии. С течением времени – от месяца к месяцу, от года к году – изменяются численность населения и его состав, объем производимой продукции, уровень производительности труда и т. д., поэтому одной из важнейших задач статистики является изучение изменения общественных явлений во времени – процесса их развития, их динамики. Эту задачу статистика решает путем построения и анализа рядов динамики (временных рядов).

Ряд динамики (хронологический, динамический, временной ряд – синонимы) – это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Ряд включает два обязательных элемента: время и конкретное значение показателя (уровень ряда).

Каждое числовое значение показателя, по которому построен ряд, называется уровнем ряда.Каждый ряд динамики содержит указания о тех моментах либо периодах времени, к которым относятся уровни. Соответственно показатели ряда и сами ряды называются моментными и интервальными. (Пример – формы 1 и 2 бухгалтерского отчёта).

Итак, моментные ряды характеризуют явление на определённые моменты времениt, интервальные показывают итог развития явления или процесса за периоды времени - (t₀ – t₁), (t₁ – t₂), ….. (t_n_-1 – t_n).

В моментных рядах динамики есть промежутки (интервалы) времени между соседними в ряду датами, но величина того или иного конкретного уровня в общем случае не зависит от продолжительности этих периодов.

В интервальном ряду величина уровнязависит от продолжительности периода за который подводится итог. При прочих равных условиях уровень интервального ряда тем больше, чем больше длина интервала, к которому этот уровень относится.

Иногда путем последовательного сложения уровней интервального ряда за примыкающие друг к другу интервалы времени строится ряд нарастающих (кумулятивных) итогов, в котором каждый уровень представляет собой итог не только за данный период, но и за предшествующие периоды. (Форма 2).

В моментном динамическом ряду последующие уровни обычно являются результатом развития предыдущих, поэтому суммирование уровней моментного ряда динамики само по себе не имеет смысла, так как получающиеся при этом итоги лишены самостоятельной экономической значимости. (Форма 1).

Выше говорилось о рядах динамики абсолютных величин, являющихся исходными, первичными. Наряду с ними могут быть построены ряды динамики, уровни которых являются относительными и средними величинами. Они также могут быть либо моментными, либо интервальными. В интервальных рядах динамики относительных и средних величин непосредственное суммирование уровней само по себе лишено смысла, так как относительные и средние величины являются производными и исчисляются путем деления других величин.

При построении и анализе ряда динамики надо соблюдать требование сопоставимости уровней ряда. Сопоставимость уровней ряда динамики означает, что за период наблюдения не произошло нарушающих её изменений – изменений территории, методики измерения, наблюдаемой совокупности и т.п.

Основные случаи несопоставимости рядов динамики:

1) территориальные изменения объекта исследования, к которому относится изучаемый показатель;

2) разновеликие интервалы времени, к которым относится показатель;

3) изменение даты учета;

4) изменение методологии учета или расчета показателя;

5) изменение цен;

6) изменение единиц измерения.

Ряды делятся на равно и не равностоящие.

Равностоящие – измерения происходят через равные промежутки времени или за равные интервалы, не равностоящие – измерения производятся через неравные промежутки времени или за неравные интервалы.

Полный ряд динамики – нет разрывов между учётными датами или интервалами измерений.

Показатели ряда динамики: абсолютные и относительные, базисные, цепные.

Задачи, возникающие при изучении динамических рядов:

1) характеристика интенсивности отдельных изменений в уровнях рода от периода к периоду или от даты к дате;

2) определение средних показателей временного ряда за тот или иной период;

3) выявление основных закономерностей динамики исследуемого явления на отдельных этапах и в целом за рассматриваемый период;

4) выявление факторов, обусловливающих изменение изучаемого объекта во времени;

5) прогноз развития явления на будущее.

Эти задачи решаются с помощью показателей изменения уровней ряда динамики.

Способы сопоставления уровней ряда:

1) каждый уровень динамического ряда сравнивается с одним и тем же предшествующим уровнем, где базисный уровень - начальный уровень динамического ряда или уровень, с которого начинается какой-то новый этап развития - это сравнение с постоянной базой. Полученные при этом показатели называются базисными;

2) каждый уровень динамического ряда сравнивается с непосредственно ему предшествующим - это сравнение с переменной базой. Полученные при этом показатели называются цепными.

Обычными показателями, которые используются ванализерядов динамики, являются:

- абсолютный прирост, а также

- абсолютная скорость ростаи

- абсолютное ускорение роста,

- темпы роста и прироста,

- абсолютное значение (содержание) одного процента прироста.

Абсолютный прирост показывает, на сколько единиц увеличился (или уменьшился) уровень по сравнению с базисным уровнем, т. е. за тот или иной промежуток (период) времени. Абсолютный прирост равен:

Δ_б_i =y_i - y₀, - базисный прирост (44)

Абсолютная скорость роста- это абсолютный прирост с переменной базой за единицу времени (цепной прирост):

Δ_ц_i =y_i - y_i-1; (44-1)

где у_i– уровень i-го года;

y_i-1 – уровень предшествующего года;

y₀ – уровень базисного года.

Абсолютный прирост и абсолютная скорость роста (цепной прирост) связаны между собой: сумма последовательных цепных приростов (абсолютной скорости роста) равна соответствующему базисному приросту, т. е. общему приросту за весь период:

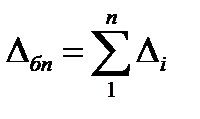(45)

Абсолютное ускорение роста - разность между абсолютным приростом за данный период и абсолютным приростом за предыдущий период одинаковой длительности:

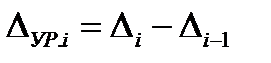(46)

Приведённые показатели могут иметь положительные и отрицательные значения.

Более полную характеристику роста можно получить только тогда, когда абсолютные величины дополняются относительными. Относительными показателями динамики являются темпы роста и темпы прироста, характеризующие интенсивность процесса роста.

Темп роста (Т_р) – статистический показатель, который отражает интенсивность изменения уровней ряда динамики и показывает, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения – какую часть базисного уровня составляет сравниваемый уровень; измеряется отношением текущего уровня к предыдущему или базисному и измеряется в коэффициентах, процентах и т.д.:

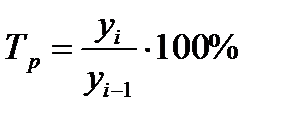- цепной темп прироста (47)

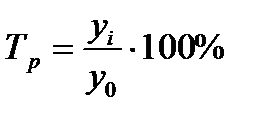- базисный темп прироста (48)

Между цепными и базисными темпами роста, выраженными в форме коэффициентов, существует определенная взаимосвязь: произведение последовательных цепных темпов роста равно базисному темпу роста за весь соответствующий период.

Темп прироста (Т_ПР) характеризует относительную величину прироста, т. е. представляет собой отношение абсолютного приростак уровню ряда, относительно которого определён прирост:

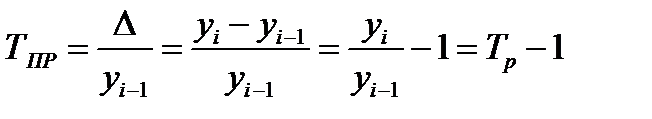- цепной темп прироста (49)

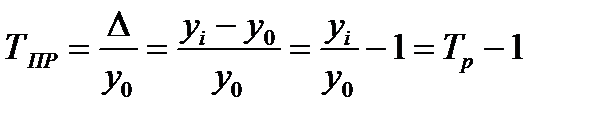- базисный темп прироста (50)

Абсолютные приросты и темпы роста для любых рядов динамики характеризуют тот или иной промежуток (интервал) времени. Эти соотношения справедливы и при исчислении темпов роста и прироста в процентах.

При анализе темпов развития никогда не следует упускать из виду, какие абсолютные величины – уровни и абсолютные приросты – скрываются за темпами роста и прироста. Нужно, в частности, иметь в виду, что при снижении (замедлении) темпов роста и прироста абсолютный прирост может возрастать.

В связи с этим важно изучать еще один показатель динамики – абсолютное значение (содержание) 1 % прироста, который определяется как результат деления абсолютного прироста на соответствующий темп прироста, %:

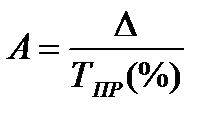(51)

Эта величина показывает, сколько в абсолютном выражении дает каждый процент прироста.

Иногда уровни явления за одни годы несопоставимы с уровнями за другие годы из-за территориальных, ведомственных и иных изменений (изменения методологии учета и исчисления показателей и т. п.). Чтобы обеспечить сопоставимость и получить пригодный для анализа временной ряд, нужно произвести прямой пересчет уровней, несопоставимых с другими. Однако иногда нет необходимых для этого данных. В таких случаях можно использовать особый прием, называемый смыканием рядов динамики.

Пусть, например, произошло изменение границ территории, по которой изучалась динамика развития какого-то явления в i-м году. Тогда данные, полученные до этого года, окажутся несопоставимы с данными за последующие годы. Чтобы сомкнуть эти ряды и получить возможность анализа динамики ряда за весь период, примем в каждом из них за базу сравнения уровень i-го года, за который есть статистические данные, как в прежних, так и в новых границах территории.

В этом случае показатели до этого года включительно строятся для исходных территориальных границ, а затем, начиная с этого же года, строятся показатели ряда для новых границ (Пример).

ПРИМЕР:ВВП области (края) в старых и новых границах.

Показатели		Старые границы			Новые границы
Показатели		2007	2008	2009	2010	2011	2012
ВВП, млн.р.	стар. гран.	45000	47000	46000
ВВП, млн.р.	нов. гран.	51851,3	54153,5= 53000/97,87%	53000	55200	57000	58900
Абс. прирост: фактич. оценочн.в новых гран.			2000 2302,2	-1000 -1153,5	2200	1800	1900
Темп прироста, %			4,44%	-2,13%	4,15%	3,26%	3,33
Темп роста,%			104,44% = 47000/45000	97,87%= 46000/47000	104,15%	103,26%	103,33%
Абс. значение 1 % прироста, млн.р.: фактический оценочн.в новых гран.			450,45 518,5	-469,48 541,55	530,12	552,15	736,38

Алгоритм:

- рассчитываются темпы роста;

- определяются по темпам роста оценочные уровни в старых границах;

и т.д.

Эти два ряда с одинаковой базой сравнения можно затем заменить одним сомкнутым рядом динамики. По данным сомкнутого ряда можно вычислить темпы роста по сравнению с любым годом, можно рассчитать и абсолютные уровни за весь период в новых границах. Тем не менее, надо иметь в виду, что результаты, полученные путем смыкания рядов динамики, содержат в себе некоторую погрешность.

Графически динамика явлений наиболее часто изображается в виде столбиковых и линейных диаграмм. Применяются и другие формы диаграмм: фигурные, квадратные, секторные и т. п. Аналитические графики обычно строятся в виде линейных диаграмм.

При сравнении рядов динамики с разными показателями или с разными значениями уровней, например, при сравнении динамики ВВП и динамики промышленного производства осуществляется приведение рядов динамики к одному основанию. Это означает переход к относительным показателям, при котором значения базовых уровней на единый момент (или за единый интервал) принимается за единицу (100%), и последующие уровни рассчитываются по отношению к этой базе.

Средние показатели динамики

С течением времени изменяются не только уровни явлений, но и показатели их динамики – абсолютные приросты и темпы развития. Поэтому для обобщающей характеристики развития, для выявления и измерения типичных основных тенденций и закономерностей и решения других задач анализа используются средние показатели временного ряда:

- средние уровни,

- средние абсолютные приросты и

- средние темпы динамики (роста).

К расчету средних уровней ряда динамики часто приходится прибегать уже при построении временного ряда – для обеспечения сопоставимости числителя и знаменателя при расчете средних и относительных величин. Допустим, например, требуется построить ряд динамики производства ВВП на единицу населения в Российской Федерации. Для этого за анализируемые годы необходимо объём ВВП в данном году (интервальный показатель) разделить на численность населения в том же году (моментный показатель, непрерывно изменяющийся на протяжении года). Очевидно, что численность населения на любой отдельный момент времени в общем случае несопоставима с объемом ВВПза весь год. Для сопоставимости необходимо численность населения отнести ко всему году, а это можно сделать, толькорассчитав среднюю численность населения за год.

Часто приходится прибегать к средним показателям динамики и потому, что уровни многих явлений сильно колеблются от периода к периоду, например от квартала к кварталу, то повышаясь, то понижаясь. Особенно это относится ко многим показателям сельского хозяйства, где год на год и квартал на квартал не приходятся. При анализе развития сельского хозяйства,поэтому,чаще оперируют не годовыми показателями, а более типичными и устойчивыми среднегодовыми показателями за несколько лет.

При вычислении средних показателей динамики необходимо иметь в виду, что к этим средним показателям полностью относятся общие положения теории средних величин. Это означает, прежде всего, что динамическая средняя будет типичной, если она характеризует период с однородными, более или менее стабильными условиями развития явления. Выделение таких периодов – этапов развития – в определенном отношении аналогично группировке. Если же динамическая средняя величина исчислена за период, в течение которого условия развития явления существенно менялись, то такой средней величиной нужно пользоваться с большой осторожностью, дополняя ее средними величинами за отдельные этапы.

Средние показатели динамики должны также удовлетворять логико-математическому требованию, согласно которому при замене средней величиной тех фактических величин, из которых получена средняя, не должна изменяться величина определяющего показателя, т. е. некоторого обобщающего показателя, связанного с усредняемым показателем. Метод расчета среднего уровня ряда динамики зависит прежде всего от характера показателя, лежащего в основе ряда, т. е. от вида временного ряда.

Наиболее просто вычисляется средний уровень интервального ряда динамики абсолютных величин с равностоящими уровнями. Расчет производится по формуле простой средней арифметической:

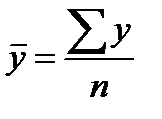(52)

где n – число фактических уровней за последовательные равные отрезки времени;

y – уровни ряда.

Пример. Среднеквартальный объем товарной продукции = сумма по кварталам/4.

Для интервального ряда с не равностоящими уровнями:

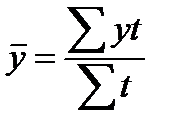(53)

где t–отрезки времени, за которые измерены уровни ряда - y.

Сложнее обстоит дело с вычислением среднего уровня моментного ряда динамики абсолютных величин. Моментный показатель может изменяться почти непрерывно, поэтому, чем более подробны и исчерпывающи данные о его изменении, тем более точно можно вычислить средний уровень. Более того, сам метод расчета зависит от того, насколько подробны имеющиеся данные. Здесь возможны различные случаи.

При наличии исчерпывающих данных об изменении моментного показателяего средний уровень вычисляется по формуле средней арифметической взвешенной для интервального ряда с разностоящими уровнями:

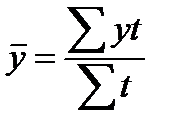(54)

где t – число периодов времени, в течение которых уровень не изменялся.

Исчерпывающие данные – это наличие данных за все возможные моменты изменения показателя. Например, при расчёте средней численности персонала за месяц исчерпывающие данные - это данные о численности персонала на каждый день месяца. (Если имеются данные только на начало и конец месяца, то для расчёта средней численности персонала будет применена средняя хронологическая).

(Соотнести с формулой 56)

Если исчерпывающие данные отсутствуют, а интервалы между учётными датами равны, или примерно равны между собой (например, когда известны уровни на начало каждого месяца или квартала, года), то есть ряд равностоящий, то расчёт среднего уровня ряда можно провести по формуле средней хронологической:

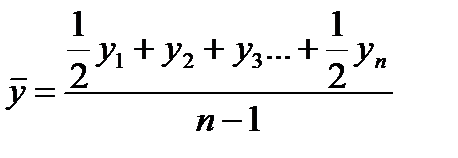(55)

См. также пример перед формулой.

Для моментного ряда с не равностоящими уровнями расчет среднего уровня ряда производится по формуле:

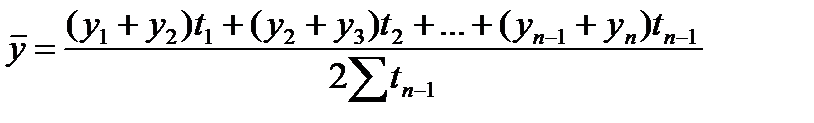(56)

Выше шла речь о среднем уровне рядов динамики абсолютных величин. Для рядов динамики средних и относительных величин средний уровень нужно вычислять исходя из содержания и смысла этих средних и относительных показателей.

Средний абсолютный прирост показывает, на сколько единиц увеличивался или уменьшался уровень по сравнению с предыдущим периодом в среднем за единицу времени (в среднем ежемесячно, ежегодно и т. д.). Средний абсолютный прирост характеризует среднюю абсолютную скорость роста (или снижения) уровня и всегда является интервальным показателем. Он вычисляется путем деления общего прироста за весь период на длину этого периода в тех или иных единицах времени:

расчет среднего абсолютного цепного прироста:

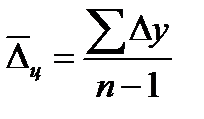(57)

расчет среднего абсолютного базисного прироста:

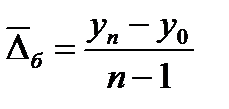(58)

(они равны при прочих равных условиях)

где 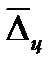и 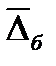-цепныеи базисные абсолютные приросты; n – число уровней; y₀ – уровень базисного периода.

Средний темп роста за nпериодов, то есть средний цепной темп роста, определяется по формуле средней геометрической:

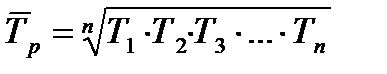(59)

где n – число уровней ряда динамики;

Т₁, Т₂, …Т_n– цепные темпы роста.

Средний темп роста, выраженный в форме коэффициента, показывает, во сколько раз увеличивается уровень по сравнению с предыдущим периодом в среднем за период измерения (в среднем ежегодно, ежемесячно и т. п.).

Для средних темпов роста и прироста сохраняет силу та же взаимосвязь, которая имеет место между обычными темпами роста и прироста:

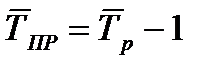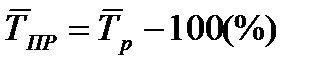или (60)

Средний темп прироста (или снижения), выраженный в процентах, показывает, на сколько процентов увеличивался (или снижался) уровень по сравнению с предыдущим периодом в среднем за единицу времени (в среднем ежегодно, ежемесячно и т. п.). Средний темп прироста характеризует среднюю интенсивность роста, т. е. среднюю относительную скорость изменения уровня.

Дата добавления: 2018-04-05; просмотров: 4541; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!