Метод подведения под знак дифференциала (устная замена переменной)
Nbsp; Министерство образования и науки Российской Федерации Кубанский Государственный Технологический университет Кафедра прикладной математики МАТЕМАТИКА II часть Методические указания и контрольные задания для студентов МИППС первого курса технических специальностей заочной формы обучения Краснодар 2005 Составители: канд. физ-мат. наук, доц. С. Н. Горшкова; канд. техн. наук, доц. Л. М. Данович; канд. техн. наук, доц. А. С. Арутюнян; ст. преп. И.И.Петрушина; ст. преп. Т. А. Карачанская УДК 517 Математика. Методические указания и контрольные задания для студентов МИППС первого курса технических специальностей заочной формы обучения, II часть/ Сост.: С. Н. Горшкова; Л. М. Данович; И.И.Петрушина; Т. А. Карачанская; А. С. Арутюнян; Кубан. гос. технол. ун-т. Каф. прикладной математики. – Краснодар: Изд. КубГТУ, 2005. – 42 с. Приведён теоретический материал, даны основные формулы, разобрано решение типовых задач, даны контрольные задания Переиздание Печатается по решению Редакционно-издательского совета Кубанского государственного технологического университета. Рецензенты: канд. физ-мат. наук, доц. И.В.Терещенко канд. техн. наук В.И.Алёшин ПРОГРАММА КУРСА МАТЕМАТИКИ Тема 1. Первообразная. Неопределенный интеграл, его свойства. Таблица основных интегралов. Непосредственное интегрирование. Интегрирование по частям и подстановкой. Тема 2. Определенный интеграл, его свойства. Формула Ньютона-Лейбница. Интегрирование по частям и замена переменной. Приложения определенного интеграла . Тема 3. Несобственные интегралы с бесконечными пределами и от разрывных функций. Тема 4. Дифференциальные уравнения первого порядка. Уравнения с разделяющимися переменными, однородные, линейные. Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами. Уравнения с правой частью специального вида. Тема 5. Системы дифференциальных уравнений. Метод исключения. Тема 6. Числовые ряды. Сходимость, сумма ряда. Знакоположительные ряды. Признаки сходимости. Знакопеременные ряды. Признак Лейбница. Степенные ряды. Теорема Абеля. Приложения степенных рядов. Тема 7. Теория вероятностей. Случайные события, операции над событиями. Классическое определение вероятности. Вероятность суммы и произведения событий. Формула полной вероятности. Формула Бернулли. Случайная величина. Интегральная и дифференциальная функции. Математическое ожидание, дисперсия, их свойства. Нормальное распределение. Основная литература 1.Пискунов Н. С. Дифференциальное и интегральное исчисления. - М.: Наука 1978 и др. 2.Шнейдер В. Е. Краткий курс высшей математики./Слуцкий И. А., Шумов А. С. - М.: Высшая школа, 1972 3.Чистяков В. П. Курс теории вероятностей.- М.: Наука, 1982 4.Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 1979 5.Данко П. Е. и др.Высшая математика в упражнениях и задачах./ Данко П.Е., Попов А. Г., Кожевникова Т. Я. - М.: Высшая школа, 1980, II ч.
|
|
|
|
|
|
Интегральное исчисление
1.1 Первообразная, неопределенный интеграл
Определение. Функция F(x) называется первообразной функции f(x) на множестве X, если 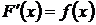 для всех
для всех 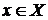 .
.
Выражение F(x)+C представляет собой семейство всех первообразных функции f(x). (C=const).
Определение. Если F(x) – одна из первообразных функции f(x), то выражение F(x)+C называется неопределенным интегралом.
Обозначается 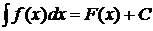 .
.
Простейшие свойства.
1) 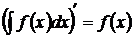
2) 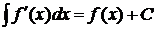
3) 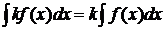
4) 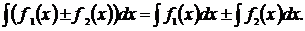
Таблица основных интегралов
1) 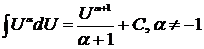 . .
| 10) 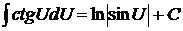 . .
|
2) 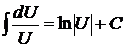 . .
| 11) 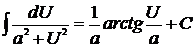 . .
|
3) 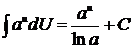 . .
| 12) 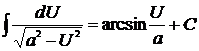 . .
|
4) 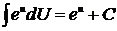 . .
| 13) 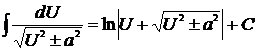 . .
|
5) 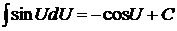 . .
| 14) 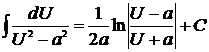 . .
|
6) 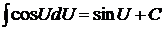 . .
| 15) 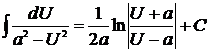 . .
|
7) 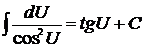 . .
| 16) 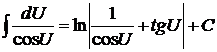 . .
|
8) 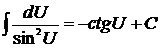 . .
| 17) 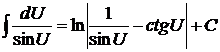 . .
|
9)  . .
|
В частности:
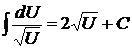 ;
; 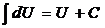 ;
; 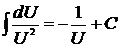 .
.
Из определения и свойств неопределенного интеграла следует, что дифференцирование и интегрирование являются взаимно обратными действиями: производная правой части в каждой формуле равна подынтегральной функции. Проверим, например, формулу 2.
|
|
|
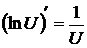
Примеры:
1) 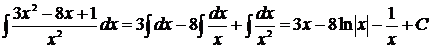 ;
;
2) 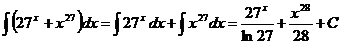 .
.
Методы интегрирования
Метод подведения под знак дифференциала (устная замена переменной)
Если относительно данной переменной интеграл не является табличным, то в некоторых случаях его можно привести к табличному относительно новой переменной с помощью подведения под знак дифференциала нужной функции.
При этом удобно пользоваться следующими формулами, которые получаются из формул дифференцирования при прочтении их в обратном порядке:
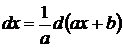
| 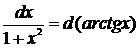
|
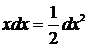
| 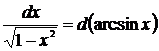
|
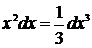
| 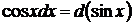
|
| … | 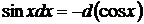
|
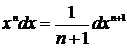 , n≠-1 , n≠-1
| 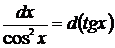
|
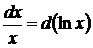
| 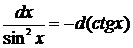
|
Примеры (см. задание 1а)
1) 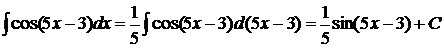 ;
;
2) 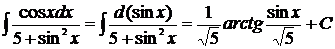
3) 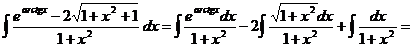
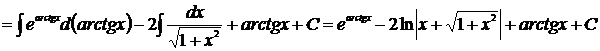
Дата добавления: 2018-04-05; просмотров: 215; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
