Тема: Элементы теории ошибок измерений

Классификация ошибок измерений.

Измерения в геодезии рассматриваются с двух точек зрения: количественной, выражающей числовое значение измеренной величины, и качественной, характеризующей ее точность. Из практики известно, что даже при самой тщательной и аккуратной работе многократные (повторные) измерения не дают одинаковых результатов. Это указывает на то, что получаемые результаты не являются точным значением измеряемой величины, а несколько отклоняются от него. Значение отклонения характеризует точность измерений.

При геодезических измерениях неизбежны ошибки. Эти ошибки бывают грубые, систематические и случайные.

К грубым ошибкам относятся просчеты в измерениях по причине невнимательности наблюдателя или неисправности прибора, и они полностью должны быть исключены. Это достигается путем повторного измерения.

Систематические ошибки происходят от неизвестного источника, имеют определенный знак и величину и их можно учесть при измерениях и вычислениях.

Случайные ошибки обусловлены разными причинами и полностью исключить их из измерений нельзя. Поэтому возникают две задачи: как из результатов измерений получить наиболее точную величину и как оценить точность полученных результатов измерений. Эти задачи решаются с помощью теории ошибок измерений.

В основу теории ошибок положены следующие свойства случайных ошибок:

 

1. Малые ошибки встречаются чаще, а большие реже.

2. Ошибки не превышают известного предела.

3. Положительные и отрицательные ошибки, одинаковые по абсолютной величине, 

одинаково часто встречаются.

4. Сумма ошибок, деленная на число измерений, стремится к нулю при большом числе

измерений.

 

По источнику происхождения различают ошибки приборов, внешние и личные.

Ошибки приборов обусловлены их несовершенством, например погрешность угла, измеренного теодолитом, неточным приведением в вертикальное положение оси его вращения.

Внешние ошибки происходят из-за влияния внешней среды, в которой протекают измерения, например погрешность в отсчете по нивелирной рейке из-за изменения температуры воздуха на пути светового луча (рефракция) или нагрева нивелира

солнечными лучами.

Личные ошибки связаны с особенностями наблюдателя, например, разные наблюдатели по-разному наводят зрительную трубу на визирную цель. Так как грубые погрешности должны быть исключены из результатов измерений, а систематические исключены или ослаблены до минимально допустимого предела, то проектирование измерений с необходимой точностью и оценку результатов выполненных измерений производят, основываясь на свойствах случайных погрешностей.

,

Арифметическая средина.

  Если одна величина измерена n раз и получены результаты: l₁, l_2, l_3, l_4, l_5, l_6,….., l_n,

то

 

 

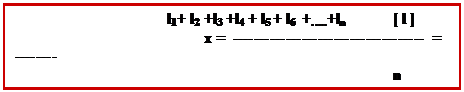
Величина x  называется арифметической срединойили вероятнейшим значением измеренной величины. Разности между каждым измерением и арифметической срединой называют вероятнейшими ошибками измерений:

 

l₁ – x = v₁

l₂ – x = v₂

l₃ – x = v₃

                                                                 . . . . . . . .

l_n – x = v_n

 

 

Или в общем виде получим:

 

                                                                  [ l ] – nx = [v]

Тогда [v] = 0.

 

Средняя квадратическая ошибка.

 

  Точность результатов измерений оценивается средней квадратической ошибкой. Средняя квадратическая ошибка одного измерения вычисляется по формуле:

 

                                                  [v²]

m   = √ n - 1

где [v²] – сумма квадратов вероятнейших ошибок; n – число измерений.

  Средняя квадратическая ошибка арифметической середины вычисляется по формуле:

 

 

                         m             [v²]       

                M = ----------- = √ --------------

                              √n            n ( n – 1 )

  Предельная ошибка не должна превышать утроенной средней квадратической ошибки, т.е.

 

                                     ε = 3m.

Иногда о точности измерений судят не по абсолютной величине средней квадратической или предельной погрешности, а по величине относительной ошибки. Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной ве-

личины. Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух-трех значащих цифр с нулями. Например, относительная средняя квадратическая погрешность измерения линии длиной

 l = 110 м, при m = 2 см равна m/l = 1/5500.

 

---

Дата добавления: 2018-04-05; просмотров: 859; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!