Скалярное, векторное и смешанное произведения векторов
1о. Проекции вектора на ось
Пусть в пространстве задана некоторая прямая l и вектор 
.
Определение 1.Осью l будем называть прямую, на которой задано направление. Направление оси задается вектором 
(направляющий вектор оси).
Рис.2.1. Проекция точки А на ось l.
Пусть 
– точка, не принадлежащая l. Проведем через точку плоскость p^l. Получим точку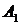 
, которая называется проекцией (ортогональной проекцией) точки на ось l. Обозначение: 
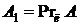(см. рис.2.1).
Если наряду с точкой взять точку B, то можно построить 
.
Определение 2.Так построенный вектор 
называется векторной проекцией вектора 
на ось l. Обозначают: 
.
Иногда говорят, что есть компонента вектора на оси l.
Вектора и 
– коллинеарны Þ 
R: 
.
Определение 3.Такое число 
называется скалярной проекцией (проекцией) вектора на ось l с масштабным вектором . В этом случае рассматривается как единичный вектор. Пишут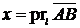 
или 
.
Таким образом 
.
Легко видеть, что 
Û ^ .
Свойства проекции.
10. Проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и осью:
.
 |
Рис.2.2. 
- проекция вектора на ось l. а) 
, б)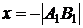 
Действительно, пусть 
.
Если 
(см. рис. 2.2а), то 
, поэтому
.
Если 
(см. рис. 2.2б), то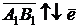 
, и
.
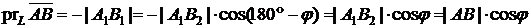20. При умножении вектора на число его проекция на ось также умножается на это число: 
.
Действительно, если 
, то угол между векторами 
и равен углу между и , то есть 
l и 
.
Если 
, то 
30. Проекция суммы векторов на ось равна сумме проекций слагаемых:
.
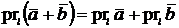Справедливость этого утверждения следует из рис.9. В случае а) 
, б)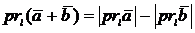 
Дата добавления: 2018-04-05; просмотров: 281; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!