Свойства умножения вектора на число
Геометрические векторы 1о. Направленные отрезки. Векторы и операции над векторами. Рассмотрим в пространстве две точки А и В. Они определяют отрезок АВ. Определение 1.Отрезок АВ называется направленным, если его концы А и В упорядочены; если при этом первой является точка А, а второй – точка В, то А – начало отрезка, а В – его конец. Направленный отрезок обозначается AB (а также или ). На чертеже направленный отрезок снабжен стрелкой на конце (см. рис.1.1). Определение 2.Длиной направленного отрезка называется длина отрезка АВ. Рис.1.1. Направленный отрезок АВ. Определение 3.Направленные отрезки и называются сонаправленными (обозначается ), если они лежат на параллельных прямых и направлены в одну сторону. Направленные отрезки и называют противоположно направленными (пишут ), если они лежат на параллельных прямых и направлены в разные стороны. Направленные отрезки и называются противоположными. Каждую точку А пространства можно рассматривать как направленный отрезок с совпадающим началом и концом. Этот отрезок обозначается и называется нулевым направленным отрезком. Его длина считается равной нулю, а направление не определено. Определение 4.Два направленных отрезка и считаются эквивалентными, если они сонаправлены и имеют равные длины. (Обозначают ). Эквивалентность является отношением эквивалентности в множестве всех направленных отрезков, т.к. из определения эквивалентности следует: 1) отрезок эквивалентен сам себе; 2) если эквивалентен , то эквивалентен ; 3) если эквивалентен и эквивалентен , то эквивалентен . Так как эквивалентность направленных отрезков является отношением эквивалентности, то множество всех направленных отрезков пространства разбивается на непересекающиеся классы – классы эквивалентности. Классы эквивалентности образуют фактор-множество множества всех направленных отрезков пространства. Определение 5.Множество всех эквивалентных направленных отрезков называется вектором (или свободным вектором). Направление эквивалентных направленных отрезков называется направлением вектора, а их длина – длиной вектора. Таким образом, любой направленный отрезок однозначно определяет вектор, а вектор – это класс эквивалентных направленных отрезков. Поэтому часто пишут вектор , . Определение 6.Вектор a такой, что , называется единичным вектором или ортом. Множество нулевых отрезков называется нулевым вектором ; его длина равна нулю, а направление не определено. Определение 7.Два ненулевых вектора, направления которых совпадают или противоположны, называются коллинеарными. Обозначают . Нулевой вектор считается коллинеарным любому вектору. Очевидно, что прямые, на которых лежат представители классов коллинеарных векторов, параллельны. Определение 8.Три и более векторов называются компланарными, если они параллельны некоторой плоскости. Для определенности любую тройку векторов, содержащую нулевой вектор, считают компланарной. Пусть даны два вектора a и b. Из произвольной точки O пространства отложим и . Тогда есть направленный отрезок и значит, определяет вектор. Покажем, что введенная операция сложения векторов корректно определена, т.е. вектор не зависит от выбора точки O. Для этого выберем другую точку . Пусть , . Тогда – параллелограмм; аналогично, – параллелограмм – параллелограмм , то есть они определяют один и тот же вектор. Определение 9.Вектор называется суммой векторов и . Пишут: . Способ сложения векторов, изложенный выше, называется правилом треугольника. Можно также использовать правило параллелограмма.
|
|
|
|
|
|
Свойства сложения векторов.
1.  .
.
2.  .
.
3.  , так как
, так как  .
.
4. Для каждого вектора 
 вектор, называемый вектором, противоположным
вектор, называемый вектором, противоположным  , такой, что
, такой, что  .
.
Доказательство свойств может быть проиллюстрировано рис.1.2.
|
|
|
 а) б)
а) б)
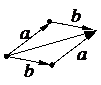 |
Рис.1.2. Свойства сложения векторов: а) коммутативность, б) ассоциативность
Если  , то через
, то через  обозначим
обозначим  . Тогда
. Тогда  .
.
Определение 10.Произведением вектора  на число
на число 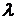
 R,
R,  называется вектор
называется вектор  , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1) векторы  и
и  сонаправлены, если
сонаправлены, если  и противоположно направлены, если
и противоположно направлены, если  ;
;
2) 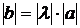 .
.
Произведение вектора на число 0 есть нулевой вектор. Пишут  .
.
Свойства умножения вектора на число.
1)  и
и 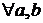

 .
.
2)  и
и  вектора
вектора 

 .
.
3)  и
и  вектора
вектора 

 .
.
4)  вектора
вектора 

 .
.
Доказательство 1). Пусть для простоты  и будем использовать правило параллелограмма для сложения векторов. Если вместо
и будем использовать правило параллелограмма для сложения векторов. Если вместо  и
и  взять
взять  и
и  , то получим подобный параллелограмм и его диагональ соответственно равна
, то получим подобный параллелограмм и его диагональ соответственно равна 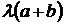 (см. рис.1.3).
(см. рис.1.3).

Рис.1.3. Иллюстрация свойства сложения векторов 
Доказательство 2)–4). Очевидно с учетом того, что при этом получаются коллинеарные вектора.
 |
Замечание. Можно определить операцию вычитания векторов по формуле
 (см. рис.1.4)
(см. рис.1.4)
Рис. 1.4. Вычитание векторов
2о. Линейно зависимые и линейно независимые системы векторов
Определение 11.Линейной комбинацией векторов  с коэффициентами
с коэффициентами  R называется выражение вида:
R называется выражение вида:  .
.
|
|
|
Определение 12.Вектора  называются линейно зависимыми, если
называются линейно зависимыми, если  R, из которых хотя бы одно отлично от нуля, и линейная комбинация
R, из которых хотя бы одно отлично от нуля, и линейная комбинация  с этими
с этими  является нулевым вектором, т.е.
является нулевым вектором, т.е.  .
.
Определение 13.Вектора  , не являющиеся линейно зависимыми, называются линейно независимыми. Другими словами,
, не являющиеся линейно зависимыми, называются линейно независимыми. Другими словами,  называются линейно независимыми, если их линейная комбинация является нулевым элементом лишь при условии, что
называются линейно независимыми, если их линейная комбинация является нулевым элементом лишь при условии, что 
Теорема 1.
1) Для того, чтобы элементы  были линейно зависимы, необходимо и достаточно, чтобы один из этих элементов был линейной комбинацией остальных.
были линейно зависимы, необходимо и достаточно, чтобы один из этих элементов был линейной комбинацией остальных.
2) Если среди  один элемент нулевой, то они линейно зависимы.
один элемент нулевой, то они линейно зависимы.
3) Если часть элементов множества  линейно зависима, то и все элементы линейно зависимы.
линейно зависима, то и все элементы линейно зависимы.
Доказательство.
1. 
 Пусть векторы
Пусть векторы  – линейно зависимы, т.е.
– линейно зависимы, т.е.  и, например,
и, например, 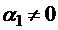 . Тогда
. Тогда  и
и 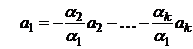 , т.е.
, т.е.  является линейной комбинацией
является линейной комбинацией  .
.
 Пусть
Пусть  . Тогда
. Тогда  , где
, где  , т.е.
, т.е.  – линейно зависимы.
– линейно зависимы.
2. Если 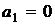

 и
и  – любое, например,
– любое, например, 

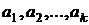 - линейно зависимы.
- линейно зависимы.
3. Если  – линейно зависимы, то
– линейно зависимы, то  одновременно неравные нулю, так что
одновременно неравные нулю, так что 

 и хотя бы одно из
и хотя бы одно из  отлично от нуля
отлично от нуля 
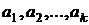 – линейно зависимы. ч.т.д.
– линейно зависимы. ч.т.д.
Теорема 2. Два вектора коллинеарны тогда и только тогда, когда они линейно зависимы.
Доказательство. Если один из векторов нулевой, то очевидно. Поэтому далее предполагаем, что оба вектора ненулевые.
 Пусть
Пусть  и
и  – коллинеарны. Отложим их от одной точки. Пусть
– коллинеарны. Отложим их от одной точки. Пусть  . Тогда если
. Тогда если  , то
, то  , если
, если  , то
, то  . В обоих случаях
. В обоих случаях  и
и  – линейно зависимы.
– линейно зависимы.
 Пусть
Пусть  и
и  – линейно зависимы, т.е.
– линейно зависимы, т.е.  , где
, где  не равно 0. Тогда, если
не равно 0. Тогда, если  ,
, 
 по определению10
по определению10 
 и
и  коллинеарны.∎
коллинеарны.∎
Следствие 1. Если  и
и  – коллинеарны и
– коллинеарны и 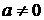 , то
, то  R:
R:  .
.
Доказательство.  R:
R:  . Если
. Если 

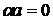

 . Т.о.
. Т.о. 

 и
и  .
.
Теорема 3. Три вектора компланарны тогда и только тогда, когда они линейно зависимы.
Доказательство. Будем предполагать, что никакие два вектора из трех не коллинеарны, так как иначе утверждение очевидно в силу свойства линейно зависимых векторов.
 Пусть вектора
Пусть вектора  компланарны. Перенесем их в точку O, проведем через конец вектора c прямые, параллельные векторам
компланарны. Перенесем их в точку O, проведем через конец вектора c прямые, параллельные векторам  и
и  и рассмотрим параллелограмм
и рассмотрим параллелограмм  .(см. рис. 1.5) Векторы
.(см. рис. 1.5) Векторы  и
и  ,
,  и
и  – коллинеарны
– коллинеарны 
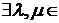 R:
R:  ,
,  . Но
. Но 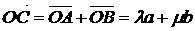

 ,
,  ,
,  – линейно зависимы.
– линейно зависимы.
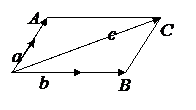
Рис.1.5. Иллюстрация доказательства теоремы 3.
 Пусть
Пусть  ,
,  ,
,  – линейно зависимы. Тогда
– линейно зависимы. Тогда  R, одновременно не равные нулю:
R, одновременно не равные нулю:  . Если, например,
. Если, например,  , то
, то 

 – диагональ параллелограмма со сторонами, параллельными
– диагональ параллелограмма со сторонами, параллельными  и
и 

 ,
,  ,
,  лежат в одной плоскости, то есть они компланарны.∎
лежат в одной плоскости, то есть они компланарны.∎
Теорема 4. Любые четыре вектора линейно зависимы.
Доказательство. Предположим, что никакие три из векторов  не компланарны (иначе они линейно зависимы) очевидно. Остальное следует из (рис.1.6) по аналогии с доказательством теоремы 4. Через точку D проведем три плоскости, параллельные парам векторов {
не компланарны (иначе они линейно зависимы) очевидно. Остальное следует из (рис.1.6) по аналогии с доказательством теоремы 4. Через точку D проведем три плоскости, параллельные парам векторов {  ,
,  }; {
}; {  ,
,  };{
};{  ,
,  }.
}.

 ,
, 

 .
.  R:
R: 

 ,
,  ,
,  ,
,  – линейно зависимы.∎
– линейно зависимы.∎
Рис.1.6. Иллюстрация доказательства теоремы 4.
Определение 14.Базисом на прямой (соответственно, на плоскости и в пространстве) называется упорядоченный набор из одного (соответственно, из двух и трех) линейно независимых векторов.
Замечание. Очевидно, что рассматриваемые векторы должны быть ненулевыми.
Теорема 5(о существовании и единственности разложения по базису). Всякий вектор пространства (соответственно, плоскости и прямой) однозначно представляется в виде линейной комбинации векторов данного базиса.
Доказательство. Докажем существование искомой линейной комбинации для пространства. Пусть векторы  образуют данный базис, а
образуют данный базис, а  – произвольный вектор. По теореме 4 векторы
– произвольный вектор. По теореме 4 векторы  линейно зависимы, так что существует нетривиальная линейная комбинация
линейно зависимы, так что существует нетривиальная линейная комбинация  . Если
. Если  , то имеем
, то имеем 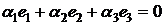 , причем одно из чисел
, причем одно из чисел  , что противоречит линейной независимости
, что противоречит линейной независимости  . Следовательно,
. Следовательно, 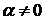 и искомая комбинация имеет вид
и искомая комбинация имеет вид
 .
.
Докажем единственность. От противного. Пусть имеется два различных набора чисел  и
и  таких, что
таких, что  и
и  . Тогда
. Тогда  и в силу линейной независимости
и в силу линейной независимости  имеем
имеем  , что противоречит различию наборов чисел. ∎
, что противоречит различию наборов чисел. ∎
Определение 15.Координатами (компонентами) вектора  относительно базиса
относительно базиса  называются такие (однозначно определенные) числа
называются такие (однозначно определенные) числа  , что
, что
 .
.
Также будем писать 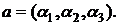
Теорема 6 (операции над векторами, заданными своими координатами). При сложении любых двух векторов  и
и  их координаты (относительно любого фиксированного базиса) складываются; при умножении
их координаты (относительно любого фиксированного базиса) складываются; при умножении  на
на 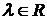 , все координаты вектора умножаются на это число.
, все координаты вектора умножаются на это число.
Доказательство. Пусть 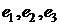 – базис,
– базис,  ,
,  . Тогда в силу свойств операций сложения векторов и умножения вектора на число имеем
. Тогда в силу свойств операций сложения векторов и умножения вектора на число имеем
 ,
, 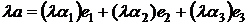 . В силу единственности разложения по базису
. В силу единственности разложения по базису  что теорема доказана. ∎
что теорема доказана. ∎
Дата добавления: 2018-04-05; просмотров: 665; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
