Аффинные и изометрические преобразования
1. Прямоугольник имеет … элементов симметрии.
2. Движением плоскости, не имеющем инвариантных прямых, является …
3. При аффинных преобразования плоскости сохраняются:
3.1. Углы
3.2. Параллельной прямых
3.3. Расстояние между точками
3.4 . Свойство быть окружностью
Проективная плоскость
1. Овальная кривая на проективной плоскости имеет уравнение …
2. Моделью проективной прямой является
2.1. Аффинная прямая
2.2. Окружность
2.3. Окружность с выколотой точкой
2.4. Расширенная прямая.
Задачи для самостоятельного решения.
Эллипс, парабола, гипербола
1. Какому условию должен удовлетворять эксцентриситет гиперболы 
для того, чтобы на правой ее ветви существовала точка, одинакова удаленная от правого фокуса и от левой директрисы.
2. Докажите, что длина перпендикуляра, опущенного из фокуса гиперболы на одну из ее асимптот, равна мнимой полуоси.
3. Докажите, что директрисы гиперболы проходят через основания перпендикуляров, опущенных из соответствующих фокусов на директрисы.
4. Докажите, что площадь параллелограмма, одна из вершин которого лежит на гиперболе, а две стороны на асимптотах, есть величина постоянная, равная половине произведения полуосей гиперболы.
5. Докажите, что произведение длин перпендикуляров, опущенных на ось параболы из концов любой хорды, проходящей через фокус этой параболы, имеет постоянную величину.
6. Найти множество всех точек, каждая из которых симметрична фокусу F параболы относительно некоторой касательной.
|
|
|
7. Кривая второго порядка задана общим уравнением. При каком условии: а) ось ОХ имеет асимптотическое направление; б) ось ОХ является асимптотой данной кривой; в) оси координат являются асимптотами кривой.
Линии и поверхности второго порядка
1. Доказать, что если кривая второго порядка имеет линию центров, то она распадается на пару параллельных или слившихся прямых.
2. Доказать, что если вершины параллелограмма лежат на кривой второго порядка, то центр параллелограмма является центром этой кривой.
3. Доказать, что отрезок любой касательной к гиперболе, заключенный между асимптотами, делится в точке пересечения пополам.
4. Доказать, что отрезок касательной к эллипсу в любой точке, заключенной между касательными, проведенными в вершинах, лежащих на большой оси, виден из фокусов под прямым углом.
5. Показать, что плоскость 
касается параболоида 
, если
.
6. Доказать, что прямолинейные образующие однополостного гиперболоида
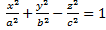проектируются на координатные плоскости в касательные к соответствующим главным сечениям.
7. Доказать, что касательные плоскости, проведенные к поверхности второго порядка в концах одного и того же диаметра, параллельны между собой, и, обратно, если две касательные плоскости одной и той же поверхности параллельны между собой, то точки их прикосновения лежат на одном диаметре.
|
|
|
Дата добавления: 2018-04-04; просмотров: 601; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!