Арифметическое разложение булевых функций
Если в некотором выражении булевой функции F заменить логические операции арифметическими на множестве вещественных чисел {0, 1} по следующим правилам:
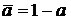 , (7)
, (7)
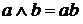 , (8)
, (8)
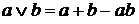 , (9)
, (9)
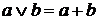 , если
, если 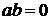 , (10)
, (10)
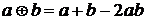 , (11)
, (11)
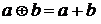 , если
, если 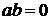 , (12)
, (12)
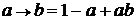 , (13)
, (13)
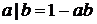 , (14)
, (14)
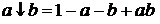 , (15)
, (15)
то полученное в результате такой замены, раскрытия скобок и приведения подобных, выражение называется арифметическим разложением (или арифметическим полиномом) булевой функции 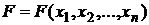 и обозначается черев G(F) .
и обозначается черев G(F) .
Например, для булевой функции, заданной вектором значений таблицы истинности w(F)=(00100111) арифметический полином G(F) имеет вид:
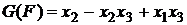 .
.
Отметим некоторые свойства арифметического полинома G(F) булевой функции n переменных 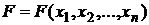 .
.
1. Полином G(F) является для функции F единственным.
2. Полином G(F) имеет степень n, если вектор w(F) содержит нечетное
число единиц.
3. Сумма коэффициентов полинома G(F) равна значению булевой функции
F на наборе переменных (1,1,…,1) в таблице истинности.
Некоторые из методов разложения булевых функций F в канонический полином Жегалкина после соответствующей модификации могут быть применимы для разложения F в полином G(F). К таким методам относятся, в частности, рассмотренный выше метод преобразования СДНФ.
|
|
|
При использовании метода преобразования СДНФ необходимо в СДНФ функции F заменить логическую операцию «дизъюнкция» на операцию "арифметическое сложение", поскольку из (12) следует, что 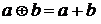 , если
, если 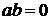 . Затем в полученном выражении необходимо избавиться от отрицания переменных по (7). После раскрытия скобок и приведения подобных получается искомый полином.
. Затем в полученном выражении необходимо избавиться от отрицания переменных по (7). После раскрытия скобок и приведения подобных получается искомый полином.
Пример. Составить арифметический полином G(F) СПНФ булевой функции, если СДНФ данной булевой функции, имеет вид: 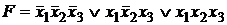 .
.
Решение. Заменим операцию дизъюнкции на операцию "арифметическое сложение" по формуле (10). При этом воспользуемся тем, что произведение (конъюнкция) любых полных дизъюнкций СДНФ всегда равно нулю:
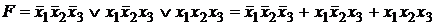 .
.
Все переменные с отрицанием заменяем по формуле (7), затем раскрываем скобки и в полученном выражении приводим подобные:
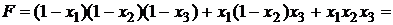
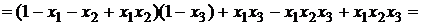
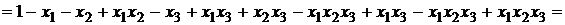
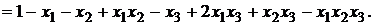
Ответ:G(F) 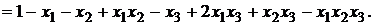
Пример. Составить арифметический полином G(F) СПНФ булевой функции, если СДНФ данной булевой функции, имеет вид: 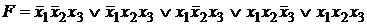 .
.
|
|
|
Решение.
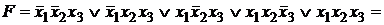
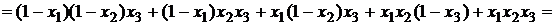
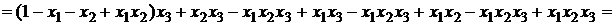
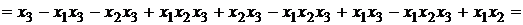
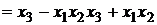 .
.
Ответ: G(F) 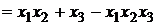 .
.
ЛИТЕРАТУРА
1 Горбатов,В.А. Дискретная математика / В.А.Горбатов, А.В.Горбатов, М.В.Горбатова. – М.: АСТ Астрель, 2006.
2 Горбатов, В.А. Основы дискретной математики / В.А.Горбатов. – М.: Высшая школа, 1986.
3 Новиков, Ф.А. Дискретная математика для программистов / Ф.А.Новиков. – СПб.: Питер, 2007.
4 Плотников, А.Д. Дискретная математика: учебное пособие / А.Д.Плотников. – М.: Новое знание, 2006.
5 Супрун, В.П. Методические указания к семинарским занятиям по специальным курсам «Теория булевых функций» и «Теория автоматов» «Полиномиальное разложение булевых функций» / В.П.Супрун. – Мн.: БГУ, 1991.
6 Шапорев, С.Д. Дискретная математика. Курс лекций и практических занятий / С.Д.Шапорев. – СПб.: БХВ-Петербург, 2007.
7 Яблонский, С.В. Введение в дискретную математику / С.В.Яблонский. – М.: Наука,1988.
СОДЕРЖАНИЕ
Булевы переменные и функции ……………………..…………………..………...….3
Элементарные булевы функции. Равносильности………………………………...…4
Дизъюнктивные нормальные формы ...…………..….………………….………........7
Минимизация ДНФ …………….……………………..………………….……….….10
Конъюнктивные нормальные формы …………….…..…………….…......….…..…13
|
|
|
Минимизация КНФ …………….……………………..………………….……….….16
Полиномиальное разложение булевых функций…..….………………………........19
Разложение булевых функций в канонический полином Жегалкина ......….…..…21 Арифметическое разложение булевых функций........................................................23
Литература……………….…..…….…………………..……………...….…….......….24
Дата добавления: 2018-04-04; просмотров: 1830; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
