Определение эффективности цифровых систем передачисигналов

Лекция №6 «Эффективность и помехоустойчивость цифровых систем передачисигналов по радиоканалам»

Помехоустойчивое кодирование

Практически важный вывод работ Шеннона состоит в том, что если скорость передачи информации меньше пропускной способности канала, то с использованием кодов, исправляющих ошибки, можно создать систему связи со сколь угодно малой вероятностью ошибки на выходе декодера канала. При этом адекватная система без корректирующего кодирования будет более сложной, дорогой и энергоемкой. Отсюда вывод: система, не имеющая корректирующего кодирования и работающая без ошибок, - это крайне неэффективная система. Наоборот, эффективная система должна иметь возможность работы в режиме с достаточно высокой частотой ошибок в потоке на входе декодера, а сам декодированный поток должен иметь крайне малую вероятность ошибки на бит.

Энергетический выигрыш кодирования

Введение при кодировании для исправления ошибок в информационный сигнал избыточных символов сопровождается негативным эффектом - снижением, при неизменной скорости цифрового потока (C_DS), скорости передачи полезной нагрузки (С_inf) обратно пропорционально скорости кода (R): C_DS = C_lnf/R , бит/с. Отсюда следует, что для сохранения скорости передачи полезной нагрузки необходимо расширение полосы частот канала в Rраз или повышение кратности модуляции.Положительным эффектом помехоустойчивого кодирования является либо снижение вероятности ошибки, либо снижение энергетики передачи при той же вероятности ошибки, либо и то, и другое одновременно. Таким образом, кодирование расширяет возможности компромисса между полосой и энергетикой канала, присущего любой системе связи.В качестве примера системных компромиссов рассмотрим воз­можности выбора между кратностью относительной фазовой модуляции К = lg₂M , кодовой скоростью Rи минимально необходимой полосой B_N.

Положим, что кодер источника производит биты информации со скоростью V_b=1/Т_b, где Т_b- длительность информационного символа (тактовый интервал) в системе без кодирования. Тогда в зависимости от кратности модуляции М-позиционного сигнала ФМ требуется полоса Найквиста B_N = 1/КТ_b. При кодировании кодом, исправляющим ошибки, скорость группового потока, состоящего из информационных и проверочных символов, возрастает в1/Rраз и становится равной у = 1/RT_bсоответственно увеличивается и полоса Найквиста В_N=1/KRT_b.Данные расчетов для ряда значений К и R приведены в табл.6.1

Из таблицы следует, что при передаче с неизменной скоростью V_b = const, одно и то же значение полосы Найквиста, например, B_N = 1/2Т_b, обеспечивается для сочетаний (К=2, R=1), (K=3, Д=2/3), (К=4, R=1/2).Какое же сочетание лучше?

Ответ на этот вопрос дает параметр, называемый энергетическим выигрышем кодирования (ЭВК).

Рассмотрим случай, когда передача в системах без кодирования и с кодированием производится при неизменной средней мощности Р_ср.В системе без кодирования вычисленная энергия одного бита информа­ции составляет Е_b = P_cp/V_b. В системе с кодированием за счет увеличения общего числа символов энергия одного бита кодированного потока снижается до значения E_С = RE_b <Е_b и Р_ср = E_СV_С.

Таблица 6.1

Пусть в канале действует аддитивный белый гауссовский шум с односторонней спектральной плотностью мощности N0. Тогда отношение мощности модулированного сигнала к мощности шума на выходе приемного фильтра с полосой Найквиста (обычно называемое отношением несущая/шум) равно:C/N=ECVC/NOBN=EC/NO=(Eb/NO)R     (6.1)

так как в этом случае V_Cчисленно равна B_N, или в логарифмическом виде:

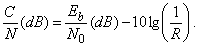
(6.2)

Формула (6.2) показывает, что для некоторой вероятности ошибки значение отношения C/Nможет быть на 10lg(1/R) ниже, чем значение отношения E_b/N₀ для той же вероятности ошибки в системе без кодирования. Эта величина является некоторой постоянной составляющей энергетического выигрыша кодирования и иногда называется выигрышем производительности.

  Рис.6.1.

Реально достижимый ЭВК зависит, в первую очередь, от свойств корректирующего кода и алгоритма его декодирования. В качестве примера определения ЭВК на рис. 6.1 показаны характеристики вероятности ошибки от отношения E_b/N₀ для системы ФМ с кодированием и без него. Разница значенийE_b/N₀ между двумя кривыми по горизонтали при фиксированной вероятности ошибки (на рис.6.1 – для значений 10^-3 и 10^-5) и есть ЭВК (G_C).Значение реального ЭВК зависит от той вероятности ошибки Р_е, при которой он определяется. При возрастании C/N(снижение вероятности ошибки) ЭВК увеличивается, но до определенных пределов. Верхней границей реального ЭВК является асимптотический ЭВК, который определяется как: G_A=10lg(Rd_f)    (6.3)             

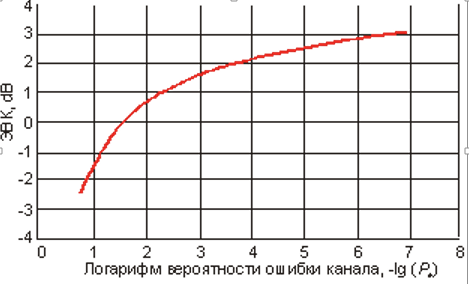Рис.6.2.

где d_f – свободное расстояниесверточного кода.

Типичная зависимость ЭВК от вероятности ошибки канала показана на рис.6.2, где кривая соответствует использованию сверточного кода с R = 1/2, d_f = 5 для асимптотического ЭВК, равного 3,98 dB.

Определение эффективности цифровых систем передачисигналов

Спектральная эффективность

Спектральная (частотная) эффективностьцифровой системы определяется, как

                                                      γ =R_b/B_W (6.4)

где R_b- скорость передачи информации, бит/с;

B_W— полная полоса частот канала, Гц.

Измеряется спектральная эффективность числом битов в секунду, приходящихся на 1 Гц полосы канала, т.е. бит/(с·Гц).

В реальных условиях доступная полоса частот канала B_Wпо тем или иным причинам может использоваться не полностью, поэтому даже достаточно эффективная система передачи в ее конкретном применении по данному критерию оценки будет выглядеть неэффективной. Кроме того, необходимо уточнить критерий спектральной эффективности, связав его с полосой Найквиста B_Nи коэффициентом скругления спектра α, значение которого характеризует расширение практически занимаемой спектром сигнала полосы частот канала B_L сверх полосы Найквиста B_N

BL =BN(1+ α)                                                               (6.5)

Соответственно реальная спектральная эффективность ηразличных схем модуляции, предназначенных для цифровой передачи, выражается формулой:

η= RbBL=Rb/BN(1+ α)                                                  (6.6)

В идеальном случае при полном использовании всей полосы частот канала, когда B_W = В_L, показатели эффективности ηи γ совпадают, т.е. γ = η.

Целесообразно ввести также критерий потенциальной спектральной эффективности конкретного метода модуляции, который соответствует коэффициенту η или γпри BW = ВL и α = 0.Определим потенциальную эффективностькак: γ 0=Rb/ BN (6.7)
Отсюда следует, чтоη= γ 0/(1+ α) или γ 0= η(1+ α)                                      (6.8)

При использовании многопозиционной цифровой модуляции

Rb=lg2(M)RS                                                                        (6.9)

где М- число элементов пространства сигналов при цифровой модуляции;

R_S- скорость передачи символов цифрового потока.

Согласно критерию Найквиста максимальная скорость передачи символов в полосовой системе численно равнаRS= BW/(1+ α)                        (6.10)

Следовательно, при B_W = В_Lη=lg₂(M)/(1+ α)                                                      (6.11)

Отсюда следует, что для повышения спектральной эффективности ηнеобходимо увеличивать кратность модуляции lg₂(M) и одновременно снижать значение коэффициента скругления спектра α, тем самым уве­личивая крутизну среза спектра модулирующего сигнала. Использование малых αтребует разработкисложных цифровых фильтров,а при приеме отсчеты сигнала в решающем устройстве становятся в большей степени подвержены временному джиттеру. Дополнительно к этому возрастает чувствительность к нелинейным искажениям в тракте, которые проявляются в снижении раскрыва глазка принимаемого сигнала, поэтому ограничиваются значением αв пределахот 0.4 до 0.6.В системах цифрового ТВ вещания реально используются значения α, равные 0.15; 0.25; 0.35.

Для систем с модуляцией OFDM эффективность передачи определяется как

η=2/(1+α/L)

где L – число параллельно передаваемых в системе с OFDM потоков данных( не число ортогональных несущих).

Увеличение числа параллельных каналов данных приводит к высоким значеничям эффективности ηбез снижения коэффициента α, что и являетсяодним из премуществ модуляции OFDM.

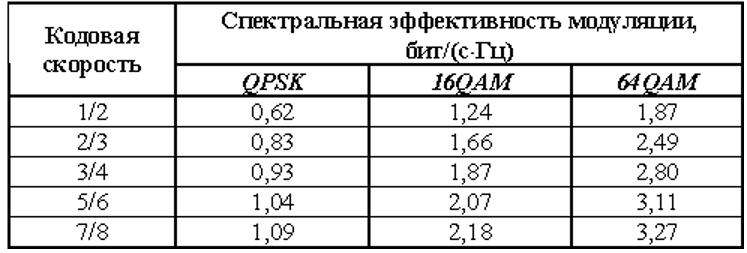
При современном уровне сжатия сигналов изображения для переда­чи одной программы ТВЧ или нескольких программ стандартного качества требуется скорость потока около 20 Мбит/с. Ранее отмечалось, что для согласования этой скорости со стандартными полосами частот 6, 7 и 8 МГц существующих в мире ТВ каналов, необходимо применять сочетание многопозиционной модуляции с помехоустойчивым кодированием. В нормальных условиях системные компромиссы обеспечиваются при спектральной эффективности около 4 бит/(с·Гц). Однако при недостаточной помехозащищенности канала связи приходится снижать кратность модуляции и повышать избыточность из-за увеличения доли символов корректирующего кодирования, при этом соответственно снижается пропускная способность и, как следствие, падает спектральная эффективность. В зависимости от кратности модуляции и кодовых скоростей, принятых в цифровом наземном ТВ вещании, значения спектральной эффективности могут изменяться в очень широких пределах, что показано в табл. 3 для некоторых типичных случаев использования неиерархической модуляции в канале с полосой 8 МГц.

Таблица 6.2 Спектральная эффективность 6.2.2.Энергетическая эффективностьПоказатель энергетической эффективности β=RbNO/PC(6.12)

где Р_С- средняя мощность модулированного сигнала;

N0 = kT- односторонняя спектральная плотность мощности адди­тивного белого гауссовскогошума на входе приемного фильтра.С учетом того, чтоРС=EbRb (6.13)
где Еb- энергия сигнала на бит информации на входе приемного фильтра, получаемβ=NO/Eb(6.14)

Таким образом, коэффициент β- величина обратная отношению энергии на бит в передаваемом сигнале к плотности шума на входе приемника.

При использовании в модеме согласованной фильтрации и формировании спектров, согласно критериям Найквиста, энергетическая эффективность βможет быть выражена следующим образом:β=RbNOBN/ РСBN                                                               (6.15)

Так как при согласованной найквистовской фильтрации шумовая полоса приемника совпадает с полосой Найквиста, то мощность шума на входе решающего устройства равна Р_Ш = N_oB_N, при этом отношение сигнал/шум q = Р_C/Р_Ш, а b = R_b/B_Nq.

Коэффициенты ηи βвзаимосвязаны. Подставляя в формулу для β отношение Rb/BN = γ0 = η(1+α), получаемβ = η(1+α)/q                                                              (6.16)

 

q = η(1+α)/ β                                                                 (6.17)
Как известно, пропускная способность (максимально возможная скорость передачи информации) частотно-ограниченного канала с аддитивным белым гауссовским шумом определяется формулой Шеннона:C=ΔFlg2(1+PC/NOΔF)                                    (6.18)

Здесь под полосой пропускания системы ΔFследует понимать шумовую полосу, равную полосе Найквиста B_N. В пределе, при выполнении условий теоремы, R_b = С, и тогда можно получить соотношение для верхней границы эффективности передачи информации

R_b/B_N=lg₂(1+q)=lg2(1+η(1+α)/ β)                                         (6.19)

η(1+α)=lg2(1+ η(1+α)/ β)                                                   (6.20)

 

Найдем отсюда формулу для энергетической эффективности βкак функции реальной спектральной эффективности ηи коэффициента скругления спектра α

---

Дата добавления: 2018-04-04; просмотров: 571; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!