Переходный процесс в цепи с последовательно

Соединенными резистором и конденсатором

Рассмотрим переходный процесс при включении цепи RC к источнику постоянного напряжения (рис. 9.4).

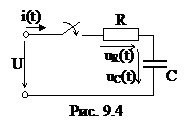После замыкания ключа происходит процесс заряда конденсатора до величины напряжения U источника питания. В течение этого времени в цепи протекает ток, который после полной зарядки конденсатора становится равным нулю. Это физическое понимание переходного процесса. Опишем процесс математически.

В соответствии со вторым законом Кирхгофа составим уравнение электрического состояния для рассматриваемой цепи относительно напряжения конденсатора:

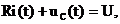
или с учетом того, что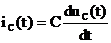

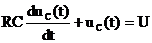Решение этого дифференциального уравнения находится как сумма принужденной и свободной составляющих: u_С(t) = u_Спр(t) +u_Ссв(t) = U+ Вe^pt .

Характеристическое уравнение для этой схемы: RCp + 1=0,

корень этого уравнения

p = -1/(RC).

Постоянная времени переходного процесса .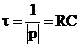

Постоянную интегрирования В найдем, рассмотрев искомую функцию в момент времени t=0. Так как схема до коммутации была отключена от источника питания, то есть конденсатор не был заряжен, то согласно второму закону коммутации начальное значение напряжения на конденсаторе u_С(0+) = u_С(0-) = 0.

Так как u_С(0+)= U + B =0, то В = u_c(0+) – U = –U.

Искомая переходная функция имеет вид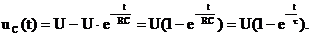

Ток в цепи

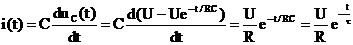Напряжение на резистивном элементе

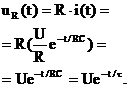
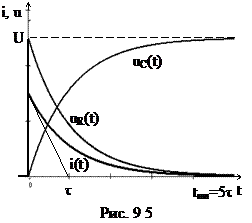
Графики переходных функций тока и напряжений представлены на рис. 9.5.

Переходные процессы в неразветвленной цепи R, L, С

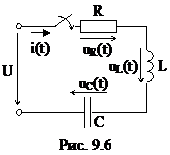Пусть к источнику постоянного напряжения U подключается цепь с последовательным соединением элементов R, L, C (рис. 9.6). Для послекоммутационной схемы (ключ замкнут) можно составить уравнение по второму закону Кирхгофа в дифференциальной форме:

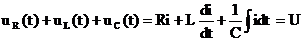Дифференцируя это уравнение по времени, получим дифференциальное уравнение второго порядка с постоянными коэффициентами, составленное относительно тока в цепи:

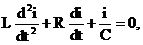
так как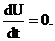

Так как правая часть уравнения равна нулю, то принужденная составляющая тока отсутствует и переходный ток имеет только одну свободную составляющую:

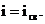
Вид свободной составляющей определяется видом корней характеристического уравнения.

Составим характеристическое уравнение для данного дифференциального уравнения:

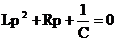или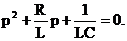

Корни такого уравнения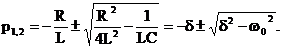

Знак подкоренного выражения определяет характер свободного процесса.

Если 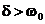, то корни действительные, разные, отрицательные и в этом случае характер свободного процесса называют апериодическим, а решение дифференциального уравнения имеет вид:

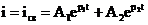где А₁ и А₂ – вещественные постоянные интегрирования, определяемые из начальных условий.

Продифференцируем решение дифференциального уравнения по времени:

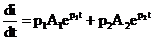Запишем решение дифференциального уравнения и его производную для момента времени t=0+:

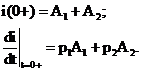
Так как согласно первому закону коммутации

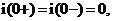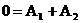то или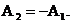

Значение 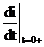найдем из уравнения, составленного по второму закону Кирхгофа для момента времени t=0+:

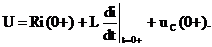
Так как согласно законам коммутации i(0+)=0 и u_C(0+)=0, то

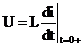или .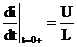

Следовательно,

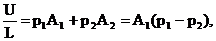
откуда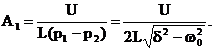

Переходные функции тока в цепи и напряжений на элементах R, L, C:

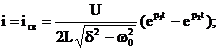
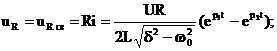
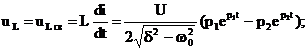
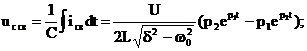
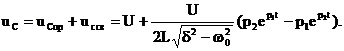
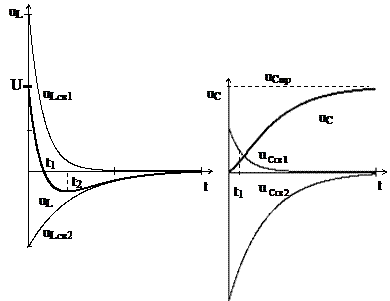
Кривые зависимостей i(t), u_L(t), u_C(t) приведены на рис. 9.7 и 9.8 а, б.

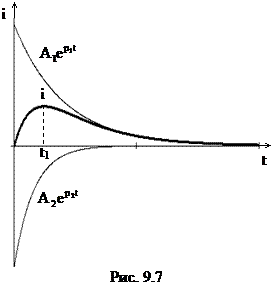Переходный ток i(t) состоит из двух экспоненциальных составляющих (рис. 9.7) с различной степенью затухания. Время t₁ достижения током его максимального значения можно определить, приравняв к нулю производную di/dt функции. Кривые u_L(t) и u_C(t) также состоят из двух экспоненциальных составляющих (рис. 9.8, а, б).

Напряжение u_L убывает от значения U, переходит через ноль в момент времени t₁, когда ток максимален, затем возрастает до некоторого отрицательного максимума, после чего стремится к нулю.

а) б)

Рис. 9.8

Напряжение u_С монотонно возрастает от нуля до значения равного напряжению источника U, причем точка перегиба кривой при t=t₁ получается когда ток достигает максимума.

При 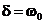корни характеристического уравнения действительные, одинаковые, отрицательные .

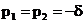В этом случае общее решение однородного дифференциального уравнения имеет вид

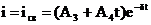а ее производная

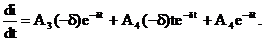
При t=0+ эти выражения запишутся, учитывая значения начальных условий: ;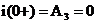

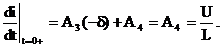
Переходный ток в этом случае имеет вид

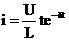а напряжения на элементах R, L, C определяются:

;

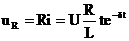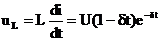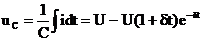Характер изменения тока и напряжений на элементах цепи не будет отличаться от того, что мы наблюдали при 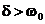. Переходный процесс в этом случае является предельным апериодическим процессом и носит название критического. Из условия 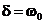можно определить критическое сопротивление контура 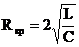, при котором имеет место критический режим.

При 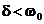корни характеристического уравнения комплексно-сопряженные:

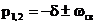где 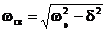- угловая частота свободных колебаний контура.

Переходный процесс в этом случае называется колебательным.

Решение однородного дифференциального уравнения в этом случае записывается:

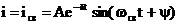а производная этой функции:

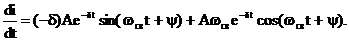
При t=0+ эти функции имеют вид:

;

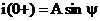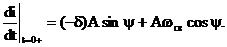
Так как начальные условия такие же, как и в предыдущих случаях, то

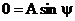, откуда ψ=0 и

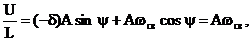
тогда .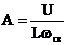

Переходная функция тока запишется:

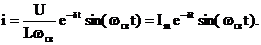
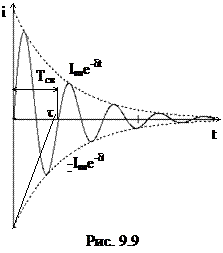То есть ток совершает затухающие колебания около нулевого значения (рис. 9.9).

Время переходного процесса t_пп зависит от величины постоянной времени, которая в данном случае может быть определена как 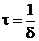, тогда .

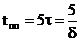Период затухающих колебаний определяется частотой свободных колебаний 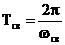. Определить количество колебаний можно, сравнив время переходного процесса и период свободных колебаний.

Напряжение на индуктивном элементе

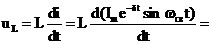
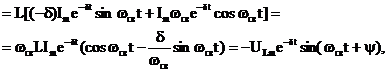
где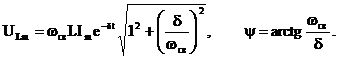

Составим дифференциальное уравнение, где в качестве неизвестного выступает напряжение емкостного элемента u_C:

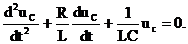
Решение этого уравнения

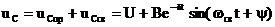Продифференцируем это выражение

Для момента времени t=0+ эти выражения с учетом независимых начальных условий запишутся:

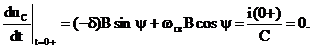
Из первого уравнения получим 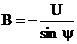, тогда

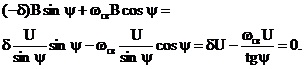
Откуда .

Искомая функция имеет вид

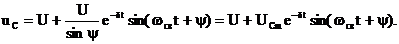
Кривая переходной функции u_C показана на рис. 9.10.

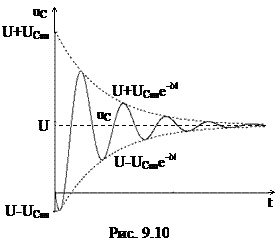Из рис.9.10 видно, что напряжение колеблется около своего установившегося значения U и не может превзойти значения двойного напряжения 2U. Оно достигает максимального значения примерно через половину периода после включения цепи. Этим пользуются в импульсной технике для получения напряжения на конденсаторе, равного двойному значению напряжения источника питания.

ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ

Для получения устойчивой картины переходного процесса на экране осциллографа исследуемые цепи подключают к источнику прямоугольных импульсов – транзисторному ключу (рис. 9.11, а), форма выходного сигнала которого показана на рис.9.12. Амплитуда выходного сигнала транзисторного ключа U_m=10 B.

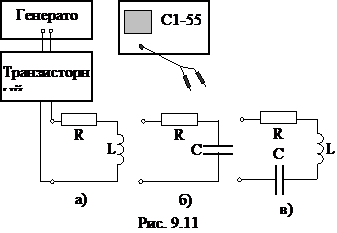
Транзисторный ключ управляется звуковым генератором (рис. 9.11, а). Частота коммутации ключа равна частоте сигнала генератора. Для исследования цепи важен момент коммутации и интервал времени до следующего включения.

Для того чтобы за время, равное половине длительности прямоугольных импульсов, переходный процесс успевал завершиться, необходимо выполнение условия t_пп≤Т/2. А так как t_пп = 5τ, то длительность прямоугольно импульса определяется как Т/2 = 5τ или Т = 10τ. Частота прямоугольных импульсов (частота сигнала генератора) f= 1/T.

Для экспериментального снятия кривых переходного процесса используется осциллограф С1-55, позволяющий учитывать масштабы напряжения и времени.

Резистор с сопротивлением R представляет собой магазин сопротивлений 0 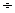10000 Ом.

Конденсатор с емкостью С - блок конденсаторов универсального стенда 0 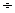34.75 мкФ.

Катушка с индуктивностью L - обмотка однофазного универсального трансформатора на разомкнутом сердечнике из комплекта стенда: катушка с разомкнутым сердечником: клеммы 2-3 – L=0,5 Гн; клеммы 1-3 – L=0,16 Гн; клеммы 1-2 –L=0,18 Гн. Катушка без сердечника: клеммы 2-3 – L=0,016 Гн; клеммы 1-3 – L=0,09 Гн.

Дата добавления: 2018-04-04; просмотров: 765; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!