Изображение синусоидальных функций (напряжение, сила тока, мощность) векторами на комплексной плоскости
Расчет сложной разветвленной цепи может быть существенно упрощен, если заменить синусоидальные токи и напряжения векторами, расположенными на комплексной плоскости. Такой метод получил название метода комплексных амплитуд.
В основе данного метода лежит формула Эйлера:
 , (2.21)
, (2.21)
где j =  .
.
Умножив обе части на А, получим: A  = A1+A2,
= A1+A2,
где A = 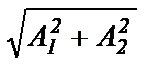 - модуль комплексного числа;
- модуль комплексного числа;  - аргумент комплексного числа.
- аргумент комплексного числа.

Рис.2.9. Изображение вектора  на комплексной плоскости
на комплексной плоскости
(w - угловая частота вращения вектора  )
)
Поскольку в формуле Эйлера a может быть любым, мы сделаем его линейной функцией времени:
a = wt + y. (2.22)
Тогда:  . (2.23)
. (2.23)
Полученный результат (2.24) показывает, что синусоидальная функция времени есть мнимая часть некоторого комплексного числа:
а = Asin(wt +y) = ImAej(wt+y); (2.24)
при условии, что t = 0 получим:
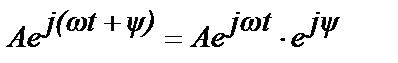 Þ
Þ 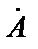 = A
= A  (2.25)
(2.25)
Векторная диаграмма - диаграмма векторов на комплексной плоскости, построенная с учетом их взаимной ориентации по фазе.
Если вектора вращаются на плоскости с одинаковыми частотами w, то их взаимное положение не меняется, это свойство позволяет исключить из рассмотрения сам факт их вращения, то есть принимать t = 0.
В качестве примера на рис.2.10 изображена операция умножения некоторого вектора  на оператор поворота j.
на оператор поворота j.
|
|
|
Пусть модуль  = 10А. Его положение на комплексной плоскости зависит от значения аргумента. Значениям y = 0, 900, - 900 соответствуют комплексные числа
= 10А. Его положение на комплексной плоскости зависит от значения аргумента. Значениям y = 0, 900, - 900 соответствуют комплексные числа  :
:
 ;
;  ;
;  .
.
По формуле Эйлера:
 ;
;  ;
;  ;
;  .
.

Рис.2.10. Умножение вектора на +j и –j
Основы символического расчета цепей синусоидального тока
Этот метод позволяет перейти от дифференциальных уравнений, составленных для мгновенных токов, напряжений и т.д., к алгебраическим уравнениям, составленным для соответствующих им комплексных изображений.
Последовательное соединение

Рис.2.11. Последовательное соединение R, L, C
На основании второго закона Кирхгофа:
u = uR + uL + uC;
u = iR +L  +
+  . (2.26)
. (2.26)
Перейдем к комплексным изображениям действующих значений:
i = Imsin(wt+yi) Þ  . (2.27)
. (2.27)
Используя полученный комплекс тока, определим комплексы падения напряжения  на всех участках цепи:
на всех участках цепи:
Для сопротивления:
 , (2.28)
, (2.28)
Для индуктивности:
 , (2.29)
, (2.29)
Для емкости:
 . (2.30)
. (2.30)
Найденные комплексы напряжений подставим в исходное уравнение:
 , (2.31)
, (2.31)
 . (2.32)
. (2.32)
– получен закон Ома в комплексной форме.
Выражение в знаменателе представляет собой комплексное сопротивление исходной цепи, которое имеет вещественную и мнимую составляющую.
|
|
|
 , (2.33)
, (2.33)
где  ;
;  .
.
Для комплексных амплитуд закон Ома запишется в следующем виде:
 , (2.34)
, (2.34)
где Um= Imz - амплитуда напряжения;

Рис.2.12. Изображение сопротивления на комплексной плоскости
φU = j + ji; Þ j = jU – ji; (2.35)
u(t) = Umsin(wt + jU). (2.36)
Построим векторную диаграмму цепи.

Рис.2.13. Векторная диаграмма для последовательного соединения разнородных элементов
i(t) = Imsin(wt + ji); ji > 0.
Построение векторной диаграммы начинают с вектора тока, т.к. он один и тот же на всех участках цепи. Из построенной на комплексной плоскости векторной диаграммы можно выделить векторный треугольник напряжений, представленный на рис.2.14.

Рис.2.14. Векторный треугольник напряжений
Ниже приведен треугольник сопротивлений.

Рис.2.15. Скалярный треугольник сопротивлений
Угол сдвига фаз между напряжением и током можно определить из любого треугольника.
 . (2.37)
. (2.37)
Дата добавления: 2018-04-04; просмотров: 276; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
