Глава 3. Моделирование технологических объектов, управляемых АСУТП

Алгоритмы функционирования

Что бы решать задачи управления технологическим объектом (ТО), следует достаточно точно и полно знать его свойства и характеристики, обеспечивающие нормальное течение технологического процесса. Характеристики объекта, обеспечивающие управление им, будем называть управляющими(входными) параметрами, а интересующие нас параметры техпроцесса будем называть выходными параметрами. Основной задачей управления будем считать изменение управляющих параметров по закону, обеспечивающему работу технологического объекта в соответствии заданным критерием оптимальности. Для решения этой задачи необходимо знать зависимость между управляющими и выходными параметрами техпроцесса в условиях действия различных возмущений. Достаточно точное и математически обоснованное описание зависимости между управляющими (входными) и управляемыми (выходными) параметрами ТО называется алгоритмом функционирования. Если алгоритм функционирования реализован в виде компьютерной программы или на моделирующей установке иного типа, то его называют моделью технологического объекта. Алгоритм функционирования, оформленный в виде совокупности математических выражений, называют математической моделью. При построении модели ТО алгоритм функционирования исследуемого ТО обычно расчленяют на отдельные математически однородные элементы, называемые типовыми звеньями. Этот процесс носит название декомпозиции алгоритма.

После этого модель ТО строится в виде совокупности типовых звеньев, объединенных характерными для данного ТО связями. Далее проводится исследование функционирования ТО путем подачи на модель типовых для данного ТО возмущений. Пригодность полученной модели для описания исследуемого ТО может быть оценена путем вычисления величины I суммарного квадратичного отклонения данных расчета на модели Y_p от результатов экспериментального исследования ТО Y_э:

(3.1)

Чем меньше величина I, тем удачнее модель.

Аналитические методы моделирования

Многообразие технологических процессов обусловило многообразие моделей ТО и методов их получения. Последние подразделяются на аналитические и экспериментальные. Аналитические методы базируются на знании физических, химических и прочих законов, определяющих функционирование технологического объекта. Если теоретических знаний недостаточно, то применяются экспериментальные методы, когда параметры моделей определяются опытным путем. При составлении алгоритма функционирования аналитическим путем технологический объект представляют в виде совокупности типовых звеньев, в каждом из которых происходит однократное преобразование энергии. Звенья такого рода принято называть динамическими звеньями. Они описываются дифференциальными уравнениями не выше второго порядка.

Математическое описание звеньев данного типа производится в следующем порядке.

1) Выходной параметр рассматриваемого звена назовем преобразуемым продуктом Q, а управляющий (входной) параметр – разностью потенциалов U, измеряемой количеством энергии, затрачиваемой на единицу преобразуемого продукта.

2) Описываемое звено представим в виде контура, в котором сумма разностей потенциалов должна быть равна нулю:

. (3.2)

3) Связи между отдельными звеньями, отображающими ТО, формируются исходя из условия равенства нулю суммы расхода продукта в любом разветвлении

. (3.3)

В качестве примера рассмотрим уравнения характерных для систем электромеханического преобразования энергии электрического и механического звеньев.

1) Уравнение цепи якоря двигателя постоянного тока

где u – напряжение, приложенное к цепи якоря;

е_я – ЭДС якоря, причем предполагается, что положительное направление ЭДС якоря противоположно положительному направлению напряжения;

L_я и R_я – индуктивность и активное сопротивление в цепи якоря;

q – переносимый электрический заряд.

2)Уравнение механического звена двигателя, работающего в условиях наличия сухого (M_с) и вязкого трения с коэффициентом вязкости b_c

где j – угол поворота вала двигателя, а положительное направление момента M_с выбирается противоположным положительному направлению момента двигателя M.

В первом примере имеем: Q_j – это переносимый заряд q, U_j – это ЭДС и падение напряжения в рассматриваемом контуре; во втором примере Q_j – это угол поворота j, U_j – это момент двигателя и моменты сопротивления в рассматриваемом механическом звене.

Полный алгоритм функционирования ТО получают путем установления связей между входящими в его состав динамическими звеньями. В результате получают многоконтурную модель, которая будет представлена в виде односвязной или многосвязной системы. Односвязная (одномерная) система получается тогда, когда модель ТО имеет один вход и один выход. Однодвигательные электроприводы, особенно электроприводы постоянного тока, чаще всего отображаются односвязными моделями. Однако электроприводы и другие ТО, входящие в состав АСУТП, обычно объединены различными связями в один комплекс. Их совместную работу невозможно рассматривать раздельно, без учета их взаимодействия и взаимовлияния. Поэтому алгоритм функционирования ТО, управляемого от АСУТП, обычно представляется в виде многосвязной (многомерной) системы, в которой учтено взаимодействие входных параметров, их совместное воздействие на выходные параметры и перекрестные обратные связи от выходных параметров, действующие в ТО. Для анализа подобных систем строят математические модели в матричной форме.

Рассмотрим, например систему уравнений, отображающую некий ТО в виде трехсвязной (трехмерной) линейной системы:

, (3.4)

где – входные переменные, – выходные переменные, а a_ij и b_ij – коэффициенты (некоторые из них могут быть равны нулю). Слагаемые с x₂ и с x₃. а также с y₂ и с y₃, имеющиеся в первом уравнении системы (3.4), отображают объективно существующие в данном ТО перекрестные связи между его параметрами. Аналогичные связи отображены и в остальных уравнениях системы (3.4). Так, слагаемое b₃₂x₂ в третьем уравнении отображает, возможно нежелательное, но объективно существующее перекрестное влияние управляющего воздействия x₂, предназначенного для управления параметром y₂, на параметр y₃, а слагаемое a₂₃y₃ во втором уравнении отображает перекрестную обратную связь с выхода y₃ на параметр y₂. Если коэффициенты b₃₂ и a₂₃ равны нулю, то это означает, что указанные перекрестные связи отсутствуют.

С помощью системы уравнений типа (3.4) можно анализировать как статические, так и динамические режимы, если при анализе динамики заменить дифференциальные уравнения их операторными отображениями. В матричной форме данная система отображается так:

AY=BX , (3.5)

где A, B, X, и Y – записанные в табличной форме (в виде матриц) коэффициенты и переменные системы (3.4):

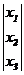А= В= X= Y=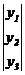

Решение уравнений, записанных в матричной форме, облегчается наличием специализированного программного обеспечения операций с матрицами, предназначенного для исследования систем автоматизации.

Во многих случаях модели ТО существенно нелинейны. В качестве примера рассмотрим трехмерную систему уравнений, описывающих движение механизма по прямой линии со скоростью v из начала координат в точку с координатами x,y и z:

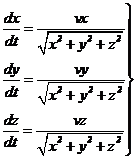(3.6)

Уравнения (3.6) задают проекции скорости v перемещения рабочего органа в пространстве на координаты x,y и z в пределах текущего кадра программы. Уравнения такого типа используются в системах ЧПУ при вычислениях промежуточных точек заданной траектории движения, когда движение между заданными точками должно производиться по прямой линии (линейная интерполяция). Система уравнений (3.6) соответствует случаю, когда начало координат совмещается с начальной точкой очередного линейного участка траектории (с начальной точкой кадра программы), а координаты x, y и z соответствуют конечной точке в данном кадре, что соответствует заданию перемещений в приращениях. Общий вид траектории движения определяется законом изменения координат x,y и z от кадра к кадру. Чтобы пользоваться типовыми программами решения уравнений, записанных в матричной форме, нелинейные уравнения линеаризуются в окрестности интересных для исследования поведения технологического объекта точек.

Дата добавления: 2018-04-04; просмотров: 279; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 6 7 8 9 101112 13 14 15 Следующая ⇒

Мы поможем в написании ваших работ!