Экспериментальные методы получения моделей технологических объектов
Одномерные модели
Экспериментальное исследование технологических объектов и входящих в их состав звеньев обычно имеет целью подтверждение правильности моделей, составленных аналитическими методами. Однако возможны случаи, когда аналитическая модель отсутствует. Это возможно, если объект недостаточно изучен или если разработка аналитической модели до проведения экспериментальных исследований слишком трудоемка и экономически не оправдана. В таких случаях ставится задача получения моделей на основе обработки результатов эксперимента.
Процесс установления соответствия итогов экспериментальных исследований теоретическим представлениям об исследуемом объекте принято называть идентификацией (опознаванием) объекта. Этот термин введен в немалой степени потому, что результаты экспериментальных исследований зависят от ряда трудно учитываемых факторов, многие из которых имеют случайный характер. К таким факторам относятся:
· разброс параметров изучаемых объектов;
· изменение параметров объектов в процессе испытаний, в том числе и отказы оборудования;
· разброс параметров обрабатываемых заготовок и материалов;
· разброс показаний (погрешности) измерительной аппаратуры.
Действие указанных факторов приводит к тому, что при одних и тех же входных (управляющих) воздействиях в разных сериях испытаний значения выходных параметров испытуемого объекта получаются различными. При моделировании технологического объекта по результатам экспериментальных исследований возникает задача оценки разброса выходных параметров и определения их однозначной (детерминированной) зависимости от управляющих воздействий в условиях действия случайных факторов. Для получения надежной детерминированной модели технологического объекта в условиях разброса результатов экспериментальных исследований используют методы теории вероятностной (см. приложение 2), на которых основан регрессионный анализ результатов эксперимента.
|
|
|
Регрессией выходного параметра y на входной параметр x мы будем называть любую функцию f(x), приближенно представляющую вероятностную зависимость y от x. В результате функция y представляется в виде суммы:
y=f(x)+h(x, y)
где h (x, y) – поправочный член.
На первый план обычно выдвигается задача определить, как в среднем изменяется величина y при изменении управляющего воздействия x. Эта задача лучше всего решается с помощью функции регрессии y=g(x), где
 , (3.7)
, (3.7)
где m – количество различных значений y, полученных из опытов, произведенных при заданном значении x;
 - значения y, полученные при заданном значении x;
- значения y, полученные при заданном значении x;
|
|
|
 (
(  ) – условная вероятность того, что y=yj при заданном значении x.
) – условная вероятность того, что y=yj при заданном значении x.
При практическом определении y=g(x) исходят из соотношения;
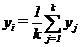 , (3.8)
, (3.8)
где k – количество произведенных измерений величины y при x=xi.
При k→∞ имеет место yi→g (xi).
Функция регрессии g(x) отличается тем, средний квадрат отклонения ее от искомой функции y(x) меньше среднего квадрата отклонения y от любой другой функции f(x), приближенно представляющей вероятностную зависимость y(x). В общем случае функция регрессии имеет нелинейный характер, в связи с чем возникает задача ее линеаризации. Наилучшем линейным приближением вероятностной зависимости y(x) является линейная регрессияy на x, которая может быть представлена в таком виде:
 , (3.9)
, (3.9)
где y0 - среднее значение y в заданном диапазоне измерения x:
 , (3.10)
, (3.10)
x0 - среднее значение x в заданном диапазоне:
 , (3.10’)
, (3.10’)
n – количество экспериментальных точек y(x) на аппроксимируемом интервале;
Sy и Sx – несмещенные стандартные отклонения y и x от их средних значений:
 , (3.11)
, (3.11)
 , (3.11’)
, (3.11’)
r – эмпирический коэффициент корреляции:
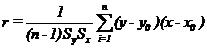 . (3.12)
. (3.12)
Зависимость (3.9) называют эмпирической прямой регрессии, причем коэффициент r, который принимает значения  , показывает, насколько хорошо в среднем может быть представлена величина y в виде линейной функции от x. Если все экспериментальные точки y(x) лежат на одной прямой, то │r│=1, а линейная зависимость y(x) является абсолютно точной. При r=0 величины y и x являются некоррелированными. Отсюда следует, что при малых r связывать y и x линейной зависимостью не имеет смысла.
, показывает, насколько хорошо в среднем может быть представлена величина y в виде линейной функции от x. Если все экспериментальные точки y(x) лежат на одной прямой, то │r│=1, а линейная зависимость y(x) является абсолютно точной. При r=0 величины y и x являются некоррелированными. Отсюда следует, что при малых r связывать y и x линейной зависимостью не имеет смысла.
|
|
|
Пример 3.1. В таблице 3.1 приведена зависимость тока I, потребляемого нагревательным элементом, от напряжения U на его клеммах. Данные записывались один раз в сутки. Числа m показывают, сколько раз записывались одинаковые пары U и I. Считая зависимость I (U) линейной, определить сопротивление Rн нагревательного элемента.
Таблица 3.1

Обозначаем U=x, а I=y и по формулам 3.10-3.12 (учитывая, что общее количество точек I (U); с учетом m, равно 26,т.е. n=26) определяем: x0=25,5; y0=0,248; Sx=1,49; Sy=0,0185; r=0,793.
Соответственно линейная регрессия y на x согласно (3.9), такова:

После упрощения и возврата к U и I получим I≈0,0098 U;  Ом.
Ом.
Если линейная регрессия неудовлетворительна (коэффициент корреляции r близок к нулю), то применяют более точные аппроксимации уравнения регрессии (3.7) с помощью полинома вида
 , m>1,
, m>1,
называемого параболической регрессией порядка m, или с помощью функции
|
|
|
y=aebx,
называемой экспоненциальной регрессией, особенно полезной при идентификации поведения технологического объекта в динамике. Коэффициенты аппроксимирующих функций выбирают таким образом, чтобы было минимизировано суммарное квадратичное отклонение вида (3.1) избранной регрессии от экспериментальных данных.
Многомерные модели
До сих пор мы рассматривали идентификацию одномерных объектов, моделируемых функциями одного переменного. Такой подход применим, в основном, при моделировании отдельных звеньев технологических объектов. Последние же являются, как правило, многосвязными, многомерными системами. Модели таких объектов получают посредством факторного анализа, который называют также методом планирования эксперимента. Данный метод базируется на линейной аппроксимации функций исследуемых объектов. Ввиду разброса результатов экспериментальных исследований многомерная линейная модель формируется как линейная регрессия моделируемого выходного параметра y на управляющие (входные) параметры x1, x2,…xm.
Уравнение линейной регрессии y на x1, x2,…xm записывается в таком виде:
 ,
, 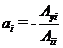 , (3.13)
, (3.13)
где Λyi и Λji – обобщенный корреляционный момент, и обобщенная дисперсия, выраженные в матричной форме;
y0 и xi0 - средние значения y и xi, рассчитанные по формулам (3.10) в заданном диапазоне изменения y и xi.
Факторы x1, x2,…xm, существенно влияющие на выходной параметр y, обычно представляют в относительных величинах:
 , (3.14)
, (3.14)
где ∆xi=ximax-xi0 ;
ximax - максимальное запланированное значение xi.
После подстановки xiэ в уравнение (3.13), оно будет представлено в виде
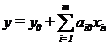 , (3.15)
, (3.15)
где ai0=ai∆xi.
Задачей факторного анализа является рациональное планирование экспериментальных исследований изучаемого объекта, позволяющее по их результатам наименее трудоемким путем определить коэффициенты a1, a2,…am уравнения линейной регрессии (3.13), моделирующего данный объект. Коэффициенты определяются таким образом, чтобы расчетные значения y, полученные по формуле (3.15), были равны экспериментальным значениям y, полученным при тех же значениях xiэ. Если будут проведены n циклов экспериментального определения значений y при различных наборах значений входных параметров (факторов) xi, то для определения параметров ai можно будет составить n уравнений вида
 ,
,  , (3.16)
, (3.16)
где yj - значение y, полученное в j –том эксперименте;
xiэj- относительное значение xi в j-том эксперименте.
В матричной форме эта система уравнений может быть представлена в виде:
Y=XэA0, (3.16’)
где Y– матрица-столбец экспериментальных значений y с числом элементов, равным n;
Xэ– матрица входных воздействий размером n×m;
A0– матрица-столбец коэффициентов ai0 с числом элементов, равным m.
Значения xi при проведении экспериментальных исследований варьируют таким образом, чтобы решение системы уравнений (3.16) относительно коэффициентов ai0 можно было представить в виде:
 , (3.17)
, (3.17)
где n – количество опытов по определению значений yi.
Для этого эксперименты проводят в следующем порядке:
· в каждом эксперименте полагают либо xi=ximax, либо xi=ximin, с тем чтобы получать всегда xiэ=1, либо xiэ=-1, для всех варьируемых факторов (условие нормированности);
· сумма всех экспериментальных значений каждого фактора xiэ в серии из n экспериментов должна быть равна нулю, т.е. должно быть
 ,
,  , (условие симметричности)
, (условие симметричности)
· сумма всех произведений  в серии из n экспериментов должна быть равна нулю (условие ортогональности).
в серии из n экспериментов должна быть равна нулю (условие ортогональности).
Значения ximax и ximin выбираются в зависимости от целей линеаризации параметра y. Чем ближе значение ximin к ximax, тем точнее аппроксимация функции y в области значений xi от ximax до ximin, но тем сложнее ограничивать разброс экспериментальных значений параметров в пределах, обеспечивающих заданную точность.
Если следовать рассмотренному порядку экспериментальных исследований, то окажется, что в ходе эксперимента каждый параметр (фактор) будет принимать только два значения: ximax и ximin. И если варьируется m факторов, то максимальное количество различных вариантов в одном цикле экспериментальных исследований составит 2m. Если в экспериментальном цикле реализуются все 2m вариантов, то такой эксперимент называют полнофакторным. Полнофакторный эксперимент всегда удовлетворяет условиям нормированности, симметричности и ортогональности. Он также обеспечивает максимальною точность расчетов. Однако, если желательно уменьшить объем эксперимента, то можно применить дробнофакторный эксперимент, когда в цикл экспериментальных исследований входят не все возможные варианты сочетаний факторов, но условия нормированности, симметричности и ортогональности все же выполняются.
Пример 3.2. Аппроксимировать зависимость объемной производительности J токарного станка от глубины резания tp и подачи на оборот s при постоянной скорости резания уравнением регрессии вида
 . (3.18)
. (3.18)

Рис.3.3. График производительности токарного станка
Экспериментальные усредненные зависимости tp при различных значениях параметра J приведены на рис.3.3. Пределы изменения глубины резания полагаем от tpmin=3 мм до tpmax=5 мм, а подачи на оборот – от smin=0,6 мм/об до smax=0,8 мм/об. Область определения функции J (tp,s) показана на рис.3.3 в виде прямоугольника a,b,c,d.
Усредненность кривых tp(s) позволяет полагать:
 ,
,  ;
;
 ,
,  .
.
Кроме того, полагаем:
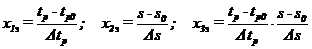 ,
,
что позволяет искать выражение (3.18) в форме линейной регрессии:
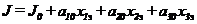 (3.19)
(3.19)
в соответствии с выражениями (3.15) и (3.16), где полагаем y=J. В рассматриваемом случае m=3, что ведет к полнофакторному эксперименту для определения значений a10, a20 и a30 в объеме восьми опытов. С целью уменьшения объема эксперимента ограничимся четырьмя опытами (n=4), проведенными в порядке, указанном в таблице 3.2.
Таблица 3.2

Значения x1э и x2э равны +1 при максимальных значениях tp и s и –1 - при минимальных значениях tp и s. Значения x3э равны произведению значений x1э и x2э. Экспериментальные значения J, соответствующие принятым значениям x1э, x2э и x3э, определены по точкам a, b, d и c на рис. 3.3. Как видно в таблице 3.2, дробнофакторный эксперимент, отображенный в ней, соответствует требованиям нормированности, симметричности и ортогональности. Поэтому, согласно (3.17), вычисляем:
 ;
;
аналогично получим a20=35 и a30=7,5. Кроме того, согласно (3.10) получим:
 ,
,
после чего выражение (3.19) будет представлено в виде:
 .
.
Последнее выражение приводится к виду (3.18) в такой форме:
 ,
,
так как a0=0.
Получение аналитического выражения J (tp,s) было обеспечено наличием усредненных экспериментальных зависимостей tp(s), приведенных на рис. 3.3. Определение зависимостей такого рода в условиях разброса экспериментальных данных требует применения регрессионного анализа в соответствии с выражениями (3.7) и (3.8), причем необходимо, чтобы объем и число повторений эксперимента обеспечивали нужный уровень достоверности модели.
Контрольные вопросы к главе 3
1. Что такое алгоритм функционирования, или модель ТО?
2. В чем состоит декомпозиция алгоритма ТО?
3. Как оценить эффективность построенной модели ТО?
4. В каком порядке производится построение аналитической модели ТО? Приведите пример типового звена ТО.
5. В чем отличие односвязных и многосвязных моделей ТО?
6. Приведите пример записи уравнений многосвязной линейной системы с перекрестными связями.
7. В каком порядке строится модель технологического цикла с помощью таблиц истинности?
8. Как реализуются последовательностные модели в виде циклограмм?
9. Как составляются граф-схемы технологического цикла?
10. В чем состоит экспериментальная идентификация ТО? Каковы ее трудности?
11. В чем состоит регрессионный анализ при экспериментальном исследовании параметров ТО?
12. Как используется уравнение линейной регрессии при экспериментальной идентификации ТО? Приведите пример.
13. Как записывается уравнение линейной регрессии многомерного (многосвязного) объекта?
14. В каком порядке производится факторный анализ многомерного объекта?
15. Как производится полнофакторный эксперимент? Приведите пример.
16. Разберите пример неполнофакторного эксперимента при определении зависимости объемной производительности токарного станка от глубины резания и подачи.
Дата добавления: 2018-04-04; просмотров: 699; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
