Функциональный анализ и интегральные уравнения
1. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа: Учебное пособие. М.: Наука.– 1981.– 542 с.
2. Антоневич А.Б., Радыно Я.В. Функциональный анализ и интегральные уравнения. Мн.:БГУ. – 2003. – 430 с.
3. Садовничий В.А. Теория операторов: Учебное пособие. М.: Изд-во Моск. Ун-та.– 1979.– 296 с.
4. Миротин А.Р. Функциональный анализ: мера и интеграл (допущено МО РБ в качестве учебного пособия для университетов) / М. : Книжный дом «ЛИБРОКОМ», 2012. – 160 c.
Теория функций комплексного переменного
1. Привалов И.И. Введение в теорию комплексного переменного: Учебн. М.: Наука, 1984, 43 с.
2. Маркушевич А.И. Краткий курс теории аналитических функций: Учебное пособие. М.: Наука, 1978, 387 с.
3. Шабат Б.В. Введение в комплексный анализ: Учебник, в 2-х ч. 2-е изд., переработанное и дополн. М.: Наука, 1976.
4. Евграфов М.А. Аналитические функции: Учебник. М., Наука, 1968, 471 с.
Теоретическая механика
1. Бухгольц, Н.Н. Основной курс теоретической механики: В 2-х ч. [Текст] / Н.Н.Бухгольц – М.: Наука, 1972.
2. Тарг, С.М. Краткий курс теоретической механики [Текст] / С.М.Тарг – М.: Наука, 1976.
3. Яблонский, А.А. Курс теоретической механики, ч. 1, 2. [Текст] / А.А.Яблонский – М.: Наука, 1971.
Алгебра и теория чисел. Аналитическая геометрия
1. Монахов В.С., Бузланов А.В. Алгебра и теория чисел : Практикум : учебное пособие. В 2-х частях. Ч.1. – Мн.: Изд. центр БГУ, 2007 г.
2. Милованов М.В., Тышкевич Р.И., Феденко А.С. Алгебра и аналитическая геометрия. – Мн.: Амалфея, 2001 г.
3. Виноградов И.М. Основы теории чисел. – М.: Наука, 1972 г.
4. Дубровин Б.А., Новиков С.П., Фоменко А.Г. Современная геометрия. – М.: Наука, 1979 г.
Дифференциальная геометрия и топология
1. Кононов С.Г., Прасолов А.В., Тимохович В.Л., Тралле А.Е., Феденко А.С. Топология. – Минск, “Вышэйшая школа”, 1990.
5. Феденко А.С., Фоменко А.Т. Курс дифференциальной геометрии. :МГУ, 1980.
2. Мищенко А.С., Фоменко А.Т. Курс дифференциальной геометрии и топологии. – М.: МГУ, 1980.
3. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа : Учебное пособие, М.: Наука, 1981, 542 с.
Дифференциальные уравнения
1. Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений. Минск: Вышэйшая школа, 1974.
2. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М.: 1984.
Уравнения математической физики
1. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1977.
2. Бицадзе А.В. Уравнения математической физики. М.: Наука, 1982.
3. Петровский И.Г. Лекции об уравнениях с частными производными. М.: Л.1950.
Теория вероятностей и математическая статистика
1. Гнеденко Б.В. Курс теории вероятностей. М.: Наука, 1969.
2. Крамер Г. Математические методы статистики. М.: Мир, 1975.
Методы вычислений и вычислительный практикум
1. Бахвалов Н.С. Численные методы. М.Наука, 1975.
2. Березин Н.С., Жидков Н.П. Методы вычислений. 1 и 2-й том. М.Наука, 1966.
3. Демидович Б.П., Марон И.А. Основы вычислительной математики.- М.: Наука, 1970.
Методика преподавания математики и информатики
1. Бочкин А.И. Методика преподавания информатики. – Мн.: Выш.шк., 1998. – 431 с.
2. Быдакоров Ю.А. и др. Информатика: Учебное пособие для 8-го (9-го) кл. общеобразовательных школ. – Мн.: Народная асвета, 2000(2001). – 191 с. (230 с.).
Методы оптимизации
1. Габасов Р., Кириллова Ф.М. Методы оптимизации. Минск,1981.
ПЕРЕЧЕНЬ ЗАДАЧ
Математический анализ
1. Найти предел 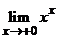 .
.
2. Найти пределы 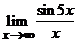 ,
, 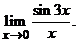
3. Найти точки разрыва функции  , установить их род и указать скачки в точках разрыва первого рода, если
, установить их род и указать скачки в точках разрыва первого рода, если
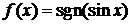 .
.
4. Является ли функция 
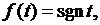
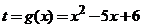 непрерывной на
непрерывной на 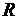 ? Дифференцируемой на
? Дифференцируемой на 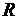 ? Найти ее производную в тех точках, где производная существует.
? Найти ее производную в тех точках, где производная существует.
5. Проведя исследование, построить график функции
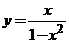 .
.
6. Вычислить следующие интегралы:
а) 
 б)
б) 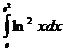 .
.
7. Найти 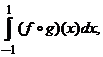 где
где 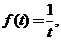

8. Вычислить 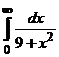 .
.
9. Найти площадь фигуры, ограниченной кривыми
y = 3x – x2 , x + y = 0.
10. Исследовать сходимость интеграла
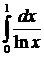
11. Найти 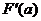 , если
, если
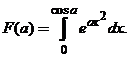
12. Найти: 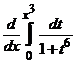 .
.
13. Исследовать на сходимость 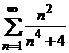 .
.
14. Исследовать на сходимость ряд
 .
.
15. Исследовать на сходимость 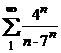 .
.
16. Найти область сходимости функционального ряда  его сумму и исследовать эту сумму на непрерывность
его сумму и исследовать эту сумму на непрерывность
17. Исследовать на равномерную сходимость ряд в указанном промежутке
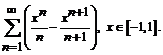
18. Написать ряд Фурье функции
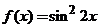 на отрезке
на отрезке 

19. Найти 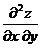 , если
, если 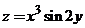 .
.
20. Найти дифференциал 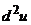 , если u = x3 + y3 + 3xy(x - y)
, если u = x3 + y3 + 3xy(x - y)
21. Изменить порядок интегрирования в повторном интеграле
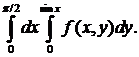
22. Вычислить 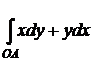 , где О – начало координат и A (1,4), по следующим кривым:
, где О – начало координат и A (1,4), по следующим кривым:
а) ОА - отрезок прямой линии;
б) ОА - парабола, ось которой есть OY;
в) ОА - ломаная линия, состоящая из отрезка ОВ оси ОХ и отрезка ВА, параллельного оси OY.
23. Применяя формулу Грина, вычислить криволинейный интеграл
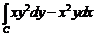 , где
, где 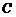 – окружность с уравнением x2 + y2 = 1.
– окружность с уравнением x2 + y2 = 1.
24. Вычислить пределы:
а) 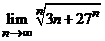 ; б)
; б) 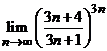 .
.
25. Существуют ли такие числа a и b, при которых функция
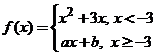
всюду дифференцируема?
26. Исследовать на дифференцируемость функцию

Дата добавления: 2018-04-04; просмотров: 492; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
