Для студентов заочной формы обучения
Контрольная работа №1
1 - 10. Даны векторы а (а1; а2; а3), b (b1; b2; b3), с (с1; с2; с3) и d (d1; d2; d3) в некотором базисе. Показать, что векторы а, b, c образуют базис, и найти координаты вектора d в этом базисе.
1. а(1;2;3), b(-1;3;2), с(7;-3;5), d(6;10;17).
2. а(4;7;8), b(9;1;3), с(2;-4;1), d(1;-13;-13).
3. а(8;2;3), b(4;6;10), с(3;-2;1), d(7;4;11).
4. а(10;3;1), b(1;4;2), с(3;9;2), d(19;30;7).
5. а(2;4;1), b(1;3;6), с(5;3;1), d(24;20;6).
6. а(1;7;3), b(3;4;2), с(4;8;5), d(7;32;14).
7. а(1;-2;3), b(4;7;2), с(6;4;2), d(14;18;6).
8. а(1;4;3), b(6;8;5), с(3;1;4), d(21;18;33).
9. а(2;7;3), b(3;1;8), c (2;-7;4), d (16;14;27).
10. а (7;2;1), b(4;3;5), с(3;4;-2), d(2;-5;-13).
11 - 20. Даны координаты вершин пирамиды А1А2А3А4. Найти 1) длину ребра А1А2; 2) угол между ребром А1А2 и А1А4; 3) угол между ребрами А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5) объем пирамиды; 6) уравнение прямой А1А2; 7) уравнение плоскости А1А2А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
11. А1 (4;2;5), А2 (0;7;2), А3 (0;2;7), А4 (1;5;0).
12.А1 (4;4;10), А2 (4;10;2), А3 (2;8;4), А4 (9;6;4).
13.А1 (4;6;5), А2 (6;9;4), А3 (2;10;10), А4 (7;5;9).
14.А1 (3;5;4), А2 (8;7;4), А3 (5;10;4), А4 (4;7;8).
15.А1 (10;6;6), А2 (-2;8;2), А3 (6;8;9), А4 (7;10;3).
16.А1 (1;8;2), А2 (5;2;6), А3 (5;7;4), А4 (4;10;9).
17.А1 (6;6;5), А2 (4;9;5), А3 (4;6;11), А4 (6;9;3).
18.А1 (7;2;2), А2 (5;7;7), А3 (5;3;1), А4 (2;3;7).
19.А1 (8;6;4), А2 (10;5;5), А3 (5;6;8), А4 (8;10;7).
20.А1 (7;7;3), А2 (6;5;8), А3 (3;5;8), А4 (8;4;1).
21.Уравнение одной из сторон квадрата х + 3у – 5 = 0. Составить уравнения трех остальных сторон квадрата, если (-1;0) – точка пересечения его диагоналей.
|
|
|
22.Даны уравнения одной из сторон ромба х - 3у + 10 = 0 и одной из его диагоналей х + 4у – 4 = 0; диагонали ромба пересекаются в точке (0, 1). Найти уравнения остальных сторон ромба.
23.Уравнения двух сторон параллелограмма х + 2у + 2 = 0 и х + у = 0, а уравнение одной из его диагоналей х – 2 = 0. Найти координаты вершин параллелограмма.
24.Даны две вершины А(-3;3) и В(5;-1) и точка D(4;3) пересечения высот треугольника. Составить уравнения его сторон.
25.Даны вершины А(-3;-2), В(4;-1), С(1;3) трапеции АВСD (AD  ВС). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции.
ВС). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции.
26.Даны уравнения двух сторон треугольника 5х - 4у + 15 = 0 и 4х + у – 9 = 0. Его медианы пересекаются в точке (0;2). Составить уравнение третьей стороны треугольника.
27.Даны две вершины А(2;-2) и В(3;-1) и точка Р(1;0) пересечения медиан треугольника АВС. Составить уравнение высоты треугольника, проведенной через третью вершину С.
28.Даны уравнения двух высот треугольника х + у = 4 и у = 2х и одна из его вершин А(0;2). Составить уравнения сторон треугольника.
29.Даны уравнения двух медиан треугольника х - 2у + 1 = 0 и у – 1 = 0 и одна из его вершин (1;3). Составить уравнения его сторон.
|
|
|
30.Две стороны треугольника заданы уравнениями 5х - 2у – 8 = 0 и 3х - 2у – 8 = 0, а середина третьей стороны совпадает с началом координат. Составить уравнение этой стороны.
31.Составить уравнение линии, расстояние каждой точки которой от начала координат и от точки А(5;0) относятся как 2:1.
32. Составить уравнение линии, расстояние каждой точки которой от точки А(-1;0) вдвое меньше расстояния ее от прямой х = - 4.
33.Составить уравнение линии, расстояния каждой точки которой от точки А(2;0) и от прямой 5х + 8 = 0 относятся как 5 : 4.
34.Составить уравнение линии, каждая точка которой находится вдвое дальше от точки А(4;0), чем от точки В(1;0).
35.Составить уравнение линии, расстояния каждой точки которой от точки А(2;0) и от прямой 2х + 5 = 0 относятся как 4 : 5.
36.Составить уравнение линии, расстояние каждой точки которой от точки А(3;0) вдвое меньше расстояния от точки В(26;0).
37.Составить уравнение линии, каждая точка которой одинаково удалена от точки А(0;2) и от прямой у – 4 = 0.
38.Составить уравнение линии, каждая точка которой равноотстоит от оси ординат и от окружности х2 + у2 = 4х.
39.Составить уравнение линии, каждая точка которой равноудалена от точки А(2;6) и о прямой у + 2 = 0.
|
|
|
40.Составить уравнение линии, каждая точка которой отстоит от точки А(-4;0) втрое дальше, чем от начала координат.
41 – 50. Линия задана уравнением r = r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ = 0 до φ = 2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой ситеме координат, у которой начало координат совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
41. 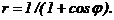
43. 
45. 
47. 
49. 
42. 
44. 
46. 
48. 
50. 
51 - 60. Дана система линейных уравнений:

Доказать ее совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.
51.  52.
52. 
53.  54.
54. 
55.  56.
56. 
57.  58.
58. 
59. 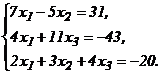 60.
60. 
61 - 80. Решить систему трех уравнений с тремя неизвестными при помощи определителей.
61.  62.
62. 
63. 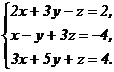 64.
64. 
|
|
|
65. 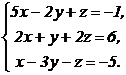 66.
66. 
67.  68.
68. 
69.  70.
70. 
71.  72.
72. 
73.  74.
74. 
75.  76.
76. 
77.  78.
78. 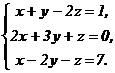
79.  80.
80. 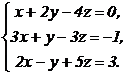
Контрольная работа №2
81 - 90. Дано комплексное число а. Требуется:1) записать число а в алгебраической и тригонометрической формах; 2) найти все корни уравнения z3 + а = 0.
81.  . 82.
. 82.  .
.
83.  . 84.
. 84. 
85.  . 86.
. 86. 
87.  . 88.
. 88.  .
.
89.  . 90.
. 90. 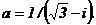 .
.
91 - 95. Построить график функции у = Аsin(ax+b) преобразованием графика функции у = sin x.
91. 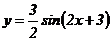 .
.
92.  .
.
93.  .
.
94.  .
.
95.  .
.
96 - 100. Построить график функции y = A cos(ax+b) преобразованием графика функции y = cos x.
96.  .
.
97.  .
.
98. 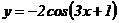 .
.
99. 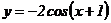 .
.
100.  .
.
101 - 120. Найти пределы функций, не пользуясь правилом Лопиталя.
| 101. | а) 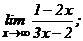
| б) 
|
в) 
| г) 
| |
| 102. | а) 
| б) 
|
в) 
| г) 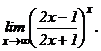
| |
| 103. | а) 
| б) 
|
в) 
| г) 
| |
| 104. | а) 
| б) 
|
в) 
| г) 
| |
| 105. | а) 
| б) 
|
в) 
| г) 
| |
| 106. | а) 
| б) 
|
в) 
| г) 
| |
| 107. | а) 
| б) 
|
в) 
| г) 
| |
| 108. | а) 
| б) 
|
в) 
| г) 
| |
| 109. | а) 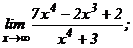
| б) 
|
в) 
| г) 
| |
| 110. | а) 
| б) 
|
в) 
| г) 
| |
| 111. | а) 
| б) 
|
в) 
| г) 
| |
| 112. | а) 
| б) 
|
в) 
| г) 
| |
| 113. | а) 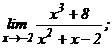
| б) 
|
в) 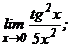
| г) 
| |
| 114. | а) 
| б) 
|
в) 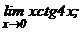
| г) 
| |
| 115. | а) 
| б) 
|
в) 
| г) 
| |
| 116. | а) 
| б) 
|
в) 
| г) 
| |
| 117. | а) 
| б) 
|
в) 
| г) 
| |
| 118. | а) 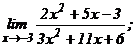
| б) 
|
в) 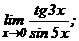
| г) 
| |
| 119. | а) 
| б) 
|
в) 
| г) 
| |
| 120. | а) 
| б) 
|
в) 
| г) 
|
121 - 130. Задана функция y = f(x) и два значения аргумента х1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
121. f(x)=91/(2-x), x1=0, x2=2.
123. f(x)=121/x, x1=0, x2=2.
125. f(x)=81/(5-x), x1=3, x2=5.
127. f(x)=141/(6-x), x1=4, x2=6.
129. f(x)=111/(4+x), x1=-4, x2=-2.
122. f(x)=41/(3-x), x1=1, x2=3.
124. f(x)=31/(4-x), x1=2, x2=4.
126. f(x)=101/(7-x), x1=5, x2=7.
128. f(x)=151/(8-x), x1=6, x2=8.
130. f(x)=131/(5+x), x1=-5, x2=-3.
В задачах 131 - 140 даны функции y = f(x) и значения аргумента х1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной при данных значениях аргумента; 2) найти односторонние пределы в точках разрыва; 3)построить график данной функции.
131. 
133. 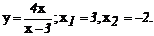
135. 
137. 
139. 
132. 
134 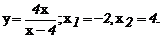
136. 
138. 
140. 
В задачах 141 - 150 функция у задана различными аналитическими выражениями для различных областей изменения аргумента х. Требуется: 1) найти точки разрыва функции, если они существуют; 2) найти односторонние пределы и скачок функции в точках разрыва; 3) сделать чертеж.
| 141. | 
| 146. | 
|
| 142. | 
| 147. | 
|
| 143. | 
| 148. | 
|
| 144. | 
| 149. | 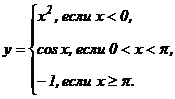
|
| 145. | 
| 150. | 
|
151 - 160. Задана функция y = f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
151. 

152. 

153. 

154. 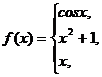

155. 

156. 
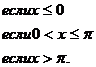
157. 

158. 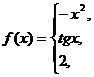

159. 

160. 

Контрольная работа №3
161 - 170. Найти производные 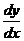 данных функций.
данных функций.
| 161. | 
| 162. | 
|
| 163. | 
| 164. | 
|
| 165. | 
| 166. | 
|
| 167. | 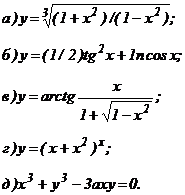
| 168. | 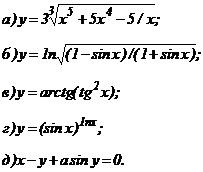
|
| 169. | 
| 170. | 
|
171 - 180. Найти  и
и 
171. 


172. 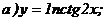


173. 


174. 


175. 


176. 


177. 

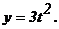
178. 
 ,
, 
179. 

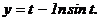
180. 
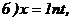
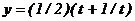 .
.
181 - 190. Найти наибольшее и наименьшее значения функции у = f(x) на отрезке 
181. 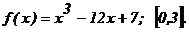
182. 
183. 
184. 
185. 
186. 
187. 
188. 
189. 
190. 
191 - 210. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.
191. у = 4х/(4+х2) 192. y = (x2-1)/(x2 +1)
193. y = (x2+1)/(x2-1) 194. y = x2/(x-1)
195. y = x3/(x2+1) 196. y = (4x3+5)/x
197. y = (x2-5)/(x-3) 198. y = x4/(x3-1)
199. y = 4x3/(x3-1) 200. y = (2-4x2)/(1-4x2)
201. y = (1nx)/  202. y = x
202. y = x 
203. y =  204. y = x2-21nx
204. y = x2-21nx
205. y = 1n (x2-4) 206. y = e1/(2-x)
207. y = 1n (x2+1) 208. y = (2+x2) 
209. y = 1n (9-x2) 210. y = (x-1)e3x+1.
211. Дана функция z = y/(x2- y2)5. Показать, что 
212. Дана функция z = y2/(3x)+arcsin(xy). Показать, что 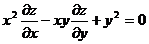
213. Дана функция z = 1n(x2+y2+2x+1). Показать, что 
214. Дана функция z = exy. Показать, что 
215. Дана функция z = 1n(x+e-y). Показать, что 
216. Дана функция z = x/y. Показать, что 
217. Дана функция z = xy. Показать, что 
218. Дана функция z = xey/x. Показать, что 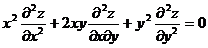
219. Дана функция z = sin(x+ay). Показать, что 
220. Дана функция z = cosy+(y - x)siny. Показать, что 
221 - 230. Дана функция z = f(x,y) и две точки А(х0, у0) и В(х1, у1). Требуется: вычислить значение z1 функции в точке В; 2) вычислить приближенное значение  функции в точке В, исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом, и оценить в процентах относительную погрешность, возникающую при замене приращения функции ее дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке С(х0, у0, z0).
функции в точке В, исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом, и оценить в процентах относительную погрешность, возникающую при замене приращения функции ее дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке С(х0, у0, z0).
221. z = x2+xy+y2; А(1;2), В(1,02;96)
222. z = 3x2-xy+x+y; А(1;3), В(1,06;2,92)
223. z = x2+3xy-6y; А(4;1), В(3,96;1,03)
224. z = x2-y2+6x+3y; А(2;3), В(2,02;2,97)
225. z = x2+2xy+3y2 ; А(2;1), В(1,96;1,04)
226. z = x2+y2+2x+y-1; А(2;4), В(1,98;3,91)
227. z = 3x2+2y2-xy; А(-1;3), В(-0,98;2,97)
228. z = x2-y2+5x+4y; А(3;3), В(3,02;2,98)
229. z = 2xy+3y2-5x; А(3;4), В(3,04;3,95)
230. z = xy+2y2-2x; А(1;2), В(0,97;2,03).
231 - 240. Найти наименьшее и наибольшее значения функции z = f(x,y) в замкнутой области D, заданной системой неравенств. Сделать чертеж.
231. z = x2+y2-9xy+27; 
 .
.
232. z = x2+2y2+1; 
 .
.
233. z = 3-2x2-xy-y2; 
 .
.
234. z = x2+3y2+x-y; 

235. z = x2+2xy+2y2; 
 .
.
236. z = 5x2-3xy+y2+4; 

237. z = 10+2xy-x2; 
238. z = x2+2xy-y2+4x; 
 .
.
239. z = x2+xy-2; 
240. z = x2+xy; 
 .
.
241 - 250. Даны функции z = z(x,y), точка А(х0,у0) и вектор а. Найти; 1) grad z в точке А; 2)производную в точке А по направлению вектора а.
241. z = x2+xy+y2; А(1;1), а = 2i-j.
242. z = 2x2+3xy+y2; А(2;1), a = 3i-4j.
243. z = 1n(5x2+3y2); А(1;1), a = 3i+2j.
244. z = 1n(5x2+4y2); А(1;1), a = 2i-j.
245. z = 5x2+6xy; А(2;1), a = i+2j.
246. z = arctg(xy2); А(2;3), a = 4i-3j.
247. z = arcsin (x2/y); А(1;2), a = 5i-12j.
248. z = 1n(3x2+4y2); А(1;3), a = 2i-j.
249. z = 3x4+2x2y3; А(-1;2), a = 4i-3j.
250. z = 3x2y2+5y2x; А(1;1), a = 2i+j.
251 - 260. Экспериментально получены пять значений искомой функции y = f(x) при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию y = f(x) в виде у = ах + b.
251.
| х | 1 | 2 | 3 | 4 | 5 |
| у | 4,3 | 5,3 | 3,8 | 1,8 | 2,3 |
252.
| х | 1 | 2 | 3 | 4 | 5 |
| у | 4,5 | 5,5 | 4,0 | 2,0 | 2,5 |
253.
| х | 1 | 2 | 3 | 4 | 5 |
| у | 4,7 | 5,7 | 4,2 | 2,2 | 2,7 |
254.
| х | 1 | 2 | 3 | 4 | 5 |
| у | 4,9 | 5,9 | 4,4 | 2,4 | 2,9 |
255.
| х | 1 | 2 | 3 | 4 | 5 |
| у | 5,1 | 6,1 | 4,6 | 2,6 | 3,1 |
256.
| х | 1 | 2 | 3 | 4 | 5 |
| у | 3,9 | 4,9 | 3,4 | 1,4 | 1,9 |
257.
| х | 1 | 2 | 3 | 4 | 5 |
| у | 5,2 | 6,2 | 4,7 | 2,7 | 3,2 |
258.
| х | 1 | 2 | 3 | 4 | 5 |
| у | 5,5 | 6,5 | 5,0 | 3,0 | 3,5 |
259.
| х | 1 | 2 | 3 | 4 | 5 |
| у | 5,7 | 6,7 | 5,2 | 3,2 | 3,7 |
260.
| х | 1 | 2 | 3 | 4 | 5 |
| у | 5,9 | 6,9 | 5,4 | 3,4 | 3,9 |
Контрольная работа №4
261 - 270. Найти неопределенные интегралы. В двух первых примерах а) и б) проверить результаты дифференцированием.
261. 



262. 


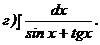
263. 



264. 
 ;
;


265. 
 ;
;

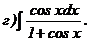
266. 


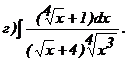
267. 

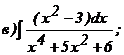
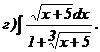
268. 



269. 



270. 



271 - 280. Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
271. 
273. 
272. 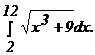
274. 
275. 
277. 
279. 
276. 
278. 
280. 
281 - 290. Вычислить несобственный интеграл или доказать его расходимость.
281. 
283. 
285. 
287. 
289. 
282. 
284. 
286. 
288. 
290. 
291. Вычислить площадь фигуры, ограниченной параболой у = 3х2 + 1 и прямой у = 3х + 7.
292. Вычислить площадь фигуры, ограниченной одной аркой циклоды х = а(t - sin t), y = a(1 - cos t),  и осью Ох.
и осью Ох.
293. Вычислить площадь фигуры, ограниченной кардиоидой r = 3(1 + cos φ).
294. Вычислить площадь фигуры, ограниченной четырехлепестковой розой r = 4sin 2φ.
295. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболами у = х2 и у =  .
.
296. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной полуэллипсом у =  , параболой х =
, параболой х =  и осью Оу.
и осью Оу.
297. Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной кривыми у = 2/(1 + х2)4 и у = х2.
298. Вычислить длину дуги полукубической параболы у =  от точки А (2;0) до точки В (6;8).
от точки А (2;0) до точки В (6;8).
299. Вычислить длину кардиоиды r = 3(1 - cosφ).
300. Вычислить длину одной арки циклоиды х = 3(t - sint), y = 3(1 - cost),  .
.
301 - 320. Найти общее решение дифференциального уравнения.
301. 
302. 
303. 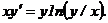
304. 
305. 
306. 
307. 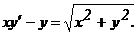
308. 
309. 
310. 
311. 
312. 
313. 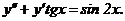
314. 
315. 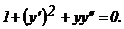
316. 
317. 
318. 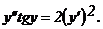
319. 
320. 
В задачах 321 - 330 даны дифференциальные уравнения второго порядка, допускающие понижение порядка. Найти частное решение, удовлетворяющее указанным начальным условиям.
321. у΄΄- еуу΄= 0, у(0) = 0, у΄(0) = 1.
322. у΄у΄΄= 2у, у(0) = 0, у΄(0) = 0.
323. уу΄΄= (у΄)2, у(0) = 1, у΄(0) = 3.
324. у3у΄΄= 3, у(1) = 1, у΄(1) = 1.
325. у΄΄-12у2= 0, у(0) =1/2, у΄(0) = 1.
326. 2у΄΄=е4у, у(0) = 0, у΄(0) = ½.
327. (у – 2)у΄΄ = 2(у΄)2, у(0) = 3, у΄(0) = 1.
328. 2уу΄΄= 3 + (у΄)2, у(1) = 1, у΄(1) = 1.
329. у΄΄=  у(2) = 0, у΄(2) = 2.
у(2) = 0, у΄(2) = 2.
330. (у + 1)2у΄΄= (у΄)3, у΄(0) = 1.
331 - 340. Найти частное решение дифференциального уравнения  , удовлетворяющее начальным условиям у(0)=у0,
, удовлетворяющее начальным условиям у(0)=у0, 
331. 

332. 

333. 

334. 

335. 
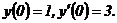
336. 

337. 

338. 

339. 

340. 

В задачах 441 - 450 даны линейные неоднородные дифференциальные уравнения второго полрядка с постоянными коэффициентами. Найти частное решение, удовлетворяющее указанным начальным условиям.
441. y΄΄-2y΄-8y=16x2+2, y(0)=0, y΄(0)=5.
442. y΄΄+4y=3cos x, y(0)=1, y΄(0)=2.
443. y΄΄-y΄-2y=3e2x, y(0)=2, y΄(0)=5.
444. y΄΄-2y΄=2x+1, y(0)=1, y΄(0)=1.
445. y΄΄-2y΄+y=9e-2x+2x-4, y(0)=1, y΄(0)=1.
446. y΄΄-4y=4sin 2x, y(0)=2, y΄(0)=7.
447. y΄΄+y΄=3cos x – sin x, y(0)=0, y΄(0)=1.
448. y΄΄-y΄-6y=6x2-4x-3, y(0)=3, y΄(0)=5.
449. y΄΄-3y΄=3e3x, y(0)=2, y΄(0)=4.
450. y΄΄-4y΄+5y=5x – 4, y(0)=0, y΄(0)=3.
351 - 360. Дана система линейных дифференциальных уравнений с постоянными коэффициентами

Требуется найти общее решение системы.
351. 
353. 
355. 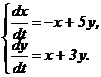
357. 
359. 
352. 
354. 
356. 
358. 
360. 
Контрольная работа №5
361. Вычислить площадь фигуры, ограниченной параболами 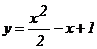 и
и  .
.
362. Вычислить площадь фигуры, ограниченной эллипсом x = acos t, y = bsint.
363. Вычислить площадь фигуры, ограниченной астроидой x = 4cos3t, y = 4sin3t.
364. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболой 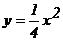 , х = 4 и осью Ох.
, х = 4 и осью Ох.
365. Найти объем тела, полученного вращением вокруг оси Оу фигуры, ограниченной гиперболой у = 6/х, осью Оу и прямыми у = 1 и у = 6.
366. Найти объем тела, полученного вращением вокруг оси Ох эллипса х = аcost, y = bsint.
367. Найти длину дуги кривой  от х1 = 0 до х2 = 12.
от х1 = 0 до х2 = 12.
368. Найти длину дуги кривой у = lnx от х1= ¾ до х2 = 2,4.
369. Найти длину одной арки циклоиды х = а(t - sint), y = a(1-cost).
370. Найти длину кардиоиды r = 2a(1-cosφ).
В задачах 371 - 380 вычислить объем тела, ограниченного указанными поверхностями. Данное тело и область интегрирования изобразить на чертеже.
371. 
372. 
373. 
374. 
375. 
376. 
377. 
378. 
379. 
380. 
381 - 390. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость хОу.
381. z = 0, z = x, у = 0, y = 4, x =  .
.
382. z = 0, z = 9 - y2, x2 + y2 = 9.
383. z = 0, z = 4 – x - y, x2 + y2 = 4.
384. z = 0, z = y2, x2 + y2 = 9.
385. z = 0, y + z = 2, x2 + y2 = 4.
386. z = 0, 4z = y2, 2x – y = 0, x + y = 9.
387. z = 0, x2 + y2 = z, x2 + y2 = 4.
388. z = 0, z = 1 - y2, x = y2, x = 2y2 + 1.
389. z = 0, z = 1 - x2, y = 0, y = 3 - x.
390. z = 0, z = 4  , x = 0, x + y = 4.
, x = 0, x + y = 4.
391. Вычислить криволинейный интеграл

вдоль дуги L окружности х = 5cos t, y =5sin t, обходя ее против хода часовой стрелки от точки А(5;0) до точки В(0;5). Сделать чертеж.
392. Вычислить криволинейный интеграл

вдоль ломаной L = OAB, где О(0;0), А(2;0), В(4;5). Сделать чертеж.
393. Вычислить криволинейный интеграл

вдоль границы L треугольника АВС, обходя ее против хода часовой стрелки, если А(1;0), В(1;1), С(0;1). Сделать чертеж.
394. Вычислить криволинейный интеграл

вдоль дуги L параболы у = х2 от точки А(-1;1) до точки В(1;1). Сделать чертеж.
395. Вычислить криволинейный интеграл

вдоль верхней половины L эллипса х = 3cos t, y = 2sin t  . Сделать чертеж.
. Сделать чертеж.
396. Вычислить криволинейный интеграл
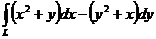
вдоль ломаной L = ABC, где А(1;2), В(1;5), С(3;5). Сделать чертеж.
397. Вычислить криволинейный интеграл

вдоль дуги L кривой у = е-х от точки А(0;1) до точки В(-1;е). Сделать чертеж.
398. Вычислить криволинейный интеграл
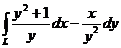
вдоль отрезка L = AB прямой от точки А(1;2) до точки В(2;4). Сделать чертеж.
399. Вычислить криволинейный интеграл

вдоль дуги L параболы у = 2х2 от точки А(0;0) до точки В(1;2). Сделать чертеж.
400. Вычислить криволинейный интеграл

вдоль дуги L кривой у =1n x от точки А(1;0) до точки В(е;1). Сделать чертеж.
В задачах 401 - 410 найти функцию U(x, y) по ее полному дифференциалу dU.
401. 
402. 
403. 
404. 
405. 
406. 
407. 
408. 
409. 
410. 
411 - 420. Исследовать сходимость числового ряда.
411. 
412. 
413. 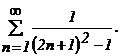
415. 
417. 
419. 
414. 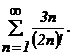
416. 
418. 
420. 
421 - 430. Найти интервал сходимости степенного ряда.
421.  422.
422. 
423.  424.
424. 
425. 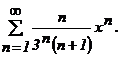 426.
426. 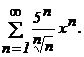
427.  428.
428. 
429. 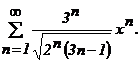 430.
430. 
431 - 440. Вычислить определенный интеграл  с точностью до 0,001, разложив подынтегральную функцию в ряд и затем проинтегрировав его почленно.
с точностью до 0,001, разложив подынтегральную функцию в ряд и затем проинтегрировав его почленно.
431. 
433. 
432. 
434. 
435. 
437. 
439. 
436. 
438. 
440. 
Контрольная работа №6
441 - 450. Методом Даламбера найти уравнение и = и(х, t) формы однородной бесконечной струны, определяемой волновым уравнением  , если в начальный момент tо = 0 форма струны и скорость точки струны с абсциссой х определяются соответственно заданными функциям
, если в начальный момент tо = 0 форма струны и скорость точки струны с абсциссой х определяются соответственно заданными функциям 
441. f(x)=x(2-x), F(x)=e-x.
442. f(x)=x2, F(x)= sin x.
443. f(x)=ex, F(x)=ωx.
444. f(x)=cos x, F(x)=ωx.
445. f(x)=sin x, F(x)=υ0.
446. f(x)=x, F(x)= cos x.
447. f(x)= sin x, F(x)= cos x.
448. f(x)=x(x-2), F(x)= ex .
449. f(x)= cos x, F(x)= υ0.
450. f(x)=e-x, F(x)= sin x.
451-460.Методом Фурье найти решение 
 уравнения теплопроводности
уравнения теплопроводности  , если в начальный момент времени
, если в начальный момент времени  температура стержня длины
температура стержня длины 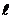 определяется заданной функцией
определяется заданной функцией  , а на границах стержня температура задается постоянной и равной, т.е.
, а на границах стержня температура задается постоянной и равной, т.е.  .
.
451. f(x)=x
452.f(x)=1
453.f(x)=x-1
454.f(x)=x+1
455.f(x)=2x-1
456.f(x)=2x+1
457.f(x)=1-3x
458.f(x)= 
459.f(x)= 
460.f(x)=1-2x
461 - 470. Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.
461.  ,
, 
462.  ,
, 
463.  ,
, 
464.  ,
, 
465.  ,
, 
466.  ,
, 
467.  ,
, 
468. 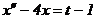 ,
, 
469.  ,
, 
470.  ,
, 
471 - 480. Методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее начальным условиям.
471.  x(0)=1, y(0)=0.
x(0)=1, y(0)=0.
472.  x(0)=1, y(0)=1, z(0)=1.
x(0)=1, y(0)=1, z(0)=1.
473.  x(0)=2, y(0)=3.
x(0)=2, y(0)=3.
474.  x(0)=2, y(0)=1/2, z(0)=5/2.
x(0)=2, y(0)=1/2, z(0)=5/2.
475.  x(0)=1, y(0)=1.
x(0)=1, y(0)=1.
476.  x(0)=2, y(0)=2, z(0)=-1.
x(0)=2, y(0)=2, z(0)=-1.
477.  x(0)=0, y(0)=0.
x(0)=0, y(0)=0.
478.  x(0)=1, y(0)=2, z(0)=3.
x(0)=1, y(0)=2, z(0)=3.
479.  x(0)=1, y(0)=-1.
x(0)=1, y(0)=-1.
480.  x(0)=1, y(0)=1.
x(0)=1, y(0)=1.
481. Студент знает 45 из 60 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятность того, что: а) студент знает все три вопроса; б) только два вопроса; в) только один вопрос экзаменационного билета.
482. В каждой из двух урн находятся 5 белых и 10 черных шаров. Из первой урны во вторую переложили неудачу один шар, а затем из второй урны вынули наугад один шар. Найти вероятность того, что вынутый шар окажется черным.
483. Три стрелка в одинаковых и независимых условиях производили по одному выстрелу по одной и той же целию Вероятность поражения цели первым стрелком равна 0,9, вторым – 0,8, третьим – 0,7. Найти вероятность того, что: а) только один из стрелков попадает в цель; б) только два стрелка попадут в цель; в) все три стрелка попадут в цель.
484. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,8. Найти вероятность того, что в 1600 испытаниях событие наступит 1200 раз.
485. Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равна 0,9, второе – 0,95, третье – 0,85. Найти вероятность того, что при аварии сработает: а) только одно устойство; б) только два устройства; в) все три устройства.
486. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,02. Найти вероятность того, что в 150 испытаниях событие наступит 5 раз.
487. В партии из 1000 изделий имеются 10 дефектных. Найти вероятность того, что среди 50 изделий, наудачу взятых из этой партии, ровно три окажутся дефектными.
488. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,8. Найти вероятность того, что в 125 испытаниях событие наступит не менее 75 и не более 90 раз.
489. На трех станках при одинаковых и независимых условиях изготовляют детали одного наименования. На первом станке изготовляют 10%, на втором – 30, на третьем – 60% всех деталей. Вероятность каждой детали быть бездефектной равна 0,7, если она изготовлена на первом станке, 0,8, - если на втором станке, и 0,9, - если на третьем станке. Найти вероятность того, что наугад взятая деталь окажется бездефектной.
490. Два брата входят в состав двух спортивных команд, состоящих из 12 человек каждая. В двух урнах имеются по 12 билетов с номерами от 1до 12. Члены каждой команды вынимают наудачу по одному билету из определенной урны (без возвращения). Найти вероятность того, что оба брата вытащат билет номер 6.
491 - 500. Задан закон распределения случайной величины X – размер деталей, выпускаемых заводом ( в первой строке таблицы даны возможные значения измеренной детали, а во второй строке указаны вероятности p этих возможных значений).
Найти: 1) математическое ожидание M(X); 2) дисперсию D(X); 3) среднее квадратическое отклонение  .
.
| 491. | X | 23 | 25 | 28 | 29 |
| P | 0.3 | 0.2 | 0.4 | 0.1 | |
| 492. | X | 17 | 21 | 25 | 27 |
| P | 0.2 | 0.4 | 0.3 | 0.1 | |
| 493. | X | 24 | 26 | 28 | 30 |
| P | 0.2 | 0.2 | 0.5 | 0.1 | |
| 494. | X | 12 | 16 | 19 | 21 |
| P | 0.1 | 0.5 | 0.3 | 0.1 | |
| 495. | X | 25 | 27 | 30 | 32 |
| P | 0.2 | 0.4 | 0.3 | 0.1 | |
| 496. | X | 30 | 32 | 35 | 40 |
| P | 0.1 | 0.5 | 0.2 | 0.2 | |
| 497. | X | 12 | 14 | 16 | 20 |
| P | 0.1 | 0.2 | 0.5 | 0.2 | |
| 498. | X | 21 | 25 | 28 | 31 |
| P | 0.1 | 0.4 | 0.2 | 0.3 | |
| 499. | X | 60 | 64 | 67 | 70 |
| P | 0.1 | 0.3 | 0.4 | 0.2 | |
| 500. | X | 45 | 47 | 50 | 52 |
| P | 0.2 | 0.4 | 0.3 | 0.1 | |
| 501. | X | 46 | 49 | 51 | 55 |
| P | 0,2 | 0,3 | 0,1 | 0,4 | |
| 502. | X | 18 | 22 | 23 | 26 |
| P | 0,2 | 0,3 | 0,4 | 0,1 | |
| 503. | X | 78 | 80 | 84 | 85 |
| P | 0,2 | 0,3 | 0,1 | 0,4 | |
| 504. | X | 37 | 41 | 43 | 45 |
| P | 0,2 | 0,1 | 0,5 | 0,2 | |
| 505. | X | 25 | 28 | 30 | 33 |
| P | 0,1 | 0,2 | 0,4 | 0,3 | |
| 506. | X | 56 | 58 | 60 | 64 |
| P | 0,2 | 0,3 | 0,4 | 0,1 | |
| 507. | X | 31 | 34 | 37 | 40 |
| P | 0,3 | 0,5 | 0,1 | 0,1 | |
| 508. | X | 17 | 20 | 23 | 27 |
| P | 0,1 | 0,4 | 0,3 | 0,2 | |
| 509. | X | 28 | 32 | 34 | 36 |
| P | 0,1 | 0,2 | 0,2 | 0,5 | |
| 510. | X | 35 | 39 | 42 | 46 |
| P | 0,1 | 0,3 | 0,2 | 0,4 | |
511 - 520. Найти доверительный интеграл для оценки математического ожидания а нормального распределения с надежностью 0,95 зная выборочную среднюю  , объем выборки n и среднее квадратическое отклонение σ.
, объем выборки n и среднее квадратическое отклонение σ.
511. 


512. 


513. 


514. 


515. 


516. 


517. 
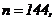
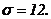
518. 


519. 


520. 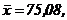


Дата добавления: 2018-04-04; просмотров: 364; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
