Метод решения задания с параметром с помощью нахождения области значений функции
Nbsp; МБОУ Покровская улусная многопрофильная гимназия МР Хангаласский улус РС (Я)
Методы решения заданий
С параметрами.
доклад учителя математики ПУМГ
Владимирова Михаила Даниловича
г. Покровск 2016 г.
Содержание
Введение……………………………………………………………………..3
Теоретические сведения
1.1. Полезные замечания о методах решения заданий с параметрами…4
1.2. Общие алгоритмы решения заданий с параметрами ……………….4
Способы решения заданий с параметрами
2.1. Графический метод…….………………………………………………5
2.2. Применение области значений функции …………………………...9
2.3. Применение четности или нечетности функции ……………………10
2.4. Геометрический метод ………………………………. ……………..11
2.5. Применение периодичности функций………………………………..13
2.6. Аналитический метод …………………………………………………14
2.7. Метод областей на координатной плоскости ……………………….15
Задачи для самостоятельного решения (с ответами) ……………………16
Заключение ………………………………………………………………….
|
|
|
Список использованной литературы ………………………………………17
Введение
На любых испытаниях и во время учебного процесса наибольшую сложность вызывают задачи с параметрами. Это объясняется двумя основными причинами. Во-первых, этой теме очень мало времени уделяется школьной программой. А вторая (основная) причина заключается в том, что это наиболее трудная тема как в логическом, так и техническом плане.
Основное содержание данного доклада составляют некоторые методы решения задач, содержащих параметры. Трудность в работе с задачами, содержащими параметр, заключается в большом разнообразии применяемых методов, необходимости особой аккуратности при решении и записи ответа. Трудности решения такого рода задач также вызваны тем, что в любом случае, даже при решении простейших уравнений или неравенств, содержащих параметры, приходится производить ветвление всех значений параметров на отдельные классы, при каждом из которых задача имеет решение. При этом следует четко и последовательно следить за сохранением равносильности решаемых уравнений или неравенств с учетом области определения выражений, входящих в уравнение или неравенство, а также учитывать выполнимость производимых операций.
|
|
|
Актуальность
Решение заданий с параметрами традиционно вызывает у учащихся непреодолимые трудности.
Из справки 2013 года:
К заданию С5 приступила только одна ученица, и только после систематических подготовок по решению таких заданий (0,1 % учащихся района). Для заданий с параметрами нужна большая систематизация методов решения таких заданий.
Объект исследования
Решение заданий с параметрами из ЕГЭ в блоке С (задание С5).
Предмет исследования
Решение заданий с параметрами разными методами. Систематизация этих методов.
В рамках данной работы рассмотрены типовые задачи ЕГЭ – С5, также их решение разными методами.
В своей работе я показал, как решаются задания с параметрами, систематизируя их по разным методам.
Итак, цель моей данной работы:
1. раскрыть содержание методов, рассказать основные формулы и свойства функций,
2. показать применение методов при решении конкретных задач,
3. решить сложные параметрические задачи с использованием разных методов.
Гипотеза
1. Через решение задач на нахождение параметров в разных условиях разными методами сделать систематизацию заданий с параметрами и научить школьников выбрать тот или иной способ решения задания этого блока.
|
|
|
2. Расширить представление о существовании разных методов при решении заданий с параметрами.
3. Применяя разные методы решения заданий с параметрами решить задания из ЕГЭ в блоке С (задание С5).
В задачах с параметром, кроме неизвестных величин, используются величины, численные значения которых не указаны конкретно, но считаются известными и удовлетворяющими каким-либо условиям. Например, значения параметра могут быть целыми, положительными и т.д. Будем рассматривать только действительные значения параметра и неизвестных.
Общее уравнение с одним неизвестным и одним параметром имеет вид F(x; a) = 0. При записи F(x; a) = 0 иногда смотрят на x как на параметр, а на a как на неизвестное. А можно рассматривать как уравнение с двумя равноправными переменными. На любое уравнение с несколькими переменными вида F(x; y; z) = 0 можно смотреть как на уравнение с параметрами. На самом деле, решая задачу с параметром, мы решаем много ≪похожих≫ задач. Если a заменить на конкретное a0, то получим уравнение без параметра: F(x; a0) = 0.
В течение многих лет в вариантах заданий ЕГЭ по математике предлагаются задания с параметрами. При решении задач с параметрами применяется много методов, из которых я остановлюсь на некоторых из них: нахождение области значений функции, использование свойств четности и нечетности функции, периодичности функции, геометрический и графический методы.
|
|
|
Графический метод.
Задача 1. Найдите все значения параметра а, при которых уравнение  имеет хотя бы один корень.
имеет хотя бы один корень.
Решение. Представим уравнение  в виде
в виде  и рассмотрим функции
и рассмотрим функции  . Так как
. Так как 
При 

При 
Построим схематические графики функций  .
.
Уравнение не имеет решения, если
24 1) 


18 2) 

y=g(x) y=f(x) 
Таким образом уравнение не имеет решения при
 .
.
Тогда уравнение имеет хотя бы один корень при
 .
.
Ответ: 
a 2 3 6
рис1
Задача 2. Найдите все значения а, при которых уравнение  имеет ровно два корня.
имеет ровно два корня.
Решение. При х =0 - 3 =0 неверно, поэтому х 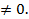 Тогда уравнение делим на х. Получим
Тогда уравнение делим на х. Получим 

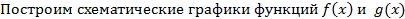 (cмотри рис 2).
(cмотри рис 2).
При а=2 уравнение имеет одно решение, при а=3 уравнение имеет три решения. Тогда два решения при  Ровно два решения если при х < 2 уравнение
Ровно два решения если при х < 2 уравнение  имеет одно решение. Пусть
имеет одно решение. Пусть  это решение. Производные в этой точке существуют и совпадают.
это решение. Производные в этой точке существуют и совпадают.  =2
=2  Имеем систему
Имеем систему 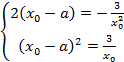



Ответ: при  ровно два корня.
ровно два корня.

0 2 3
Рис2
Задача 3. Найдите значения параметра а, при которых уравнение 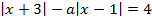 имеет два корня, и укажите значения корней.
имеет два корня, и укажите значения корней.
Решение. Представим уравнение в виде  Рассмотрим функции
Рассмотрим функции  Построим схематические графики этих функций.
Построим схематические графики этих функций.
a=2 при 
 бесконечно много решений. при
бесконечно много решений. при  a=
a=  одно решение х = 1.
одно решение х = 1.
при  два решения:
два решения:

Действительно, при 


Рис3 a = -0,5 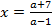 .
.
Ответ: при  имеет два корня
имеет два корня 
Задача 4. Найдите все значения параметра р, при каждом из которых уравнение 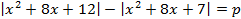 имеет более двух решений.
имеет более двух решений.
Решение. Представим уравнение в виде  и рассмотрим функции
и рассмотрим функции  Построим схематические графики этих функций.
Построим схематические графики этих функций. 


 (смотри рис4).
(смотри рис4).
При  бесконечно много корней
бесконечно много корней
При  нет корней
нет корней
При  четыре корня.
четыре корня.
Ответ: при 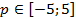 более двух решений
более двух решений
 9
9

 4
4
-7-6 -4 -2-1 x
Задача 5. Найдите наименьшее целое значение параметра а, при котором уравнение
 имеет ровно четыре решения.
имеет ровно четыре решения.
Решение. Рассмотрим функцию  и построим график этой функции.
и построим график этой функции.
Первый этап:  ; Второй этап:
; Второй этап: 
У у



3,5
Х х
-3,5
Уравнение имеет четыре решения при 
Наименьшее целое значение 
Ответ: 
Задача 6. Найдите все значения параметра а, при каждом из которых функция  имеет ровно три нуля функции.
имеет ровно три нуля функции.
Решение. Рассмотрим уравнение 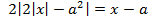 , которое должно иметь три решения. Рассмотрим функции
, которое должно иметь три решения. Рассмотрим функции  и построим схематические графики этих функций. Если
и построим схематические графики этих функций. Если  , то уравнение
, то уравнение  имеет одно решение, что не подходит условию задачи. Поэтому
имеет одно решение, что не подходит условию задачи. Поэтому  Графики функций смотрите на рис.6. Три решения получается, если графики данных функций при одном и том же а проходят через точки А(х;0) и В(0;у). В остальных случаях либо четыре решения, либо два решения, либо одно решение, либо нет решения. В случае точки А получаем:
Графики функций смотрите на рис.6. Три решения получается, если графики данных функций при одном и том же а проходят через точки А(х;0) и В(0;у). В остальных случаях либо четыре решения, либо два решения, либо одно решение, либо нет решения. В случае точки А получаем:  ,
,
 При
При  график функции
график функции  не пересекает график функции
не пересекает график функции  . Поэтому
. Поэтому  . Тогда
. Тогда 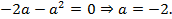
В случае точки B получаем: 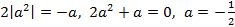 .
.


B
A

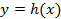
Ответ: 
Задача 7. Найдите все значения параметра а, при каждом из которых наименьшее значение функции  больше 2.
больше 2.
Решение. Наименьшее значение функции  Представим неравенство в виде
Представим неравенство в виде 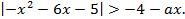 Построим графики функций
Построим графики функций
 ,
, 
B Для точки А имеем 
Для точки В имеем касательную к графику функции

Y=h(x)  . Уравнение касательной в точке
. Уравнение касательной в точке 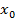
 . С учетом
. С учетом
графика 
`-a<12, a> - 12.
 Ответ:
Ответ: 
A
-5 -1
Y=h(x)
-4
Задача 8. Найдите все положительные значения а, при которых система  единственное решение.
единственное решение.
Решение. Графиком уравнения  является окружность с центром в точке (7; 2), радиуса 3 и такая же окружность симметричная ей относительно оси Оу.
является окружность с центром в точке (7; 2), радиуса 3 и такая же окружность симметричная ей относительно оси Оу.
Графиком уравнения  является множество окружностей с центром в точке (-3; -1), радиуса а, где а > 0 по условию задачи.
является множество окружностей с центром в точке (-3; -1), радиуса а, где а > 0 по условию задачи.
Если система имеет единственное решение, то а = ЕР = АЕ - АР или а = ЕК = ЕВ + ВК.
В остальных случаях система либо не имеет решения, либо имеет три решения. Тогда
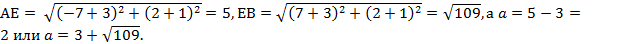 EM = 8 < EK, EN =
EM = 8 < EK, EN = 
Ответ:  или
или 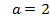
М
К
А 2 N В
-7 Р 7
Е
Метод решения задания с параметром с помощью нахождения области значений функции.
Задача 9. Найдите все значения р, при которых уравнение  не имеет корней.
не имеет корней.
Решение. Представим уравнение в виде  и преобразуем ее левую часть.
и преобразуем ее левую часть. 
 Рассмотрим функцию
Рассмотрим функцию
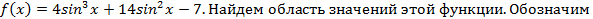
 .
. 
 .
. 
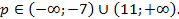
Ответ: 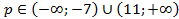 .
.
Задача 10. Укажите наименьшее значение b, при котором уравнение  имеет хотя бы один корень.
имеет хотя бы один корень.
Решение. Преобразуем данное уравнение в виде:

Рассмотрим функцию 
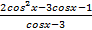 .
.
 .
.
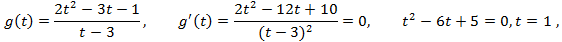
 .
. 
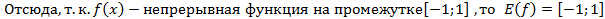
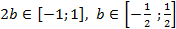 . Ответ:
. Ответ: 
Задача 11. Найдите все значения параметра а, при которых уравнение  имеет корни и все корни неотрицательны.
имеет корни и все корни неотрицательны.
Решение. 

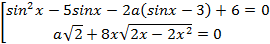
2)Из второго уравнения получим 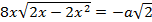 . Т.к.
. Т.к. 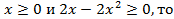
 Рассмотрим функцию
Рассмотрим функцию  .
.
 .
. 
3) 

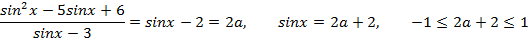
 . Т.к.
. Т.к.  , то
, то  .
.
Ответ: 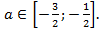
Метод использования свойств четности и нечетности функции.
Задача 12. Найти все значения параметра а, при которых уравнение  имеет единственное решение.
имеет единственное решение.
Решение. Имеем  . Обозначим x – 1=t. Получим
. Обозначим x – 1=t. Получим  . Функция
. Функция  .
.  Достаточность для всех a:
Достаточность для всех a: 
Задача 13.Найдите все значения параметра а, при которых неравенство  имеет единственное решение.
имеет единственное решение.
Решение. cosx  ;
;  Тогда
Тогда 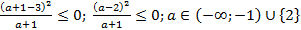 3) докажем достаточность единственности решения. Если
3) докажем достаточность единственности решения. Если 
При 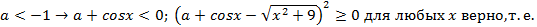
 Ответ: 2.
Ответ: 2.
Задача 14. Найдите все значения параметра а, при которых система 
Решение. 
Если поменять местами х и у то ничего не меняется. Поэтому, если 

Относительно z – наше выражение четное. Для единственности решения z=0.

ОДЗ:  Тогда из первого уравнения
Тогда из первого уравнения  . Следует 2 = а + 1,
. Следует 2 = а + 1,
а = 1. Проверим достаточность.  Ответ: а = 1
Ответ: а = 1
Задача 15. Найти все значения параметра а, при каждом из которых уравнение  имеет единственный корень.
имеет единственный корень.
Решение. Данное уравнение относительно х четное, поэтому для единственности решения необходимо, чтобы х=0. Тогда  . Обозначим
. Обозначим  . Тогда
. Тогда  Проверим достаточность. При
Проверим достаточность. При 
При  Ответ: а =3; а =7.
Ответ: а =3; а =7.
Геометрический метод.Использование формулы расстояния между точками.
Задача 16. Найдите все значения параметра а, при каждом из которых система уравнений  имеет единственное решение.
имеет единственное решение.
Решение. Первое уравнение – это уравнение окружности с центром (0 ; 4) и радиуса 4. Второе уравнение – это формула вида АВ + АС = ВС, где А(х ; у), В(0 ; 12), С(а ; 0). Тогда 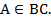
В Единственное решение, когда ВС касается
окружности. Тогда треугольник АВЕ 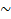 треугольнику ОВС.
треугольнику ОВС.
ОВ = 12, ОЕ = 4, ВЕ = 8, АЕ = 4 Тогда по теореме Пифагора АВ = 4 
А
С О С
 . Получается
. Получается  Ответ:
Ответ: 
Задача 17.Найдите все значения параметра а, при каждом из которых система уравнений  имеет ровно два решения.
имеет ровно два решения.
Решение. Первое уравнение – это уравнение окружности с центром Е(6 – а ; а) и радиуса 3  .
. 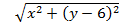 - расстояние между точками А (х; у) и В(0 ; 6);
- расстояние между точками А (х; у) и В(0 ; 6); 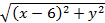 - расстояние между точками А (х; у) и С(6 ; 0); ВС =
- расстояние между точками А (х; у) и С(6 ; 0); ВС =  АВ + АС = ВС
АВ + АС = ВС
Докажем, что точка Е 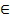 ВС.
ВС. 
В Следует точка Е принадлежит ВС. Если Е – середина ВС, то
два решения. Точка Е(3 ; 3). Следует а = 3. Ответ: а = 3.
6
6 
6 С
Задача 18.Найдите все значения параметра а, при каждом из которых система уравнений  имеет более одного решения.
имеет более одного решения.
Решение. Рассмотрим графики этих уравнений. График первого уравнения – это прямая.  - расстояние между точками O(0 ; 0) и A(х ; у);
- расстояние между точками O(0 ; 0) и A(х ; у);  -расстояние между точками B(a ; 2a) и A(х ; у);
-расстояние между точками B(a ; 2a) и A(х ; у);  Имеем ОА + АВ = ОВ. Тогда точки О, А и В лежат на одной прямой, т.е.
Имеем ОА + АВ = ОВ. Тогда точки О, А и В лежат на одной прямой, т.е.  - уравнение прямой. Если эти две прямые имеют более одной общей точки, то они совпадают. Т.к.
- уравнение прямой. Если эти две прямые имеют более одной общей точки, то они совпадают. Т.к.  проходит через начало координат, то
проходит через начало координат, то  Ответ:
Ответ: 
Задача 19. Найдите все значения параметра а, при каждом из которых система уравнений 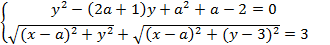 имеет единственное решение.
имеет единственное решение.
Решение. Рассмотрим графики уравнений:  . Тогда
. Тогда  прямые, параллельные оси Ох, причем
прямые, параллельные оси Ох, причем 
 – р/асстояние между точками А(х;у) и В(а;0);
– р/асстояние между точками А(х;у) и В(а;0);  - расстояние между точками А(х;у) и С(а;3); Т .к. расстояние от точки (а ; 0) до (а ; 3) равно 3, то точка А принадлежит отрезку ВС.
- расстояние между точками А(х;у) и С(а;3); Т .к. расстояние от точки (а ; 0) до (а ; 3) равно 3, то точка А принадлежит отрезку ВС.

3

А
Единственное решение получится, если 
Ответ: 
Периодические функции.
Задача 20. Найдите все пары (х;у),  , удовлетворяющие системе
, удовлетворяющие системе  , где f – периодическая функция с периодом Т=2, определенная на всей числовой прямой, причем f(x)
, где f – периодическая функция с периодом Т=2, определенная на всей числовой прямой, причем f(x)  1.
1.
Решение. Введем обозначения  Тогда
Тогда  ; Т.к.
; Т.к.  то
то 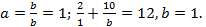 Получим
Получим  Построим график функции
Построим график функции  – периодическая.
– периодическая.
4 
 Т.к.
Т.к.  то
то  то
то  или
или  Ответ:
Ответ:  или
или 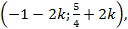
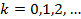
4 
3
-1 1 3 5 7
Задача 21.Найдите все значения параметра а, большие 1, при каждом из которых уравнение  f – периодическая функция с периодом Т=4, определенная на всей числовой прямой, причем f(x)
f – периодическая функция с периодом Т=4, определенная на всей числовой прямой, причем f(x)  .
.
Решение. Построим график функции f(x) 
 и т.к.
и т.к. 
4,5 
-8 -6 -4 -2 1 2 4 6 8 9
Построим график функции  так, чтобы было 6 точек пересечения. Т.к.
так, чтобы было 6 точек пересечения. Т.к.  - возрастающая функция. Шестая точка пересечения при
- возрастающая функция. Шестая точка пересечения при  =
=  – непрерывная и возрастающая функция при а>1. Поэтому, при
– непрерывная и возрастающая функция при а>1. Поэтому, при  при
при  Тогда уравнение
Тогда уравнение  единственное решение при
единственное решение при  Ответ:
Ответ: 
Задача 22.Найдите все значения параметра а, при каждом из которых уравнение  f –четная периодическая функция с периодом Т=2, определенная на всей числовой прямой, причем f(x)
f –четная периодическая функция с периодом Т=2, определенная на всей числовой прямой, причем f(x)  .
.
Решение. При  периодическая функция
периодическая функция  Бесконечно много решений
Бесконечно много решений  При
При 
 .
.
а
-5 5
При 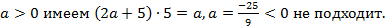 При
При  . Ответ:
. Ответ:  .
.
Еще раз графический метод.
Задача 23.Найдите все значения параметра а, при каждом из которых уравнение 
Решение. ОДЗ: 
 . Представим уравнение в виде:
. Представим уравнение в виде:  . Рассмотрим график функции
. Рассмотрим график функции  . Тогда
. Тогда  . Т.к.
. Т.к.  то это уравнение полуокружности с центром (-2;0) и радиуса 3. А
то это уравнение полуокружности с центром (-2;0) и радиуса 3. А 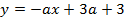 - это пучок прямых, проходящих через точку (3;3).
- это пучок прямых, проходящих через точку (3;3).
Единственное решение, когда прямая касается полуокружности и проходит между х=-5 и х=1, включая х=1. Касается – это проходит через точку (-2;3).  . Проходит через точку (1;0),
. Проходит через точку (1;0),  Не проходит через точку (-5;0),
Не проходит через точку (-5;0),  . Ответ:
. Ответ:  .
.
Еще раз четность функции.
Задача 24.Найдите все значения параметра а, при каждом из которых уравнение 
Решение.  – четная функция. Поэтому для единственности решения необходимо
– четная функция. Поэтому для единственности решения необходимо  Проверим достаточность:
Проверим достаточность: 
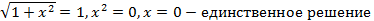 . Ответ:
. Ответ: 
Аналитический метод
Задача 25.При каких значениях параметров а и b система 
имеет бесконечно много решений?
Решение.
На координатной плоскости хОу множество точек  , удовлетворяющих любому из
, удовлетворяющих любому из
уравнений системы — прямые. А тогда решением системы будут точки пересечения этих
прямых. Поэтому исходная система будет иметь бесконечное множество решений в том и
только в том случае, когда эти прямые совпадают. В общем случае две прямые, заданные
уравнениями  и
и  совпадают, если
совпадают, если  и
и  (при
(при  они имеют одну точку пересечения, при
они имеют одну точку пересечения, при  и
и 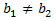 точек пересечения у них нет). Следовательно, система будет иметь бесконечно много решений в том случае, когда совместна система
точек пересечения у них нет). Следовательно, система будет иметь бесконечно много решений в том случае, когда совместна система  ,
,  где
где  и
и  .
.
Решая систему, получаем 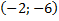 ,
,  .
.
Ответ:  ,
,  .
.
Дата добавления: 2018-04-04; просмотров: 2252; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
