За методом найменших квадратів
Для аналізу та синтезу САР статичні характеристики об’єкта регулювання зручно мати у вигляді простих аналітичних виразів
.
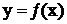Більшість функцій, які застосовують на практиці, можна розкласти в ряд Тейлора (степеневий ряд). При обмеженій кількості членів ряд Тейлора для функції однієї змінної матиме вигляд полінома
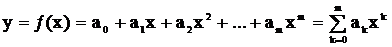, (4)
де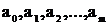 
– постійні коефіцієнти; 
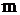– степінь полінома. Апроксимацію емпіричних залежностей поліномом застосовують найчастіше ще й тому, що математичні властивості поліномів добре вивчені і з ними легко працювати.
Коефіцієнти полінома найдоцільніше визначати методом найменших квадратів (МНК), при якому немає жорсткої залежності степеня полінома від кількості N отриманих експериментальних пар даних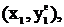 
..., 
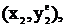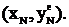
За методом МНК шукають такі значення коефіцієнтів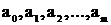 
, які забезпечують найменшу суму І квадратів різниці між розрахованими за рівнянням полінома та експериментальними значеннями вихідної величини
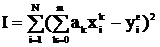, (5)
де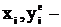 
експериментальні значення вхідної та вихідної величини.
Умову, при якій функція І має екстремум, записують у вигляді
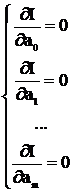або згорнуто 
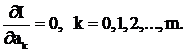(6)
Підставляючи І з формули (5) в умову (6), одержують систему з m+1 рівняння, з якої визначають коефіцієнти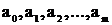 
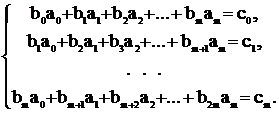, (7)
де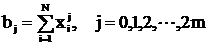 
, 
.
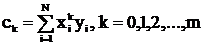Систему рівнянь (7) можна розв’язувати методами Гауса, Крамера, оберненої матриці чи будь-яким іншим числовим методом.
|
|
|
Всі наведені співвідношення методу найменших квадратів можна записати компактніше, якщо застосувати векторно-матричну форму запису. Введемо матриці
, 
, 
, 
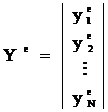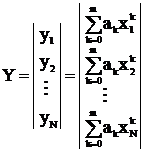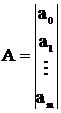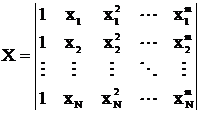, (8)
де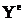 
– матриця експериментальних значень вихідної величини; 
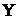– матриця значень вихідної величини, розрахованих за моделлю; 
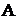– матриця шуканих коефіцієнтів моделі; 
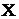– матриця, складена з експериментальних значень вхідної величини.
Тоді в векторній формі рівняння полінома (4) можна записати у вигляді
,
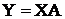а функцію (5) як
,
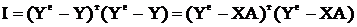де ‘т’ – символ транспонування матриці.
Далі маємо
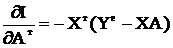. (9)
Позначимо вектор оптимальних параметрів полінома, при яких І набуває найменшого значення, через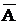 
, тоді
,
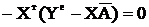звідки
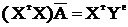
і відповідно матрицю коефіцієнтів, що забезпечує мінімум суми квадратів відхилень розрахункових значень апроксимуючого поліному від експериментальних значень, шукають з рівняння
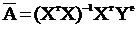, (10)
де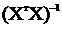 
– матриця, обернена до матриці 
. 
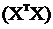Методика побудови статичної моделі у вигляді полінома така. Звичайно починають із найпростішої моделі – полінома першого порядку (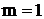 
) та розраховують коефіцієнти 
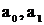, які забезпечують мінімальне значення суми І квадратів різниці між розрахованими за поліномом та експериментальними значеннями вихідної величини. За знайденим поліномом розраховують зведену похибку для кожного значення вхідної величини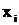 
|
|
|
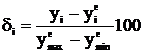, % (11)
де 
, 
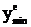– відповідно максимальне і мінімальне експериментальні значення вихідної величини; 
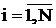. Якщо максимальне значення зведеної похибки 
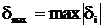не перевищує допустиме значення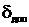 
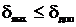, (12)
то отримана статична модель є адекватною досліджуваному об’єкту регулювання. Якщо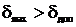 
, то степінь полінома 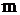збільшують на 1, знаходять його коефіцієнти, знову порівнюють похибку апроксимації з допустимим значенням і т.д. Порядок полінома збільшують доти, доки не буде досягнуто виконання умови (12). Для вибраного полінома розраховують також середньоквадратичне відхилення розрахованих значень вихідної величини від експериментальних
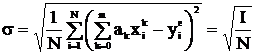. (13)
Слід зазначити, що із зростанням степеня полінома точність апроксимації зростає, але ускладнюється інтерпретація моделі. Крім того, чим більше коефіцієнтів містить модель, тим більше експериментів треба проводити. Мінімальна кількість експериментів дорівнює кількості параметрів моделі, але для перевірки адекватності моделі в статистичному розумінні кількість дослідів повинна бути більшою.
Дата добавления: 2018-04-04; просмотров: 211; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!