Условные данные по субъектам России за 199Хг
| Субъект РФ | Y | X |
| Субъект-1 | 68,8 | 45,1 |
| Субъект-2 | 61,2 | 59,0 |
| Субъект-3 | 59,9 | 57,2 |
| Субъект-4 | 56,7 | 61,8 |
| Субъект-5 | 55,0 | 58,8 |
| Субъект-6 | 54,3 | 47,2 |
| Субъект-7 | 49,3 | 55,2 |
Расчеты удобно проводить с использованием таблицы типа табл. 2.2.
Таблица 2.2
Промежуточные расчетные данные
| № п/п | уi | xi | уi xi | 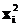
| 
| 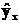
| yi - 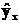
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 68,8 | 45,1 | 3102,88 | 2034,01 | 4733,44 | 61,3 | 7,5 |
| 2 | 61,2 | 59,0 | 3610,80 | 3481,00 | 3745,44 | 56,5 | 4,7 |
| 3 | 59,9 | 57,2 | 3426,28 | 3271,84 | 3588,01 | 57,1 | 2,8 |
| 4 | 56,7 | 61,8 | 3504,06 | 3819,24 | 3214,89 | 55,5 | 1,2 |
| 5 | 55,0 | 58,8 | 3234,00 | 3457,44 | 3025,00 | 56,5 | -1,5 |
| 6 | 54,3 | 47,2 | 2562,96 | 2227,84 | 2948,49 | 60,5 | -6,2 |
| 7 | 49,3 | 55,2 | 2721,36 | 3047,04 | 2430,49 | 57,8 | -8,5 |
| Итого | 405,2 | 384,3 | 22162,34 | 21338,41 | 23685,76 | 405,2 | 0,0 |
| Средн. | 57,89 | 54,90 | 3166,05 | 3048,34 | 3383,68 | - | - |
| s | 5,74 | 5,86 |
Решение. В табл. 2.2 графы 2 и 3 - наблюденные пары значений переменных Y и Х, графы 4-6 вычисляются непосредственно на основе граф 2 и 3. Остальные графы в этом примере не используются.
По формулам (2.7) рассчитаем параметры регрессии b0 и b1, получим искомое уравнение регрессии:
|
|
|
 = 76,88 - 0,35x. = 76,88 - 0,35x.
| (2.10) |
Смысл параметра уравнения b1: при увеличении среднесуточного дохода на 1 руб. расход на продовольствие сократится на 0,35% от общей суммы среднесуточного расхода. Свободный член b0 смысла не имеет.
Связь коэффициентов регрессии и корреляции
Если значение bo из формул (2.7) подставить в уравнение регрессии (2.2), то после преобразований получим уравнение регрессии в отклонениях (прямая проходит через начало координат - точку ( 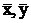 )).
)).
Преобразуем это уравнение: разделим обе части на sy, умножим и разделим правую часть на sx, получим:
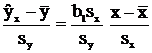 .
.
| где коэффициент r = b1 sx/sy показывает, на сколько величин sy изменится в среднем Y, если Х увеличится на одно значение sx. | (2.11) |
Другой вариант формулы для расчета r:
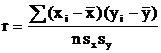 . .
| (2.12) |
Статистика r - выборочный коэффициент корреляции - отражает тесноту статистической связи случайных величин Х и Y. Свойства коэффициента корреляции (рис. 2.1):
1. -1 £ r £ 1. Чем ближе модуль ç r ç к 1, тем теснее связь Х и Y.
2. Если r = ± 1, то связь между Х и Y - функциональная и линейная.
|
|
|
3. Если r = 0, то линейная корреляционная связь между СВ Х и Y отсутствует.
4. Коэффициент r является непосредственной оценкой генерального коэффициента корреляции r между Х и Y лишь в случае двухмерного НЗР случайной величины (Х, У). В других случаях r не является строгой мерой взаимосвязи переменных.
у у у






 r = +1 r » +0,8 r » +0,5
r = +1 r » +0,8 r » +0,5
Дата добавления: 2018-04-04; просмотров: 131; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
