Решение одномерной осесимметричной задачи магнитостатики аналитически и методом конечных элементов
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего образования
Пермский национальный исследовательский
Политехнический университет
Кафедра конструирования и технологий в электротехнике
ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ
Методические указания
к практическим работам
Пермь 2018
УДК 519.63
Рецензент
доцент кафедры КТЭ, канд. техн. наук Е.В. Субботин
(Пермский национальный исследовательский
политехнический университет)
Вычислительные методы исследования электромагнитных полей. Методические указания к практическим работам / Сост. А.Г. Щербинин. ПНИПУ. Пермь, 2018. 15 с.
Приводятся методические указания к практическим работам и варианты заданий по дисциплинам «Вычислительные методы в электротехнике» и «Вычислительные методы в электротехнологии» для студентов академической магистратуры по направлению 13.04.02 «Электроэнергетика и электротехника».
УДК 519.63
Ó ПНИПУ, 2018
Решение одномерной осесимметричной задачи электростатики аналитически и методом конечных элементов
Рассмотрим электростатическую задачу определения потенциала коаксиального кабеля (рис. 1.1). Уравнения Лапласа в цилиндрической системе координат запишется следующим образом
 , (1.1)
, (1.1)
где  ,
,  ,
, 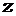 – координаты в цилиндрической системе координат;
– координаты в цилиндрической системе координат;  – электрический потенциал;
– электрический потенциал;  – абсолютная диэлектрическая проницаемость;
– абсолютная диэлектрическая проницаемость;  – электрическая постоянная, Ф/м;
– электрическая постоянная, Ф/м;  – относительная диэлектрическая проницаемость.
– относительная диэлектрическая проницаемость.

Рис. 1.1. Поперечное сечение коаксиального кабеля
Для плоскопараллельного поля в осесимметричной постановке  и
и 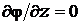 . Тогда уравнение (1.1) преобразуется к виду
. Тогда уравнение (1.1) преобразуется к виду
 , (1.2)
, (1.2)
Дифференциальное уравнение (1.2) дополним граничными условиями:
 . (1.3)
. (1.3)
Необходимо найти распределение потенциала по радиусу.
Применение метода Галёркина к уравнению (1.2) даст
 . (1.4)
. (1.4)
где  – приближенное решение;
– приближенное решение;  – весовая функция. В методе Галёркина весовые функции равны базисным функциям (функциям формы).
– весовая функция. В методе Галёркина весовые функции равны базисным функциям (функциям формы).
В результате применения метода Галеркина и последующих преобразований, получим
 . (1.5)
. (1.5)
Неизвестная функция  в уравнении (1.5) определяются соотношением
в уравнении (1.5) определяются соотношением
 . (1.6)
. (1.6)
Тогда
 (1.7)
(1.7)
Подставляя формулу (1.7) в первый интеграл уравнения (1.5), получим
 . (1.8)
. (1.8)
Поскольку на левой и правой границах задано граничное условие первого рода (1.3), то уравнение (1.5) с учетом (1.8) запишется следующим образом
 (1.9)
(1.9)
В уравнении (1.9) неизвестными являются 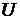 .
.
Функции формы  одномерного симплекс элемента
одномерного симплекс элемента
 . (1.10)
. (1.10)
где  – длина конечного элемента.
– длина конечного элемента.
Для одномерного симплекс-элемента матрица градиентов запишется
 . (1.11)
. (1.11)
С учетом выражения (1.11) запишем
 (1.12)
(1.12)
Уравнение (1.12) перепишем в виде
 , (1.13)
, (1.13)
Здесь:  .
.
Размерности локальных матриц
 ;
;  .
.
Определим члены уравнения для текущего элемента
 (1.14)
(1.14)
Или по другому, при условии что  и
и  , запишем
, запишем
 (1.15)
(1.15)
Распределение напряженности электрического поля по известному распределению потенциал определяется по формуле
 . (1.16)
. (1.16)
Аналитические выражения для определения потенциала и напряженности электрического поля по радиусу двухслойной изоляции коаксиального кабеля запишутся как:

 (1.17)
(1.17)

 (1.18)
(1.18)
 (1.19)
(1.19)
ЗАДАНИЕ
Дан коаксиальный кабель с двухслойной изоляцией. К внутреннему проводнику приложен потенциал  , а внешний проводник имеет нулевой потенциал. Найти распределение потенциала и напряженности электрического поля по толщине изоляции. Варианты заданий представлены в таблице 1.1.
, а внешний проводник имеет нулевой потенциал. Найти распределение потенциала и напряженности электрического поля по толщине изоляции. Варианты заданий представлены в таблице 1.1.
Таблица 1.1. Варианты заданий
| Вариант № |  , мм , мм
|  , мм , мм
|  , мм , мм
|  , мм , мм
|  , мм , мм
| 
| 
| 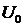 , кВ , кВ
|
| 1 | 10 | 15 | 25 | 0,5 | 1 | 2 | 3 | 110 |
| 2 | 10 | 16 | 25 | 0,6 | 0,9 | 3 | 2 | 110 |
| 3 | 10 | 17 | 25 | 0,7 | 0,8 | 2 | 4 | 110 |
| 4 | 10 | 18 | 25 | 0,8 | 0,7 | 4 | 2 | 110 |
| 5 | 10 | 19 | 25 | 0,9 | 0,6 | 3 | 4 | 110 |
| 6 | 10 | 20 | 25 | 1 | 0,5 | 4 | 3 | 110 |
| 7 | 10 | 17,5 | 32,5 | 0,5 | 1 | 3 | 5 | 220 |
| 8 | 10 | 19 | 32,5 | 0,6 | 0,9 | 5 | 3 | 220 |
| 9 | 10 | 20,5 | 32,5 | 0,7 | 0,8 | 4 | 5 | 220 |
| 10 | 10 | 22 | 32,5 | 0,8 | 0,7 | 5 | 4 | 220 |
| 11 | 10 | 23,5 | 32,5 | 0,9 | 0,6 | 4 | 6 | 220 |
| 12 | 10 | 25 | 32,5 | 1 | 0,5 | 6 | 4 | 220 |
Отчет
1. Титульный лист
2. Задание
3. Постановка задачи
4. Глобальная система алгебраических уравнений с расшифровкой локальной матрицы коэффициентов
5. Аналитические формулы
6. Матрица коэффициентов
7. Результаты вычислений
| № узла |  , мм , мм
| 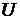 , В , В
|  , В , В
|  , % , %
|
| № элемента |  , мм , мм
|  , В/мм , В/мм
|  , В/мм , В/мм
|  , % , %
|
8. Графики  ,
, 
9. Емкость
10. Выводы
Решение одномерной осесимметричной задачи магнитостатики аналитически и методом конечных элементов
Рассмотрим магнитостатическую задачу определения потенциала одиночного проводника (рис. 2.1). Уравнение для магнитного потенциала в одномерной осесимметричной постановке запишется
 , (2.1)
, (2.1)
где  – магнитный потенциал (в одномерной осесимметричной постановке направлен по координате
– магнитный потенциал (в одномерной осесимметричной постановке направлен по координате 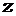 );
);  – абсолютная магнитная проницаемость;
– абсолютная магнитная проницаемость;  – относительная магнитная проницаемость;
– относительная магнитная проницаемость;  – магнитная постоянная;
– магнитная постоянная;  – плотность тока;
– плотность тока;  – заданный ток,
– заданный ток,  – сечение токопроводящей жилы.
– сечение токопроводящей жилы.
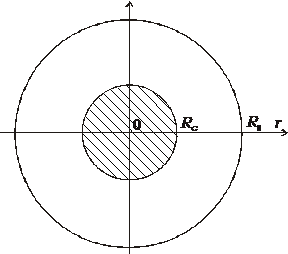
Рис. 2.1. Поперечное сечение одиночного проводника
Необходимо найти распределение магнитного потенциала  по радиусу.
по радиусу.
Применение метода Галёркина к уравнению (1.1) даст
 , (2.2)
, (2.2)
где  – приближенное решение.
– приближенное решение.
В результате применения метода Галеркина и последующих преобразований, получим
 . (2.3)
. (2.3)
Неизвестная функция  в уравнении (17) определяются соотношением
в уравнении (17) определяются соотношением
 . (2.4)
. (2.4)
Тогда
 (2.5)
(2.5)
Подставляя формулу (2.5) в первый интеграл уравнения (2.3), запишем
 . (2.6)
. (2.6)
Поскольку в уравнении (2.3) выражение  содержит множитель
содержит множитель  , то в этом случае его можно использовать в качестве граничного условия на бесконечно удаленной границе, которое можно записать в виде граничного условие Робина
, то в этом случае его можно использовать в качестве граничного условия на бесконечно удаленной границе, которое можно записать в виде граничного условие Робина  . Или
. Или
 . (2.7)
. (2.7)
Здесь:  – радиус границы, на которой задано условие бесконечной границы;
– радиус границы, на которой задано условие бесконечной границы;  – расстояние от проводника до границы области, на которой задано условие бесконечной границы.
– расстояние от проводника до границы области, на которой задано условие бесконечной границы.
Тогда
 (2.8)
(2.8)
Уравнение (2.3) с учетом выражений (2.6) и (2.8) запишется
 (2.9)
(2.9)
Функции формы и матрица градиентов одномерного симплекс-элемента определяются выражениями (1.10) и (1.11). Тогда уравнение (2.9) запишется в виде
 (2.10)
(2.10)
Уравнение (2.10) перепишем в виде
 . (2.11)
. (2.11)
Здесь:  ;
;  ;
;  .
.
Размерности локальных матриц
 ;
;  .
.
Определим члены уравнения для текущего элемента
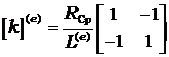 (2.12)
(2.12)
На правой границе расчетной области матрица 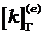 определится как
определится как
 . (2.13)
. (2.13)
Вектор столбец свободных членов определится выражением
 . (2.14)
. (2.14)
ЗАДАНИЕ
Дан одиночный проводник (рис. 2.1), по которому протекает ток. Найти распределение магнитного потенциала и напряженности магнитного поля. Варианты заданий представлены в таблице 2.1.
Таблица 2.1. Варианты заданий
| Вариант № | 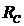 , мм , мм
|  , мм , мм
|  , мм , мм
|  , мм , мм
|  , A , A
|
| 1 | 10 | 55 | 0,5 | 1 | 1500 |
| 2 | 11 | 54 | 0,6 | 1 | 2000 |
| 3 | 12 | 53 | 0,7 | 1 | 2500 |
| 4 | 13 | 52 | 0,8 | 1 | 3000 |
| 5 | 14 | 51 | 0,9 | 1 | 3500 |
| 6 | 15 | 50 | 1 | 1 | 4000 |
| 7 | 10 | 49 | 0,5 | 1 | 1500 |
| 8 | 11 | 48 | 0,6 | 1 | 2000 |
| 9 | 12 | 47 | 0,7 | 1 | 2500 |
| 10 | 13 | 46 | 0,8 | 1 | 3000 |
| 11 | 14 | 45 | 0,9 | 1 | 3500 |
| 12 | 15 | 44 | 1 | 1 | 4000 |
Отчет
1. Титульный лист
2. Задание
3. Постановка задачи
4. Локальные матрицы коэффициентов и свободных членов
5. Аналитические формулы по определению напряженности магнитного поля 
6. Результаты вычислений
| № узла |  , мм , мм
|  , В×с/м , В×с/м
|
Напряженность магнитного поля определяется по формуле 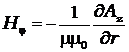 .
.
| № элемента |  , мм , мм
|  , A/мм , A/мм
|  , A/мм , A/мм
| 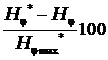 , % , %
|
7. Графики  ,
, 
8. Выводы
Дата добавления: 2018-04-04; просмотров: 550; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
