Понятие социологического индекса. Логические индексы (логический квадрат, логический прямоугольник)

⇐ ПредыдущаяСтр 19 из 24Следующая ⇒

В социологии рассматриваемая традиция нередко проявляется в виде стремления социолога к построению так называемых индексов для измерения латентной установочной переменной.

Индекс – численные показатели, образованные путем комбинации индикаторов(вопрос в анкете).Индекс - обобщенный показатель, сформированный из исходных посредством математических операций. Исходными показателями для индекса могут быть сами эмпирические индикаторы либо какие-то, производные от эмпирических индикаторов, показатели. Например, показатель оценки качества «курса лекций», полученный посредством логического прямоугольника, или показатель удовлетворенности учебой, сформированный посредством логического квадрата.

Создание индекса – процедура, которая осуществляется как на этапе построения программы, так и на этапе анализа, но в анкете она не присутствует.

Методы построения:

Перешел бы?	Пришли бы вы?
	да	нет	з/о
да	f	е	d
Нет	а	f	в
з/о	в	d	i

1)Метод логического квадрата - применим к шкале любого уровня, достаточно распространен.

. Задаем респонденту, студенту социологического факультета одного из названных вузов, два взаимодополняющих друг друга вопроса:

1. Представьте себе, что у вас есть возможность перейти на другой социологический факультет. Перешли бы вы?1) да, перешел бы нет,2) не перешел бы 3)затрудняюсь ответить (з/о)

Представьте себе, что вы нигде не учитесь. Пришли бы вы или нет учиться на ваш факультет? (аналогичные ответы)

Проанализируем все возможные сочетания вариантов ответа на эти два вопроса. Таких сочетаний 9, т. е. после сбора информации мы можем столкнуться с девятью ситуациями. Каждая из них требует интерпретации до проведения пилотажа. Возможная ситуация отмечена буквами а, b, с, d, e, f.Мах удовлетворенность будет наблюдаться в ситуации a, миним. — в ситуации e, средняя — в ситуации c. . Буквой fобозначены две ситуации, которые практически не м. встретиться в данных, ибо содержат в себе противоречие. Две ситуации, обозначенные b, в определенной мере идентичны. Степень удовлетворенности для этих случаев меньше, чем максимальная, и больше, чем средняя. две одинаковые ситуации, обозначенные буквой d. Им соответствует степень удовлетворенности меньшая, чем средняя, и большая, чем минимальная. Логический квадрат называется логическим в силу того, что исследователь проводит только логические операции, а квадратом — потому что такова его форма существования. На входе мы имеем трехчленную шкалу, а на выходе шкалу порядков с пятью градациями. Можем закодировать или присвоить шкальные значения ситуациям так, чтобы выполнялось условие: a>b>c>d>e.

Например, а=5, b=4, с=3, d=2, e=l.

С помощью логического квадрата мы определяем удовлетворенность учебой только отдельно взятого студента.

2)Метод логического прямоугольника.Данный метод является упрощенным или упрощенным методом логического квадрата. Представим себе, что мы изучаем рейтинг преподавателей, при этом будем операться на мнение студентов. Задаем три вопроса

1) Как вы считаете содержателен курс лекций? Да нет з/о

2) Как вы считаете интересно ли читает лектор данный курс лекций? Да нет з/о

3) Понимаете ли Вы материал данного курса?Да нет з/о

Содер	Инт.	Поним.
+	+	+	1мето-отл
-	+	+	2место-хор
+	-	+	2место-хор
+	+	-	3место-удовл
-	+	+	3место-удовл
+	-	-	4место-плохо
-	-	-	5место-оч.плохо

Построение индексов, характеризующих группу респондентов

Индексы для равнения групп.

Теперь представим себе, отвлекаясь от рассмотренных нами задач, что нам нужен индекс, характеризующий группу респондентов. При этом у нас есть оценки для каждого респондента, полученные по шкале порядков. Логика формирования индекса на основе шкалы порядка одинакова независимо от того, каким способом получена исходная порядковая шкала и сколько на ней градаций (пунктов шкалы). Возьмем, к примеру, случай, когда по каждому респонденту есть оценка «уровня беспокойства» трудоустройством по специальности после окончания вуза, полученная по порядковой шкале с пятью градациями. Выше был приведен этот эмпирический индикатор как вопрос вида «Насколько Вы уверены, что найдете работу по специальности после окончания вуза?». Перед нами стоит задача получения оценки уровня беспокойства/ уверенности в целом по группе респондентов. Для начала несколько упростим ситуацию и представим себе, что исходно имеем дело со шкалой с тремя градациями:

— уверен, что найду

— и да, и нет

— совсем не уверен, что найду

Естественным образом, оценкой «уровня беспокойства» для группы может служить разница между числом «уверенных» и числом «неуверенных» в группе. Но не абсолютная разница, а относительная, т. е. доля этой разницы в общем числе респондентов данной группы. Тогда значение индекса не зависит от объема группы и по нему можно сравнивать «уровни беспокойства» групп разного объема.

Если обозначим через n₊ — число «уверенных», n — число «неуверенных», а через n₀ — число «нейтральных», то индекс I будет иметь следующий вид:

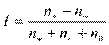
Какой бы индекс социолог ни использовал, он необходимым образом выясняет свойства этого индекса, т. е. выясняет правила его «поведения». Данный индекс обладает следующими свойствами. Он принимает максимальное значение, равное 1, тогда, когда все респонденты в группе уверены, что найдут работу по специальности. Он принимает минимальное значение, равное —1, тогда, когда все респонденты не уверены, что найдут работу по специальности. Индекс равен нулю, если число «уверенных» равно числу «неуверенных». Положительное значение индекса говорит о том, что уверенных больше, чем неуверенных. И соответственно, отрицательное значение появится в ситуации, когда число неуверенных больше, чем уверенных. Понятно, что в группах с одинаковой разницей (отличной от нуля) между числом уверенных и неуверенных (это называется абсолютной разницей в отличие от относительной), значение индекса будет больше в той группе, где меньше нейтральных ответов.

А теперь, опираясь на те же рассуждения, можно предложить аналогичный индекс и для случая пяти градаций. Обозначим через n_a — число уверенных студентов, n_b — число скорее уверенных, чем нет, n_c — число нейтральных, п_d —число не очень уверенных и n_e — число скорее неуверенных. Тогда можно предложить индекс следующего вида:

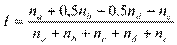
Если в предыдущей формуле все коэффициенты при разных n (частотах) были равны единице, то в этой формуле появились коэффициенты разные (1 и 0,5). Это означает, что отдельно взятая градация вносит разный вклад, разную долю в значение индекса. Коэффициент, равный 0,5 перед n_b и n_d вводится для того, чтобы сделать равноправными «не очень уверенных» и «скорее неуверенных». Это во-первых. Во-вторых, вклад тех, кто «не очень», в два раза меньше, чем вклад тех, кто «очень». И наконец, рассмотрим ситуацию, когда в группе нет респондентов уверенных, нейтральных, не очень уверенных, совсем неуверенных, а все респонденты скорее уверены, чем нет. Тогда значение индекса будет равно 0,5. Аналогичные рассуждения можно продолжить для выяснения всех остальных свойств индекса.

Индекс, который мы рассматриваем, имеет достаточно простую, прозрачную конструкцию. Возникает вопрос, что будет, если число градаций на порядковой шкале увеличить. Самый простой ответ на этот вопрос обусловлен существованием интересного феномена в методической социологии. Назовем его условно для образности и яркости «законом триад». Какое бы исследование ни проводилось, социолог пользуется этим законом. Например, выбирает предприятия, территориальные образования, исходя из простой схемы: большое — среднее — малое. Выбирает для опроса студенческие группы: хорошие — средние — плохие. Анализирует отдельно различные группы по доходу: богатые — средние — бедные. Могут быть триады типа:

— удовлетворенные — и да, и нет — не удовлетворенные

— уверенные — и да, и нет — неуверенные

— вероятные — мало вероятные — невероятные

— интересующиеся — и да, и нет — не интересующиеся

Список можно продолжать до бесконечности, но не в этом дело. Для нас с вами важно, что в группе, например, «богатых» можно в свою очередь ввести новую триаду:

— богатые, но не очень — достаточно богатые — очень богатые,

А, например, между группами «удовлетворенных» и тех, кто «и да, и нет», также можно ввести новую триаду. Это очень удобный и простой способ, и для создания порядковых шкал, и для трансформации шкал, т. е. увеличения или уменьшения числа градаций на шкале. Разумеется, речь идет о так называемых сбалансированных шкалах. К ним относятся порядковые шкалы, на которых есть нейтральное положение и число «положительных» позиций равно числу «отрицательных». Сбалансированные шкалы пришли в социологию из психологии, где при измерениях опираются на модель «стимул — реакция». Соответственно, предполагается, что реакция может быть положительной, нейтральной и отрицательной.

Вернемся к задаче формирования индекса для характеристики группы в случае, когда исходные порядковые шкалы имеют большее число градаций, чем пять. В этом случае можно преобразовать исходную шкалу в шкалу с меньшим числом градаций и предложенным способом вычислить групповой индекс. Но следует иметь в виду, что преобразовать необходимо в сбалансированную шкалу. Если же этого нельзя сделать, то возможно проводить сравнения различных групп респондентов на основе других показателей, например на так называемых мерах центральной тенденции. О них будем говорить в соответствующем разделе книги.

Формирование аналитических индексов может быть отнесено и к отдельно взятому респонденту. Совершенно ясно, что с помощью прямо поставленных вопросов или с помощью логических индексов можно измерить очень ограниченное число свойств социальных объектов. Перейдем к рассмотрению еще одного приема измерения, который может быть обозначен как формирование шкалы суммарных оценок.

Впервые такого рода шкалу использовал в 1929—1931 гг. Р. Лайкерт (Ликерт) (R. Licert) для измерения расовых, национальных установок. Обычно социолог, «изобретая» некоторую шкалу суммарных оценок, называет ее шкалой типа шкалы Лайкерта, имея в виду процедуру измерения. Таким образом, шкалой называется и какая-то «линеечка», и алгоритм ее получения, т. е. сама процедура измерения. Процедуру измерения лучше называть шкалированием.

(Далее шкалу Ликерта будем называть шкалой Лайкерта ибо так её называют в большинстве случаев в русскоязычной литературе).

Дата добавления: 2018-02-28; просмотров: 3230; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 14 15 16 17 181920 21 22 23 Следующая ⇒

Мы поможем в написании ваших работ!