Обыкновенные дифференциальные уравнения

Вопросы по теме

1. Понятие дифференциальных уравнений.

2. Дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющимися переменными.

3. Дифференциальные уравнения второго порядка.

4. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Краткие теоретические сведения

Дифференциальным уравнениемназывается уравнение, связывающее между собой независимую переменную , искомую функцию и ее производные или дифференциалы.

Например,

Символически дифференциальное уравнение записывается так: 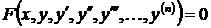, где - независимая переменная, - неизвестная функция, - производные этой функции.

Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.

Таковы, например, дифференциальные уравнения

Если неизвестная функция, входящая в дифференциальное уравнение, является функцией двух или большего числа независимых переменных, то дифференциальное уравнение называется уравнением в частных производных.

Например, дифференциальное уравнение .

Порядком дифференциального уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение.

Так, например, уравнения ; , являются уравнениями второго порядка; а уравнения , - первого порядка.

Решением (или интегралом) дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.

Общимрешением(илиобщим интегралом) дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения. Так, общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную.

Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находятся при определенных начальных значениях аргумента и функции.

Дифференциальным уравнением первого порядка называется уравнение, в которое входят производные (или дифференциалы) не выше первого порядка.

Примеры:

, - дифференциальные уравнения первого порядка с разделенными переменными;

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида .

Примеры: , .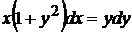

Для решения этого уравнения нужно сначала разделить переменные: , а затем проинтегрировать обе части полученного равенства: .

Примеры решения дифференциальных уравнений с разделяющимися переменными:

1. Найти общее решение уравнения .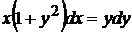

¨ Разделив переменные, имеем . Интегрируем обе части полученного уравнения: . Так как произвольная постоянная может принимать любые числовые значения, то для удобства дальнейших преобразований вместо мы написали . Потенцируя последнее равенство, получим . Это и есть общее решение данного уравнения. n

2. Найти частное решение уравнения , удовлетворяющее начальным условиям при .

¨ Разделив переменные, имеем . Проинтегрируем обе части полученного уравнения: , или . Это общее решение данного уравнения. Для нахождения значения произвольной постоянной подставим значения и в выражение для общего решения: , или , откуда . Следовательно, искомое частное решение, удовлетворяющее указанным начальным условиям, имеет вид .. n

Уравнение, содержащее производные (или дифференциалы) не выше второго порядка, называется дифференциальным уравнением второго порядка.

В общем виде уравнение второго порядка записывается следующим образом: .

Общее решение дифференциального уравнения второго порядка содержит две произвольные постоянные.

Примеры решения неполных дифференциальных уравнений второго порядка.

1. Найти общее решение уравнения .

¨Это не полное дифференциальное уравнение второго порядка вида . Полагаем ; тогда данное уравнение можно записать в виде , т.е. , откуда . Интегрируя последнее равенство, получим , т.е. .

Следовательно, , т.е. . Снова интегрируя, находим или . Это и есть общее решение данного уравнения.n

2. Найти частное решение уравнения 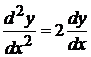, если и при .

¨Это неполное дифференциальное уравнение второго порядка вида . Положим ; тогда , и значит . Разделив в этом уравнении переменные и интегрируя, получим , . Следовательно, , т.е. 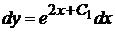. Интегрируя, находим общее решение данного уравнения . Для нахождения искомого частного решения подставим в соотношения и начальные данные:

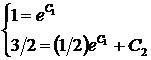или Откуда . Таким образом, искомое частное решение имеет вид .n

3. Найти частное решение уравнения , если и при .

¨ Это неполное дифференциальное уравнение второго порядка вида . Положим ; тогда . Подставив выражения для и в данное уравнение, получим . Разделив переменные и интегрируя, имеем , , откуда . Следовательно, . Теперь можно найти общее решение данного уравнения . Найдем частное решение, подставив в уравнения и начальные данные:

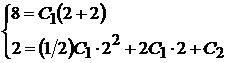Откуда . Таким образом, искомое частное решение имеет вид .n

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида , (*) где постоянные величины.

Для отыскания общего решения уравнения составляется характеристическое уравнение , которое получается из уравнения (*) заменой

на соответствующие степени , причем сама функция у заменяется единицей.

Тогда общее решение дифференциального уравнения (*) строится в зависимости от корней r₁ и r₂ характеристического уравнения. Здесь возможны три случая.

I случай. Корни r₁ и r₂ - действительные и различные. В этом случае общее решение уравнения (*) имеет вид

(**)

II случай. Корни r₁ и r₂ - действительные и равные. В этом случае общее решение уравнения (*) имеет вид

(***)

III случай. Корни r₁ и r₂ - комплексно-сопряженные: и . В этом случае общее решение уравнения (*) имеет вид

(****)

Примеры решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами.

1. Решить уравнение . ¨ Составим характеристическое уравнение и найдем его корни: ; . Так как корни характеристического уравнения действительные и различные, то общее решение данного дифференциального уравнения согласно формуле (**) запишется так: n

2. Решить уравнение . ¨ Составим характеристическое уравнение и найдем его корни: ; . Характеристическое уравнение имеет равные действительные корни; поэтому согласно формуле (***) общее решение данного дифференциального уравнения записывается в виде n

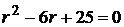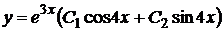3. Решить уравнение . ¨ составим характеристическое уравнение и найдем его корни: ; , здесь .Так как характеристическое уравнение имеет два комплексно-сопряженных корня, то общее решение дифференциального уравнения согласно формуле (****) записывается в виде n

Основы численных методов

Вопросы к теме

1. Абсолютная и относительная погрешности.

2. Округление чисел. Погрешности простейших арифметических действий

Краткие теоретические сведения

Приближенные значения величины

В процессе решения задач вычислитель сталкивается с различными числами, которые могут быть точными или приближенными. Точные числа дают истинное значение величины числа, приближенные – близкое к истинному, причем степень близости определяется погрешностью вычисления.

Например, в утверждениях: «на руке 5 пальцев», «в группе 32 студента», «куб имеет 6 граней» числа 5, 32, 6 – точные. В утверждениях: «ширина дома 14, 25 мм», «вес коробки 50 г», «в лесу около 5000 деревьев» числа 14,25; 50, 5000 – приближенные. Измерение ширины дома производится измерительными средствами, которые сами могут быть неточными; кроме того, измеритель при измерении допускает ошибку (погрешность). При взвешивании коробки также допускается ошибка, так как автоматические весы не чувствительны к увеличению или уменьшению веса на 0,5 г. Произвести точно подсчет количества деревьев в лесу невозможно, так как некоторые деревья могут быть подсчитаны дважды; другие совсем не включались в счет; некоторые деревья были отнесены к кустарникам и исключены из счета, и, наоборот, кустарники включены в счет количества деревьев.

Во многих случаях жизни невозможно найти точное значение величины числа и вычислителю приходится довольствоваться его приближенным значением. Кроме того, очень часто вычислитель сознательно заменяет точное значение приближенным в целях упрощения вычислений.

Таким образом, приближенным числом называется число, незначительно отличающееся от точного числа и заменяющее последнее в вычислениях.

Абсолютная погрешность

При решении той или иной задачи мы получаем числовой результат, который, как правило, не является точным, так как при постановке задачи и в ходе вычислений возникают погрешности.

Если , то говорят, что число является приближенным значением числа по недостатку; если - приближенным значением по избытку. Разность между точным числом и его приближенным значением составляет ошибку, или погрешность. Если , то ; если , то . Как правило, знак ошибки вычислителя не интересует, поэтому пользуются абсолютной погрешностью.

Модуль (абсолютная величина) разности между точным числом и его приближенным значением называется абсолютной погрешностью приближенного числа : .

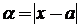Число называется приближенным значением точного числа с точность до , т.е. . Число называется границей абсолютной погрешности (или предельной абсолютной погрешностью) приближенного числа . Существует бесконечное множество чисел , удовлетворяющих приведенному определению; поэтому на практике стараются подобрать, возможно меньшее и простое по записи число .

По известной границе абсолютной погрешности находят границы, в которых заключено точное значение числа : .

Пример 1. Даны приближенные значения числа 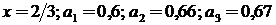. Какое из этих трех приближений является лучшим?

Находим:

Лучшим приближением числа является .

Пример 2. Длина детали (см) заключена в границах 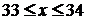. Найти границу абсолютной погрешности измерения детали.

Примем за приближенное значение длины детали среднее арифметическое границ: 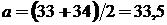(см). Тогда граница абсолютной погрешности приближенного значения длины детали не превзойдет (см). Величину можно найти и как полуразность верхней и нижней границ, т.е. . Длина детали , найденная с точностью до 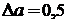(см), заключена между приближенными значениями числа :

(см).

На практике часто применяют выражение типа: «с точностью до »; «с точностью до см» и т.д. Это означает, что граница абсолютной погрешности соответственно равна см и т.д.

Цифра приближенного числа называется верной в широком смысле, если граница абсолютной погрешности числа не превосходит единицы того разряда, в котором записывается цифра .

Цифра приближенного числа называется верной в строгом смысле, если граница абсолютной погрешности числа не превосходит половины единицы того разряда, в котором записана цифра .

В числах, полученных в результате измерений или вычислений и используемых при расчетах в качестве исходных данных, а так же в десятичной записи приближенного значения числа, все цифры должны быть верными.

Наиболее употребительна такая запись приближенного числа (например, в математических таблицах), при которой цифры верны в строгом смысле.

Граница абсолютной погрешности находится непосредственно по записи приближенного значения числа .

Цифры в записи приближенного числа, о которых неизвестно, являются ли они верными, называются сомнительными.

Значащими цифрами приближенного числа называются все его верные цифры, кроме нулей, стоящих перед первой цифрой (слева направо), отличной от нуля.

При округлении числа его заменяют числом с меньшим количеством значащих цифр. Абсолютная величина разности называется погрешностью округления.

При округлении числа до значащих цифр отбрасываются все цифры, стоящие правее -й значащей цифры, или при сохранении разрядов заменяют их нулями. При этом если первая слева из отброшенных цифр больше или равна 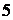, то последнюю оставшуюся цифру увеличивают на единицу.

При применении этого правила погрешность округления не превосходит половины единицы десятичного разряда, определяемого последней оставленной значащей цифрой.

Округление приближенных значений чисел с сохранением в записи только верных цифр производится до разряда, в котором записана первая справа верная цифра

Пример 1. Найти границу абсолютной погрешности приближенного значения числа , все цифры которого верны в строгом смысле.

Граница абсолютной погрешности этого числа равна , т.е. половине единицы последнего разряда, сохраняемого в записи.

Пример 2. Указать верные цифры (в широком смысле) следующих чисел:

1) . Граница погрешности не превосходит единицы разряда десятых (неравенство верное). Следовательно, верными являются цифры и .

2) . Так как , то все цифры приближенного числа 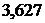верны.

3) 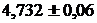. Так как , верными являются цифры и .

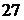Пример 3. За приближенное значение числа взято число . Являются ли цифры числа 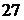верными?

Так как , то цифры и – верные в строгом смысле.

Пример 4. Приближенное значение числа округлить до первого справа верного разряда.

Первая справа верная цифра находится в разряде десятых, поэтому число округляем до десятых: . Новое значение границы погрешности равно сумме границы погрешности и погрешности округления , т.е. . Число является приближенным значением числа с точностью до . Цифры и верные.

Для того чтобы определить качество произведенных измерений, необходимо определить, какую долю составляет абсолютная или предельная абсолютная погрешность от измеряемой величины. В связи с этим вводится понятие относительной погрешности.

Относительная погрешность

Относительной погрешностью приближенного значения числа называется отношение абсолютной погрешности этого приближения к числу , т.е. .

Так как абсолютная погрешность обычно бывает, неизвестна, то на практике оценивают модуль относительной погрешности некоторым числом , которое заведомо меньше этого модуля: . Число называется границей относительной погрешности.

Границей относительной погрешности приближенного значения называется отношение границы абсолютной погрешности к модулю числа : .

Чем меньше относительная погрешность, тем выше качество измерений или вычислений. Относительная погрешность – величина безразмерная, что позволяет сравнивать качество измерений величин разной размерности.

Зависимость относительной погрешности от числа значащих цифр иллюстрируется таблицей:

Число	Наименьшее число	Наибольшее число	Граница абсолютной погрешности	Относительная погрешность наибольшего числа	Относительна погрешность наименьшего числа
Однозначное	1	9	0,5	0,056=5,6%	0,5=50%
Двузначное	10	99	0,5	0,005=0,5%	0,05=5%
Трехзначное	100	999	0,5	0,0005=0,05%	0,005=0,5%
Четырехзначное	1000	9999	0,5	0,00005=0,005%	0,0005=0,05%

В ряде задач границу абсолютной погрешности находят по данной относительной погрешности и модулю приближенного значения величины: .

Пример 1. В результате измерений получили, что длина карандаша равна см, а длина комнаты равна см. Что можно сказать о качестве этих двух измерений?

(при измерении длины карандаша);

(при измерении длины комнаты).

Следовательно, качество измерения длины комнаты значительно выше, чем качество измерений длины карандаша.

Пример 2. Найти относительную погрешность числа , если обе цифры его верны в строгом смысле.

По условию, ; поэтому .

Пример 3. Какие цифры числа являются верными?

По формуле находим . Верными являются первые две цифры: и .

Пример 4. При вычислении некоторой величины стало известно, что . Сколько верных цифр нужно взять, чтобы приближенное значение имело относительную погрешность не больше ?

Чтобы значение было наибольшим, примем . По формуле получим . Следовательно, нужно взять две верные цифры.

Погрешности арифметических действий

Граница абсолютной погрешности суммы приближенных значений чисел равна сумме границ абсолютных погрешностей этих чисел: , где и - приближенные значения чисел; и - границы абсолютных погрешностей соответствующих приближений.

Граница относительной погрешности суммы вычисляется по формуле .

Пример. Найти сумму приближенных значений чисел и .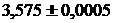

Имеем .

Граница абсолютной погрешности заключена в пределах . В приближенном значении суммы верными являются лишь две цифры (в разрядах десятков и единиц). Полученный результат округлим до единиц: .

Граница абсолютной погрешности разности двух приближенных значений чисел равна сумме границ их абсолютных погрешностей: . Граница относительной погрешности разности вычисляется по формуле .

Пример. Вычислить разность двух приближенных значений чисел и . Найти и . Вычисляем границу абсолютной погрешности разности . В приближенном значении разности цифра в разряде тысячных не может быть верной, так как . Итак, 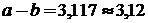все цифры верные.

Находим относительную погрешность разности: .

Формулы для оценки границ абсолютной погрешности произведения (частного) сложны, поэтому на практике сначала находят относительную погрешность произведения (частного), а затем границу абсолютной погрешности произведения (частного). Формулы для границ абсолютной и относительной погрешностей некоторых функций приведены в таблице:

№ п/п	Функции	Граница абсолютной погрешности	Граница относительной погрешности
1.
2.
3.
4.
5.
6.
7.
8.

Пример 1. Найти верные цифры произведения приближенных значений чисел и .

Имеем . Границы абсолютной погрешности сомножителей равны и . По формуле 1. находим относительную погрешность произведения: . Находим границу абсолютной погрешности произведения: . Полученный результат означает, что в произведении одна верная цифра (в разряде десятых): .

Пример 2. Найти границу абсолютной погрешности частного приближенных значений чисел 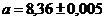и .

Имеем . По формуле 8. находим относительную погрешность частного . Находим границу абсолютной погрешности частного: . Полученный результат означает, что в частном все три цифры верные.

Пример 3. Вычислить относительную погрешность, допущенную при вычислении площади квадрата, если приближенное значение стороны квадрата равно .

По формуле 4. получим .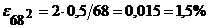

Пример 4. Вычислить относительную погрешность, допущенную при извлечении квадратного корня из числа .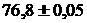

По формуле 6. получим .

Пример 5. Вычислить границу абсолютной погрешности при нахождении гипотенузы прямоугольного треугольника, катеты которого равны см и см.

Имеем см. По формулам 6. и 8. находим границу абсолютной погрешности:

см

Таким образом, см Верными являются первые две значащие цифры и .

ОСНОВЫ ДИСКРЕТНОЙ МАТЕМАТИКИ

Вопросы к теме

1. Основы теории множеств.

2. Элементы математической логики.

Краткие теоретические сведения

Основы теории множеств

Понятие множества принадлежит к числу фундаментальных неопределяемых понятий математики. Можно сказать, что множество – это любая определенная совокупность объектов. Объекты, из которых составлено множество, называются его элементами. Элементы множества различны и отличимы друг от друга.

Пример: Множество S страниц в данной методичке. Множество натуральных чисел Множество простых чисел Множество целых чисел: Множество Rвещественных чисел. Множество A различных символов на этой странице.

Если объект является элементом множества , то говорят, что (Обозначение: ). В противном случае говорят, что 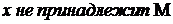(Обозначение: ).

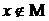Множества, как объекты, могут быть элементами других множеств. Множество, элементами которого являются множества, обычно называется классом или семейством.

Множество, не содержащее элементов, называется пустым.

Обозначение:

Чтобы задать множество, нужно указать, какие элементы ему принадлежат.

Это можно сделать различными способами:

перечисление элементов: (обозначения элементов обычно заключают в фигурные скобки и разделяются запятыми);

характеристическим предикатом: 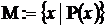(это некоторое условие, выраженное в форме логического утверждения или процедуры, возвращающей логическое значение: если для данного элемента условие выполнено, то он принадлежит определенному множеству, в противном случае – не принадлежит);

порождающей процедурой: (процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определяемого множества).

Примеры: 1. ;

2. &

Перечислением можно задавать только конечные множества. Бесконечные множества задаются характеристическим предикатом или порождающей процедурой.

Множество целых чисел в диапазоне от m до n обозначается так: m…n. То есть ;

Множество A содержится в множестве B (множество B включает множество A), если каждый элемент A есть элемент B: .

В этом случае называется подмножеством , - надмножеством . Если и , то называется собственным подмножеством .

Два множества равны, если они являются подмножествами друг друга: & .

Мощностью множества обозначатся . Для конечных множеств мощность – это число элементов. Если , то множества и называются равномощными.

Операции над множествами:

- объединение: ;

- персечение: & ;

- разность: & ;

- симметрическаяразность:

- дополнение: .

Операция дополнения подразумевает универсум .

Пример: Пусть .

Тогда

Диаграммы Эйлера, иллюстрируют операции над множествами. Сами исходные множества изображаются фигурами (в данном случае овалами), а результат графически выделяется (в данном случае для выделения использована штриховка).

Свойства операций над множествами:

Пусть задан универсум . Тогда 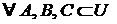выполняются следующие свойства.

1. идемпотентность: ;

2. коммутативность: ;

3. ассоциативность: ;

4. дистрибутивность:

5. поглощение: ;

6. свойство нуля: ;

7. свойство единицы: ;

8. инволютивность: ;

9. законы Моргана: ;

10. свойства дополнения: ;

11. выражение для разности: .

В справедливости перечисленных свойств можно убедиться различными способами. Например, нарисовать диаграммы Эйлера для левой и правой частей равенства, и убедится, что они совпадают.

Элементы математической логики (алгебры логики)

Алгебра в широком смысле этого слова – наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над различными математическими объектами (алгебра функций, алгебра векторов и так далее). Объектами алгебры логики являются высказывания.

Высказывание – это форма мышления, выраженная с помощью понятий, посредством которой что-либо утверждают или отрицают о предметах, их свойствах и отношениях между ними.

О предметах можно судить верно или неверно, то есть высказывание может быть истинным (обозначается 1) или ложным (обозначается 0).

Высказывание называется простым, если никакая его часть сама не является высказыванием. Высказывание, состоящее из простых высказываний, называется составным (сложным).

Например, А = {Аристотель – основоположник логики}

              В = {Лондон – столица Парижа}

Таким образом, А = 1, В = 0.

Составные высказывания на естественном языке образуются с помощью союзов, которые в алгебре логики заменяются на логические операции. Логические операции задаются таблицами истинности и могут быть графически проиллюстрированы с помощью диаграмм Эйлера-Венна.

Логические операции

1. Конъюнкция (логическое умножение)

· в естественном языке соответствует союзу И;

· обозначается & или

Конъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Диаграмма Эйлера-Венна       соответствует пересечению множеств.

Таблица истинности

А В А&В

0 0 0

0 1 0

1 0 0

1 1 1

2. Дизъюнкция (логическое сложение)

· в естественном языке соответствует союзу ИЛИ;

· обозначается

Дизъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.

Диаграмма Эйлера-Венна       соответствует объединению множеств.

Таблица истинности

А В А В

0 0 0

0 1 1

1 0 1

1 1 1

3. Инверсия (отрицание)

· в естественном языке соответствует словам НЕВЕРНО, ЧТО… и частице НЕ;

· обозначается

Инверсия – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.

Таблица истинности

А

0 1

1 0

Диаграмма Эйлера-Венна

4. Импликация (логическое следование)

· в естественном языке соответствует обороту ЕСЛИ …, ТО…

· обозначение

Импликация – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

Таблица истинности

А В А В

0 0 1

0 1 1

1 0 0

1 1 1

5. Эквиваленция (равнозначность)

· в естественном языке соответствует обороту ТОГДА И ТОЛЬКО ТОГДА, КОГДА…

· обозначение

Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.

Таблица истинности

А В А В

0 0 1

0 1 0

1 0 0

1 1 1

Последовательности и ряды

Вопросы к теме

1. Числовые ряды Знакопеременные ряды.

2. Степенные ряды.

3. Признаки сходимости ряда

Краткие теоретические сведения

Числовым рядом называется сумма вида 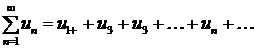, где числа , называемые членами ряда, образуют бесконечную последовательность; член 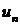называется общим членом ряда.

Суммы









Составленные из первых членов ряда, называются частными суммами этого ряда.

Каждому ряду можно сопоставить последовательность частичных сумм . Если при бесконечном возрастании номера частичная сумма ряда стремится к пределу , то ряд называется сходящимся, а число - суммой сходящегося ряда, т.е. или . Эта запись равносильна записи .

Если частичная сумма ряда при неограниченном возрастании не имеет конечного предела (в частности, стремится к или ), то такой ряд называется расходящимся.

Если ряд сходится, то значение при достаточно большом является приближенным выражением суммы ряда .

Разность называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е. , и наоборот, если остаток стремится к нулю, то ряд сходится.

Пример: записать ряд по его заданному общему члену .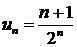

Полагая , имеет бесконечную последовательность чисел: . Сложив ее члены, получим ряд .

Пример: записать ряд по его заданному общему члену .

Полагая , имеет бесконечную последовательность чисел: . Сложив ее члены, получим ряд .

Пример: записать ряд по его заданному общему члену .

Полагая и учитывая, что , получим ряд .

Пример: найти - й член ряда по его данным первым членам .

Знаменатели членов ряда, начиная с третьего, являются нечетными числами; следовательно, - й член ряда имеет вид .

Пример: найти - й член ряда по его данным первым членам .

Числители членов ряда представляют собой квадратные корни из натуральных чисел, а их соответствующие знаменатели равны 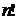. Знаки чередуются по закону . Общий член ряда имеет вид .

Пример: найти - й член ряда по его данным первым членам .

Числители членов ряда образуют натуральный ряд чисел, а соответствующие им знаменатели – натуральный ряд чисел, начиная с . Знаки чередуются по закону 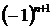или по закону 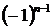. Значит - й член ряда имеет вид или .

Пример: найти сумму членов ряда .

Находим частичные суммы членов ряда:

Запишем последовательность частичных сумм: . Общий член этой последовательности есть . Следовательно, . Последовательность частичных сумм имеет предел, равный . Итак, ряд сходится и его сумма равна .

Необходимый признак сходимости ряда

Ряд 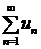может сходится только при условии, что его общий член 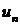при неограниченном увеличении номера стремится к нулю: .

Если , то ряд 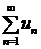расходится – это достаточный признак расходимости ряда.

Пример: Исследовать сходимость ряда, применяя необходимый признак сходимости .

Находим . Необходимый признак сходимости ряда выполняется.

Пример: Исследовать сходимость ряда, применяя необходимый признак сходимости .

Имеем . Здесь выполняется достаточный признак расходимости ряда; следовательно, ряд расходится.

Пример: Исследовать сходимость ряда, применяя необходимый признак сходимости .

Находим . Необходимый признак сходимости ряда выполняется.

Достаточный признак сходимости ряда с положительными членами

Признак Даламбера:Если для ряда с положительными членами выполняется условие 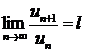, то ряд сходится при и расходится при .

Признак Даламбера не дает ответа, если 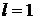. В этом случае для исследования применяются другие приемы.

Пример: Исследовать сходимость ряда, используя признак Даламбера

Подставив в общий член ряда вместо n число n+1, получим . Найдем предел отношения (n+1)–го члена к n–му члену при n :

. Следовательно, данный ряд сходится.

Числовые последовательности

Под числовой последовательностью понимается функция заданная на множестве натуральных чисел. Кратко последовательность обозначается в виде или . Число называется первым членом (элементом) последовательности, - вторым, …, - общим или -м членом последовательности.

Чаще всего последовательность задается формулой его общего члена. Формула позволяет вычислить любой член последовательности по номеру .

Так, равенства

Задают соответственно последовательности





    Последовательность называется ограниченной, если существует такое число , что для любого выполняется неравенство . В противном случае последовательность называется неограниченной. Легко видеть, что последовательности и 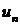ограничены, а 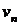и - неограниченны.

Последовательность называется возрастающей (неубывающей), если для любого выполняется неравенство . Аналогично определяется убывающая (невозрастающая) последовательность.

Все эти последовательности называются монотонными последовательностями. Последовательност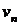и , и 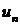монотонные, а - не монотонная.

Если все элементы последовательности равны одному и тому же числу , то ее называют постоянной.

Другой способ задания числовых последовательностей – рекуррентный способ. В нем задается начальный элемент (первый член последовательности) и правило определения -го элемента по -му: . Таким образом, , и т.д. При таком способе задания последовательности для определения -го члена надо сначала посчитать все предыдущих.

Степенные ряды

Степенным рядом называется ряд вида , где числа называются коэффициентами ряда, а член - общим членом ряда.

Областью сходимости степенного ряда называется множество всех значений , при которых данный ряд сходится.

Число называется радиусомсходимости степенного ряда, если при ряд сходится и при том абсолютно, а при ряд расходится.

Если существует предел , то радиус сходимости ряда равен этому пределу и степенной ряд сходится при , т.е. в промежутке , который называется промежутком (интервалом) сходимости.

Если предел равен нулю , то степенной ряд сходится в единственной точке .

На концах промежутка ряд может сходиться (абсолютно или условно), но может и расходится. Сходимость степенного ряда при и исследуется с помощью какого-либо из признаков сходимости.

Пример: дан ряд . Исследовать его сходимость в точках .

При 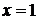данный ряд превращается в числовой ряд . Исследуем сходимость этого ряда по признаку Даламбера. Имеем ;

, т.е. ряд сходится.

При получим ряд 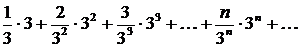или , который расходится, так как не выполняется необходимый признак сходимости ряда .

Дата добавления: 2018-02-28; просмотров: 300; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!