Интегральное исчисление. Неопределенный интеграл
Nbsp; Колледж экономики, права и информационных технологий Конспект лекций по дисциплине
МАТЕМАТИКА
(избранные главы)
для специальности
40.02.01 Право и организация социального обеспечения
Мурманск
2017
Оглавление
Предел функции.. 4
Элементы комбинаторики.. 8
Элементы теории вероятностей.. 12
Дифференциальное исчисление.. 18
Интегральное исчисление. Неопределенный интеграл.. 24
Обыкновенные дифференциальные уравнения.. 34
Основы численных методов.. 39
ОСНОВЫ ДИСКРЕТНОЙ МАТЕМАТИКИ.. 45
Последовательности и ряды... 50
Предел функции
Вопросы к теме
1. Понятие предела функции. Свойства бесконечно больших и бесконечно малых функций. Теоремы о пределах.
2. Вычисления предела с неопределённостями типа 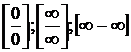 .
.
Краткие теоретические сведения
Число А называется пределом функции 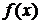 при
при 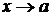 , если для любого
, если для любого 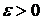 можно указать такое
можно указать такое 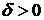 , что для любого
, что для любого 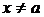 , удовлетворяющего неравенству
, удовлетворяющего неравенству 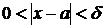 , выполняется неравенство
, выполняется неравенство 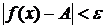 .
.
В этом случае пишут 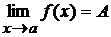 .
.
Функция 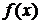 называется бесконечно малой при
называется бесконечно малой при 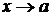 , если
, если 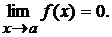
Функция 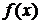 называется бесконечно большой при
называется бесконечно большой при 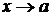 , если
, если 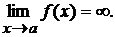
Свойства бесконечно малых и бесконечно больших функций:
10. Если 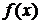 и
и 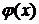 - бесконечно малые при
- бесконечно малые при 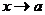 , то их сумма
, то их сумма 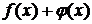 при
при 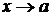 также является бесконечно малой.
также является бесконечно малой.
20. Если 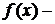 бесконечно малая функция при
бесконечно малая функция при 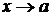 , а
, а 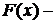 ограниченная функция, то их произведение
ограниченная функция, то их произведение 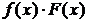 есть функция бесконечно малая.
есть функция бесконечно малая.
|
|
|
30. Если при 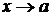 функция
функция 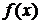 имеет конечный предел, а функция
имеет конечный предел, а функция 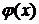 - бесконечно большая, то
- бесконечно большая, то 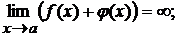
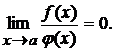
40. Если 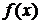 - бесконечно малая функция при
- бесконечно малая функция при 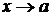 , то функция
, то функция 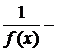 бесконечно большая и наоборот.
бесконечно большая и наоборот.
Теоремы о пределах:
Теорема 1. Если существуют пределы 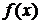 и
и 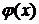 при
при 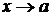 , то существует также и предел их суммы, равный сумме пределов функций
, то существует также и предел их суммы, равный сумме пределов функций 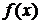 и
и 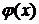 .
.
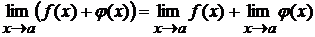
Теорема 2. Если существуют пределы 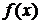 и
и 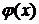 при
при 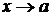 , то существует также и предел их произведения, равный произведению пределов функций
, то существует также и предел их произведения, равный произведению пределов функций 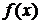 и
и 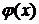 .
.
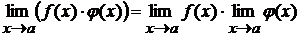
Теорема 3. Если существуют пределы 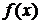 и
и 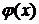 при
при 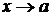 и
и 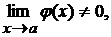 то существует также и предел отношения, равный отношению пределов функций
то существует также и предел отношения, равный отношению пределов функций 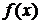 и
и 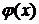 .
.
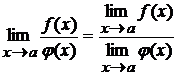 .
.
Следствие 1. Постоянный множитель можно вынести за знак предела:
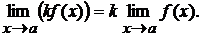
Следствие 2. Если 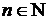 , то
, то 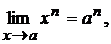
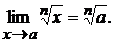
Следствие 3. Предел многочлена (целой рациональной функции) 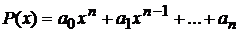 при
при 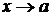 равен значению этого многочлена при
равен значению этого многочлена при 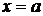 , т.е.
, т.е. 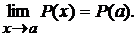
Следствие 4. Предел дробно-рациональной функции
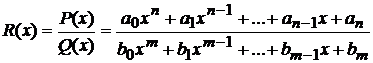
при 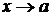 равен значению этой функции при
равен значению этой функции при 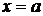 , если
, если  принадлежит области определения функции, т.е.
принадлежит области определения функции, т.е. 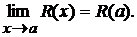
Рассмотрим некоторые примеры.
Вычислить пределы:
1.1. 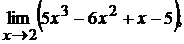 1.2.
1.2. 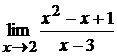 .
.
£ 1.1. По правилу нахождения предела многочлена находим
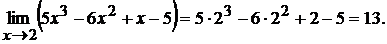
1.2.Так как при 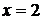 знаменатель дроби отличен от нуля, то по правилу нахождения предела дробно-рациональной функции получим
знаменатель дроби отличен от нуля, то по правилу нахождения предела дробно-рациональной функции получим
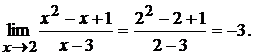 ¢
¢
|
|
|
2.1. 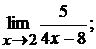 2.2.
2.2. 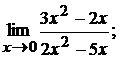 2.3.
2.3. 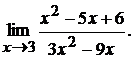
£ 2.1. Здесь предел делителя равен нулю: 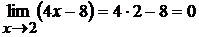 . Следовательно, теорему о пределе частного применить нельзя. Так как
. Следовательно, теорему о пределе частного применить нельзя. Так как 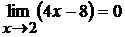 , то
, то 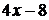 при
при 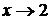 есть величина бесконечно малая, а обратная ей величина
есть величина бесконечно малая, а обратная ей величина 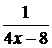 – бесконечно большая. Поэтому при
– бесконечно большая. Поэтому при 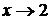 произведение
произведение 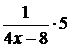 есть величина бесконечно большая, т.е.
есть величина бесконечно большая, т.е. 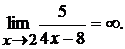
2.2. Здесь пределы числителя при 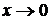 равны нулю. Непосредственной подстановкой вместо аргумента его предельного значения вычислить предел нельзя, так как при
равны нулю. Непосредственной подстановкой вместо аргумента его предельного значения вычислить предел нельзя, так как при 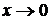 получается отношение двух бесконечно малых величин.
получается отношение двух бесконечно малых величин.
Разложим числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю, и, следовательно, сделать возможным применение теоремы 3. Нужно иметь в виду, что здесь не производится сокращение на нуль, что недопустимо. По определению предела функции аргумент  стремится к своему предельному значению, никогда не принимая этого значения; поэтому до перехода к пределу можно произвести сокращение на множитель, стремящийся к нулю. Имеем
стремится к своему предельному значению, никогда не принимая этого значения; поэтому до перехода к пределу можно произвести сокращение на множитель, стремящийся к нулю. Имеем
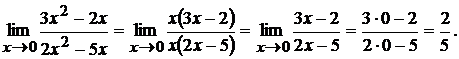
2.3. Пределы числителя и знаменателя при 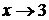 равны нулю:
равны нулю: 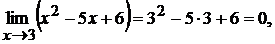
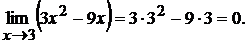 Разложим квадратный трехчлен в числители на линейные множители по формуле
Разложим квадратный трехчлен в числители на линейные множители по формуле 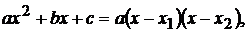 где
где 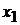 и
и 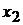 – корни трехчлена. Разложив на множители знаменатель, сократим дробь на
– корни трехчлена. Разложив на множители знаменатель, сократим дробь на 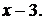 Используя следствие 4, получим
Используя следствие 4, получим 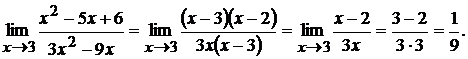 ¢
¢
|
|
|
3.1. 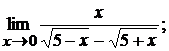 3.2.
3.2. 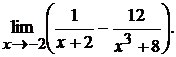
£ 3.1. Пределы числителя и знаменателя при 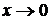 равны нулю. Умножив числитель и знаменатель на сопряженный знаменателю множитель
равны нулю. Умножив числитель и знаменатель на сопряженный знаменателю множитель 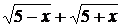 и затем сократив дробь на
и затем сократив дробь на  , получим
, получим


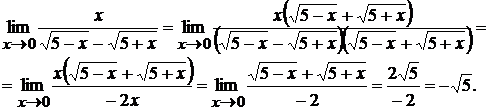
3.2. Очевидно, что при 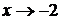 функция представляет собой разность двух бесконечно больших величин. Выполнив вычитание дробей, получим дробь, числитель и знаменатель которой при
функция представляет собой разность двух бесконечно больших величин. Выполнив вычитание дробей, получим дробь, числитель и знаменатель которой при 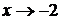 стремится к нулю. Сократив дробь на
стремится к нулю. Сократив дробь на 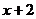 , находим
, находим
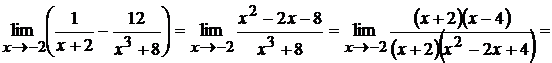
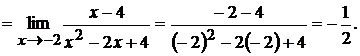 ¢
¢
4.1. 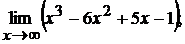 4.2.
4.2. 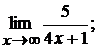
4.3. 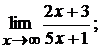 4.4.
4.4. 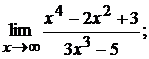 4.5.
4.5. 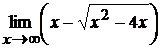
£ 4.1. Первые три слагаемых при  пределов не имеют, поэтому следствием 3 непосредственно воспользоваться нельзя. Вынося
пределов не имеют, поэтому следствием 3 непосредственно воспользоваться нельзя. Вынося 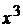 за скобки, получим
за скобки, получим
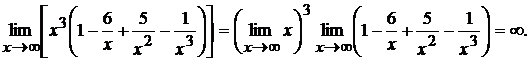
(при  величины
величины 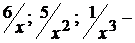 бесконечно малые и их пределы равны нулю).
бесконечно малые и их пределы равны нулю).
При  знаменатель
знаменатель 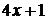 неограниченно растет, т.е. является величиной бесконечно большой, а обратная величина
неограниченно растет, т.е. является величиной бесконечно большой, а обратная величина 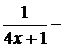 бесконечно малой. Произведение
бесконечно малой. Произведение 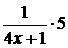 бесконечно малой на ограниченную величину (постоянная – частный случай ограниченной величины) есть величина бесконечно малая, и предел ее при
бесконечно малой на ограниченную величину (постоянная – частный случай ограниченной величины) есть величина бесконечно малая, и предел ее при  равен нулю. Следовательно,
равен нулю. Следовательно, 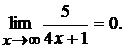
4.3. При  числитель и знаменатель – величины бесконечно большие. Поэтому при непосредственном применении теоремы 3 получаем выражение
числитель и знаменатель – величины бесконечно большие. Поэтому при непосредственном применении теоремы 3 получаем выражение 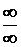 , которое представляет собой неопределенность. Для вычисления предела этой функции нужно числитель и знаменатель разделить на
, которое представляет собой неопределенность. Для вычисления предела этой функции нужно числитель и знаменатель разделить на  :
:
|
|
|
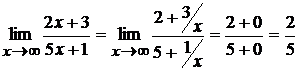 (при
(при  слагаемые
слагаемые 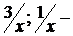 величины бесконечно малые и, следовательно, их пределы равны нулю).
величины бесконечно малые и, следовательно, их пределы равны нулю).
4.4. Разделим числитель и знаменатель на наивысшую степень аргумента в знаменателе, т.е. на 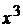 :
: 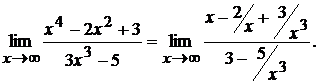
При  имеем
имеем 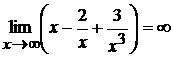 и
и 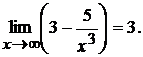
Так как знаменатель есть величина ограниченная, то 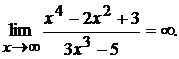
4.5. При  данная функция представляет собой разность двух бесконечно больших величин
данная функция представляет собой разность двух бесконечно больших величин 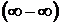 . Умножив и разделив функцию на выражение
. Умножив и разделив функцию на выражение 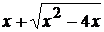 , получим
, получим
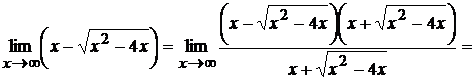
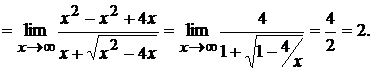 ¢
¢
Элементы комбинаторики
Вопросы к теме
1. Множества. Подмножества.
2. Понятие комбинаторики. Правила суммы и произведения.
3. Формулы комбинаторики: перестановки без повторений, размещения без повторений, сочетания.
Краткие теоретические сведения
Одним из фундаментальных, неопределяемых математических понятий является понятие множества. Множество можно представить себе как совокупность некоторых объектов, объединенных по одному какому-либо признаку (множество четных чисел, множество цветов спектра, множество букв русского алфавита).
Теория множеств создана великим немецким математиком Георгом Кантором. Главная заслуга Кантора состоит в признании того факта, что бесконечность – это не абстракция, придуманная философами, а реальность; что бесконечные совокупности предметов существуют наравне с конечными. В самом деле, легко построить прямоугольный треугольник с единичными катетами. По теореме Пифагора его гипотенуза равна 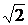 , т.е. иррациональному числу, десятичное разложение которого бесконечно и не содержит периода.
, т.е. иррациональному числу, десятичное разложение которого бесконечно и не содержит периода.
Кантор описывает множество следующим образом: «Множество  есть любое собрание определенных и различимых между собой объектов нашей интуиции и интеллекта, мыслимое как единое целое. Эти объекты называются элементами множества
есть любое собрание определенных и различимых между собой объектов нашей интуиции и интеллекта, мыслимое как единое целое. Эти объекты называются элементами множества  ».
».
Предметы (объекты), из которых составлено множество, называются элементами множества.
Если все элементы множества А являются в то же время элементами множества В, то множество А называется подмножеством множества В.
Студент должен понимать, что такое множество, уметь привести примеры, объяснить что означает конечное, бесконечное и пустое множество.
На практике часто приходится выбирать из некоторого множества объектов подмножества элементов, обладающих определенными свойствами, располагать элементы множества в каком-то определенном порядке, подсчитывать число всех возможных способов расположения некоторых предметов.
Так учителю приходится распределять некоторые различные виды работ между учащимися (или оценки); лингвисту – выбирать порядок слов в предложении; шахматисту – из нескольких серий ходов выбирать наилучшую.
В практической деятельности юристу часто приходится иметь дело с самыми разнообразными ситуациями. Умение анализировать сложившуюся обстановку, адекватно ее оценивать и делать правильные выводы является важным качеством каждого профессионала.
Задачи такого типа называются комбинаторными, поскольку в них речь идет о некоторых комбинациях работ, слов, ходов.
Область математики, в которой изучаются комбинаторные задачи называется комбинаторикой.
Другими словами, комбинаторика изучает количество комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества (конечные множества содержат конечное число элементов).
Комбинаторные задачи связаны: а) с выбором из некоторого множества элементов те, которые обладают заданными свойствами; б) с расположением этих элементов в определенном порядке; в) с расчетом числа возможных комбинаций.
Решение большинства комбинаторных задач основано на двух простых правилах: суммы и произведения.
Правило суммы. Пусть из множества А элемент 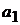 можно выбрать
можно выбрать 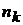 способами, элемент
способами, элемент 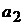 -
- 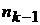 способом и т.д., элемент
способом и т.д., элемент 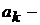 одним способом, отличными от предыдущих. Тогда выбор одного из элементов
одним способом, отличными от предыдущих. Тогда выбор одного из элементов 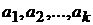 можно произвести
можно произвести 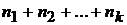 способами.
способами.
Пример 1. Пусть в корзине имеется 7 апельсинов, 5 бананов и 10 яблок. Тогда выбор одного из фруктов можно сделать 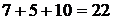 способами.
способами.
Правило произведения. Пусть А – некоторое множество, из которого выбор элемента 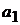 можно осуществить
можно осуществить 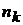 способами,
способами, 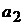 -
- 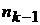 способом и т.д.,
способом и т.д., 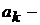 одним способом. Тогда одновременный выбор элементов
одним способом. Тогда одновременный выбор элементов 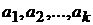 в указанном порядке можно осуществить
в указанном порядке можно осуществить 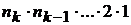 способом.
способом.
Пример 2. Пусть в велосипеде имеются 3 ведущие звездочки и 4 ведомые. Сколько передач имеется в велосипеде? £ Так как каждая передача определяется выбором одной ведущей и одной ведомой, то число всех передач совпадает с числом выборов одного элемента из 3 и другого элемента из 4. Поэтому 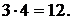 ¢
¢
Пример 3. Имеется 5 стульев и 2 студента. Сколькими способами можно посадить этих студентов на стулья? £ Первого студента можно посадить на стул пятью способами, а второго – четырьмя, т.к. один стул уже занят. Всего будет 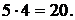 ¢
¢
Рассмотрим наиболее употребительные формулы комбинаторики, которые используются при решении задач по теории вероятностей.
Перестановки без повторений
Перестановками без повторений называют комбинации, состоящие из одних и тех же  различных элементов и отличающиеся только порядком их расположения.
различных элементов и отличающиеся только порядком их расположения.
Произведение  натуральных чисел называют «
натуральных чисел называют « 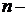 факториал» и обозначают
факториал» и обозначают 
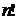
Другими словами, 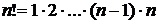 .
.
Например, 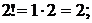
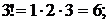
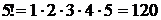 и т.д. Для удобства принято, что
и т.д. Для удобства принято, что 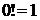 и
и 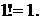
Таким образом, обозначим 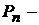 число всех возможных перестановок, тогда
число всех возможных перестановок, тогда 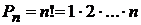 .
.
Пример 4. Из четырех букв: a, b, c, d можно сделать 24 перестановки, так как 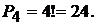 Вот они:
Вот они:
abcd adbc bcda cabd dbac cdab
abdc adcb bcad cadb dbca cdba
acbd bacd bdac cbad dcab dabc
acdb badc bdca cbda dcba dacb
Пример 5. В отделении сержанта Сбруева проходят службу 5 новобранцев: Белкин, Пенкин, Свечкин, Овечкин, Мышкин. В свободное от нарядов время сержант обучает их, как рассчитываться по порядку. Сколько раз может Сбруев повторить это упражнение, используя только разные способы построения солдат?
£ Договоримся указывать порядок расположения солдат первыми буквами их фамилий. Например, БПСОМ, затем ПБСОМ и т.д. Все комбинации отличаются одна от другой порядком букв, значит 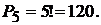 ¢
¢
Размещения без повторений
Размещениями без повторений называют комбинации, составленные из  различных элементов по
различных элементов по  элементов, которые отличаются либо составом элементов, либо их порядком. Обозначают
элементов, которые отличаются либо составом элементов, либо их порядком. Обозначают 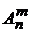 и читают «размещения из
и читают «размещения из  по
по  », причем
», причем 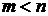 .
.
Число всех возможных размещений: 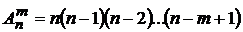 .
.
Отличие этих комбинаций состоит в том, что составление упорядоченного множества заканчивается, когда мы выберем  элементов. Поэтому, чтобы найти число таких упорядоченных подмножеств, нужно перемножить
элементов. Поэтому, чтобы найти число таких упорядоченных подмножеств, нужно перемножить  чисел от
чисел от  до
до 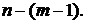
Пример 6. Выбрать 3 краски из имеющихся пяти можно: 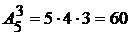 способами.
способами.
Необходимо отметить, что перестановки являются частным случаем размещений.
Таким образом формулу размещений можно переписать иначе: 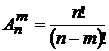 .
.
Пример 7. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2? £ Число таких флажков равно числу размещений из 6 по 2: 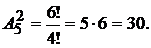 ¢
¢
Сочетания без повторений
Сочетаниями называют комбинации, составленные из  различных элементов по
различных элементов по  элементов, которые отличаются хотя бы одним элементом. Обозначают:
элементов, которые отличаются хотя бы одним элементом. Обозначают: 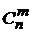 и читают «сочетание из
и читают «сочетание из  по
по  ».
».
Число сочетаний равно: 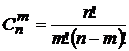 .
.
Замечание. Сочетаниями являются неупорядоченными подмножествами данного множества, то есть в них не важен порядок расположения элементов, поэтому различные сочетания отличаются друг от друга составом элементов.
Свойства.
10. 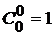 30.
30. 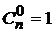 50
50 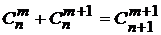
20. 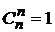 40.
40. 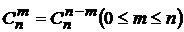
Пример 8. Сколькими способами можно выбрать делегацию в 12 человек из группы в 20 человек? £ порядок следования в делегации не важен, поэтому способов выбора будет:
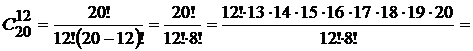
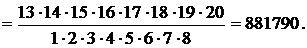 ¢
¢
Пример 9. Сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей? £ 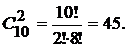 ¢
¢
Студент должен знать основные комбинаторные объекты (типы выборок), формулы и правила расчета количества выборок (для каждого из типа выборок); уметь: определять тип комбинаторного объекта (тип выборок), рассчитывать количество выборок заданного типа в заданных условиях.
Элементы теории вероятностей
Теория вероятностей есть в сущности
не что иное, как здравый смысл, сведенный
к исчислению,… она нас учит
предохранять себя от иллюзий, которые нас
часто сбивают с пути,… нет науки, более
достойной наших размышлений, и… было бы
очень полезно ввести ее в систему
народного образования.
П. Лаплас
Вопросы по теме
1. Испытания. События. Классификация событий.
2. Классическое определение вероятностей.
Краткие теоретические сведения
Трудно найти такую сферу человеческой деятельности, в которой не использовались бы вероятностно-статистические методы. Они применяются практически во всех областях науки, в экономике, военном деле, технике, медицине, юридической практике, криминалистике и т.д. Эти методы базируются на понятиях случайного события и вероятности. Решающий вклад в теорию вероятностей внесли такие замечательные математики как Пьер Ферма, Якоб Бернулли, Симон Лаплас, Пафнутий Чебышев и многие другие.
События взаимосвязаны – одни из них являются следствием (исходом) других и, в свою очередь, служат причиной третьих. Случаен набор выигравших билетов а лотерее, случаен результат встречи двух спортивных команд одного и того же класса и т.п.
Предметом теории вероятностей служит выявление закономерностей, присущих случайным событиям, в абстрактной форме. Главной задачей теории вероятностей является подсчет вероятности случайного события: каждому случайному событию ставится в соответствие число 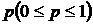 , являющееся мерой его достоверности, мерой того, насколько часто оно происходит.
, являющееся мерой его достоверности, мерой того, насколько часто оно происходит.
В этой науке первыми понятиями служат событие и вероятность.
Всякий раз, когда выполняются определенные условия, говорят, что происходит испытание. Всякий результат или исход испытания называется событием.
Пример 1. Стрелок стреляет по мишени. В данном примере опытом является: выстрел, а событием – попадание в определенную область мишени
Пример 2. В урне имеются цветные шары, из урны наудачу извлекается шар. В данном примере опыт – извлечение шара, а событие – появление шара определенного цвета.
Все наблюдаемые события делят:
ü Достоверные – события, которые обязательно произойдут при каждом испытании. Обозначается: 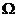 (греческая строчная буква «омега»).
(греческая строчная буква «омега»).
ü Невозможные – события, которые заведомо не произойдут, при одном испытании.
ü Случайные – события, которые могут произойти, а могут и не произойти при осуществлении комплекса условий. Обозначают буквами А, В, С,…
Пример 3. В урне имеются шары только синего и красного цветов. Наугад вынимают один шар. Событие, состоящее в том, что вынут либо синий, либо красный шар – достоверное. Событие, состоящее в том, что вынут шар белого цвета – невозможное. Событие «вынут шар красного цвета» (или событие «вынут шар синего цвета») является случайным.
Виды случайных событий:
ü События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
ü События называются равновозможными, если появление одного из них в результате испытания не является более возможным, чем появление другого.
Пример 4. Игральную кость бросают один раз. События, состоящие из выпадений чисел 1, 2, 3, 4, 5, 6 являются равновозможными.
Пример 5. При однократном бросании монеты выпадает либо орел (событие А), либо решка (событие В). События А и В – несовместные.
Пример 6. Из ящика с деталями наудачу извлечена деталь. Появление стандартной детали исключает появление нестандартной детали. События «появилась стандартная деталь» и «появилась нестандартная деталь» - несовместные.
Каждое испытание можно описать с помощью событий, которые являются несовместными и равновозможными. Эти события называются исходами испытания или элементарными событиями. Совокупность всех исходов испытания называют также пространством элементарных событий или множеством элементарных событий, или полной группой событий (ПГС).
Пример 7. Приобретены два билета денежно-вещевой лотереи. Обязательно произойдет одно и только одно из следующих событий: «выигрыш выпал на первый билет и не выпал на второй», «выигрыш не выпал на первый билет и выпал на второй», «выигрыш выпал на оба билета», «на оба билета выигрыш не выпал». Эти события образуют ПГС.
Пример 8. Стрелок произвел выстрел по цели. Обязательно произойдет одно из следующих двух событий: попадание, промах. Эти два несовместных события образуют ПГС.
Классическое определение вероятности
Как возникла теория вероятностей?
Корни теории вероятностей уходят далеко в глубь веков. Известно, что в древнейших государствах Китае, Индии, Египте, Греции уже использовались некоторые элементы вероятностных рассуждений для переписи населения, и даже определения численности войска неприятеля.
Но все-таки начало теории вероятностей как науки приписывают середине XVII века. Из исторических романов мы помним: это время королей и мушкетеров, прекрасных дам и благородных кавалеров. Как это ни парадоксально, с именем одного из них, причем реального исторического лица, связано начало теории вероятностей.
Следует сразу оговориться, что основоположником теории вероятностей считают великого ученого, математика, физика и философа Блеза Паскаля (1623-1662). Но полагают, что впервые он занялся теорией вероятностей под влиянием вопросов, поставленных перед ним одним из придворных французского двора шевалье де Мере (1607-1648). Блестящий кавалер, умный и развитый человек, де Мере увлекался философией, искусством и ... был азартным игроком! Но игра, оказывается, тоже была для него поводом для довольно глубоких размышлений. Де Мере предложит Б.Паскалю два знаменитых вопроса, первый из которых он попытался решить сам.
Вопросы были такие:
1. Сколько раз надо бросать две игральные кости, чтобы случаев выпадения сразу двух шестерок было больше половины от общего числа бросаний?
2. Как справедливо разделить поставленные на кон двумя игроками деньги, если они по каким-то причинам прекратили игру преждевременно?
Эти задачи обсуждались в переписке двух великих ученых Б.Паскаля и П.Ферма (1601-1665) и послужили поводом для первоначального введения такого важного понятия, как математическое ожидание, и попыток формулирования основных теорем сложения и произведения вероятностей.
Настоящую научную основу теории вероятностей заложил великий математик Якоб Бернулли (1654-1705). Его труд "Ars conjectandi" стал первым основательным трактатом по теории вероятностей. Он содержал общую теорию перестановок и сочетаний. А открытый им знаменитый закон больших чисел дал возможность установить связь между вероятностью какого-либо случайного события и частотой его появления, наблюдаемой непосредственно из опыта.
Дальнейшие успехи теории вероятностей связаны прежде всего с именами ученых А.Муавра (1667-1754), П.Лапласа (1749-1827), К.Гаусса (1777-1855), С.Пуассона (1781-1840) и других.
Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем Колмогоровым. В результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики.
В мире случайных явлений, хотя они и случайные, имеются закономерности. Вероятность представляет собой количественную характеристику возможности наступления некоторого случайного события. Исторически сложились различные подходы к определению вероятности. Классическое определение вероятности сформировалось в XVII в. в результате анализа азартных игр и основано на понятии равновозможности событий.
Рассмотрим испытание, в результате которого может появиться событие А. Каждый исход, при котором осуществляется событие А, называется благоприятным событию А.
Пример 9. событие А – «выпадение четного числа очков при одном бросании игральной кости». Из шести равновозможных исходов (от одного до шести очков) три исхода (2, 4, 6) являются благоприятными событию А.
Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех элементарных событий в ПГС.
Итак, вероятность события А определяется формулой
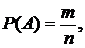 (*)
(*)
где 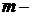 число элементарных исходов, благоприятствующих А;
число элементарных исходов, благоприятствующих А;
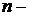 число всех возможных элементарных исходов в ПГС.
число всех возможных элементарных исходов в ПГС.
Пример 10. Вероятность появления четного числа очков при одном бросании игральной кости равна 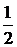 , так как число всех исходов 6, а число исходов, благоприятных событию – 3.
, так как число всех исходов 6, а число исходов, благоприятных событию – 3.
Из определения вероятности вытекают следующие свойства:
10. Вероятность достоверного события равна единице.
Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию ( 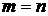 ).
).
20. Вероятность невозможного события равна нулю.
Действительно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию ( 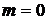 ).
).
30.Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 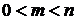 , значит,
, значит, 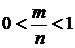 , следовательно,
, следовательно, 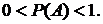 Итак, вероятность любого события удовлетворяет двойному неравенству
Итак, вероятность любого события удовлетворяет двойному неравенству 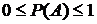 .
.
При решении задач на вычисление вероятностей возникают трудности, связанные с определением числа тех или иных исходов испытания. В таких случаях используются комбинаторные формулы, которые мы обсуждали в предыдущей теме.
Методические рекомендации. Анализ и решение задач на вычисление вероятности рассматриваемого события по формуле (*) могут быть выполнены по следующей схеме:
1. Уясните, в чем состоит испытание, рассматриваемое в задаче.
2. Установите, являются ли исходы испытаний равновозможными и несовместными.
3. Выяснив, учитывается или нет порядок расположения элементов в производимой выборке, подсчитайте по соответствующей формуле комбинаторики число всех возможных исходов испытания, т.е. число n всех элементарных событий, образующих ПГС.
4. Сформулируйте событие, вероятность которого требуется найти.
5. Подсчитайте, число m элементарных событий благоприятствующих рассматриваемому событию непосредственно, или применив соответствующие формулы комбинаторики.
6. По формуле (*) вычислите искомую вероятность.
Примеры непосредственного вычисления вероятностей.
Пример 1. В урне 10 красных и 8 синих шаров. Наугад вынимают один. Какова вероятность того, что вынут шар красного цвета?
□ Испытание – извлечение шара. Это испытание имеет 18 равновозможных и несовместных событий, образующих ПГС. Каждый исход означает выбор одного шара. Пусть событие А – «выбор красного шара». Число исходов, благоприятных событию А, равно числу красных шаров в урне – 10. Итак, 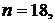
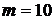 и
и 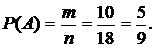 ■
■
Пример 2. В лотерее разыгрывается 1000 билетов. Из них 15 выигрывают по 50 000 руб., 25 – по 10 000 руб., 60 – по 5000 руб. Играющий приобрел один билет. Какова вероятность выиграть не менее 10 000 руб.?
□ Испытание состоит в выборе наугад одного билета из 1000. Поэтому число всех исходов (несовместных и равновозможных) равно 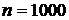 . Пусть событие А состоит в том, что участник лотереи приобрел билет, который выигрывает либо 50 000, либо 10 000 рублей. Число всех таких билетов равно
. Пусть событие А состоит в том, что участник лотереи приобрел билет, который выигрывает либо 50 000, либо 10 000 рублей. Число всех таких билетов равно 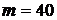 . Поэтому
. Поэтому 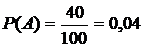 ■
■
Пример 3. Набирая номер телефона, абонент забыл последние две цифры, и набрал их наудачу. Найти вероятность того, что набраны нужные цифры: а) если известно, что эти цифры различны.
□ Пусть событие А состоит в том, что «абонент набрал две нужные цифры».
а) всего можно набрать столько пар различных цифр, сколько может быть составлено размещений без повторений из 10 цифр по две, т.е. 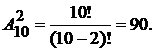 Значит, общее число всех элементарных событий, образующих ПГС, равно 90
Значит, общее число всех элементарных событий, образующих ПГС, равно 90 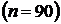 . Благоприятствует А лишь одно элементарное событие
. Благоприятствует А лишь одно элементарное событие 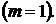 Тогда по определению вероятности
Тогда по определению вероятности 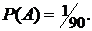 ■
■
Пример 4. Найти вероятность того, что при бросании трех игральных костей шестерка выпадет на одной (безразлично какой) кости, если на гранях двух других костей выпадут числа очков, не совпадающие между собой (и не равные 6).
□ 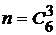 ,
, 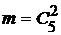 .
. 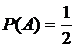 .■
.■
Пример 5. В партии из 18 деталей находятся 4 бракованных. Наугад выбирают 5 деталей. Найти вероятность того, что из этих 5 деталей две окажутся бракованными.
□ Число всех равновозможных несовместных исходов 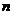 равно числу сочетаний из 18 по 5, т.е.
равно числу сочетаний из 18 по 5, т.е. 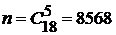 .
.
Подсчитаем число исходов  , благоприятствующих событию А. Среди 5 взятых наугад деталей должно быть 3 качественных и 2 бракованных. Число способов выборки двух бракованных деталей из 4 имеющихся бракованных равно числу сочетаний из 4 по 2:
, благоприятствующих событию А. Среди 5 взятых наугад деталей должно быть 3 качественных и 2 бракованных. Число способов выборки двух бракованных деталей из 4 имеющихся бракованных равно числу сочетаний из 4 по 2: 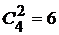 .
.
Число способов выборки трех качественных деталей из 14 имеющихся качественных равно 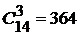 .
.
Любая группа качественных деталей может комбинироваться с любой группой бракованных деталей, поэтому общее число комбинаций  составляет
составляет 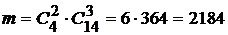 .
.
Искомая вероятность события А равна отношению числа исходов  , благоприятствующих событию, к числу
, благоприятствующих событию, к числу  всех равновозможных и несовместных событий
всех равновозможных и несовместных событий 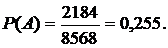 ■
■
Дифференциальное исчисление
Вопросы по теме
1. Понятие производной. Понятие дифференциала. Основные правила дифференцирования.
2. Дифференциальное исчисление нескольких переменных. Дифференциал функции.
3. Производной сложной функции.
4. Дифференциалы высших порядков.
Краткие теоретические сведения
Производнойфункции 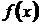 в точке
в точке 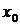 называется предел отношения приращения
называется предел отношения приращения 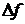 функции в этой точке к приращению
функции в этой точке к приращению 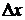 аргумента, когда последнее стремится к нулю:
аргумента, когда последнее стремится к нулю: 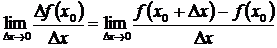 .
.
Функция 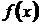 , имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой в этом промежутке.
, имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой в этом промежутке.
Для производной функции 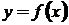 употребляются следующие обозначения:
употребляются следующие обозначения: 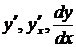 или
или 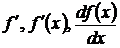 . Нахождение производной называется дифференцированием.
. Нахождение производной называется дифференцированием.
Основные правила дифференцирования
Пусть  - постоянная,
- постоянная,  - аргумент,
- аргумент, 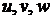 - функции от
- функции от  , имеющие производные, тогда:
, имеющие производные, тогда:
1. производная алгебраической суммы функций 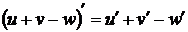 ;
;
2. производная произведения двух (трех) функций 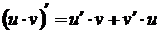 , (
, ( 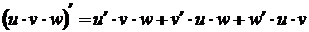 );
);
3. производная произведения константы (постоянной) на функцию
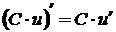 ;
;
4. производная частного (дроби)
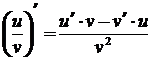 ;
; 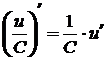 ;
; 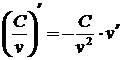 .
.
Если  есть функция от
есть функция от 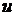 :
: 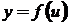 , где
, где 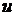 , в свою очередь, есть функция от
, в свою очередь, есть функция от  :
: 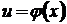 , т.е. если
, т.е. если  зависит от
зависит от  через промежуточный аргумент
через промежуточный аргумент 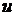 , то
, то  называется сложной функцией от
называется сложной функцией от  (функцией от функции):
(функцией от функции): 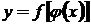 .
.
Производная от сложной функции равна произведению ее производной по промежуточному аргументу на производную этого аргумента по независимой переменной:
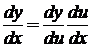 , или
, или 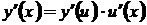 .
.
При вычислении производных необходимо помнить, что:
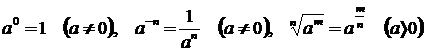
и знать правила действий со степенями и корнями: m,n – любые числа
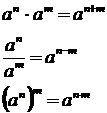
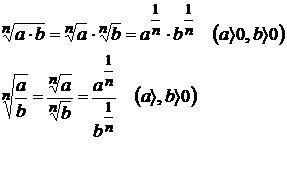
Таблица производных элементарных функций:
1 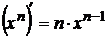 2
2 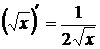 3
3 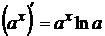 4
4 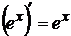
| 5 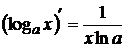 6
6 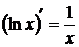 7
7 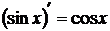 8
8 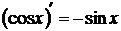
| 9 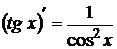 10
10 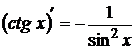 11
11 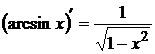
| 12 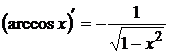 13
13 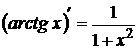 14
14 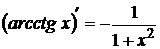
|
Примеры вычисления производной функции:
1. 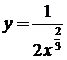 преобразуем функцию к виду
преобразуем функцию к виду 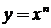 , а затем воспользуемся правилом дифференцирования (3) и формулой (1)
, а затем воспользуемся правилом дифференцирования (3) и формулой (1) 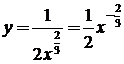 , получим
, получим 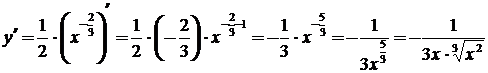
2. 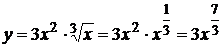
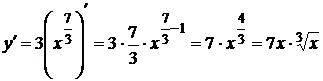
3. 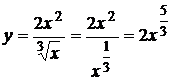
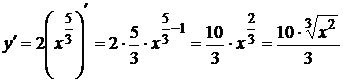
4. 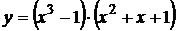
используем правило нахождения производной произведения 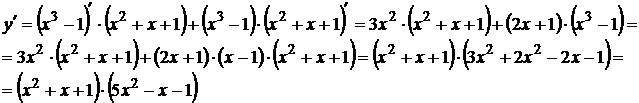
5. 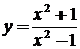 используем правило нахождения производной частного
используем правило нахождения производной частного
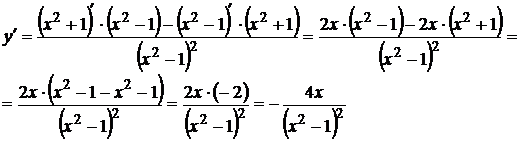
6. 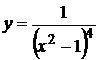
1 способ: используем частный случай нахождения производной частного
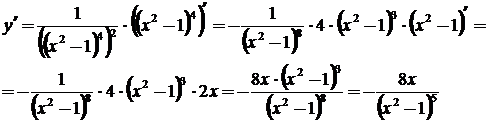
2 способ: введем, отрицательный показатель
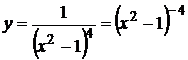
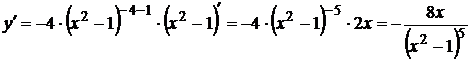
7. 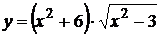 используем формулу (2), получаем:
используем формулу (2), получаем:
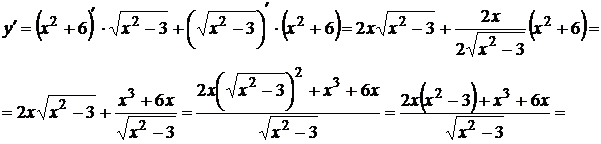
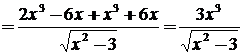
8. 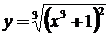 заменим кубический корень дробным показателем
заменим кубический корень дробным показателем 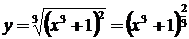
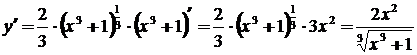
9. 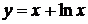
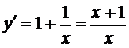
10. 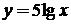
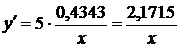
11. 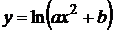
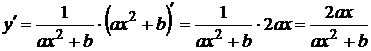
12. 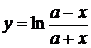 для упрощения нахождения производной предварительно прологарифмируем дробь:
для упрощения нахождения производной предварительно прологарифмируем дробь: 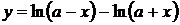
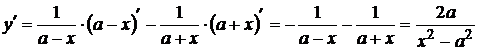
13. 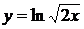 прологарифмируем дробь:
прологарифмируем дробь:
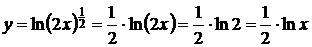
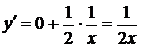
14. 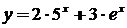
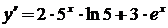
15. 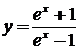
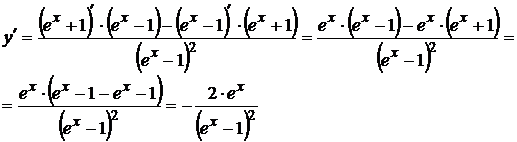
16. 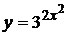 используем табличную формулу (3)
используем табличную формулу (3) 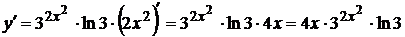
17. 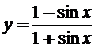
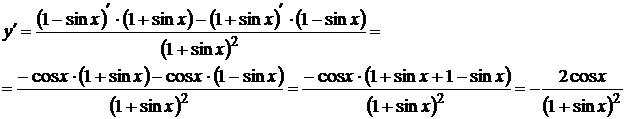
18. 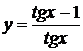
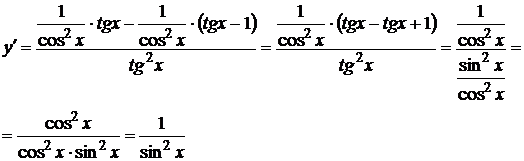
19. 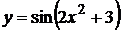
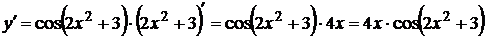
20. 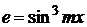
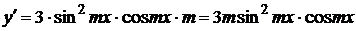 .
.
Дифференциальное исчисление нескольких переменных.
Дифференциал функции
Дифференциалом функции 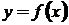 (дифференциалом I порядка) называется произведение производной этой функции
(дифференциалом I порядка) называется произведение производной этой функции 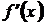 на произвольное приращение аргумента
на произвольное приращение аргумента 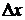 :
: 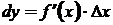 .
.
Дифференциал аргумента равен приращению аргумента 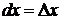 . Поэтому дифференциал функции равен произведению производной этой функции на дифференциал аргумента:
. Поэтому дифференциал функции равен произведению производной этой функции на дифференциал аргумента: 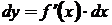 .
.
Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
Пусть 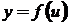 и
и 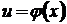 - дифференцируемые функции, которые образуют сложную функцию
- дифференцируемые функции, которые образуют сложную функцию 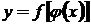 , тогда
, тогда 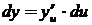 .
.
Таблица дифференциалов:
Пусть 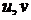 - дифференцируемые функции,
- дифференцируемые функции,  - постоянная,
- постоянная,  - любое число.
- любое число.
1. 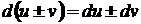 ;
;
2.  , в частности
, в частности 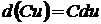 ;
;
3. 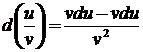 , в частности
, в частности 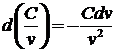 ;
;
4. 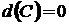 ;
;
5. 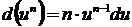 (степенная функция);
(степенная функция);
6. 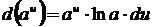 (показательная функция),
(показательная функция),
в частности 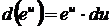 ;
;
7. 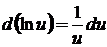 (логарифмическая функция).
(логарифмическая функция).
Примеры вычисления дифференциала функции:
1. 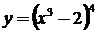 ;
; 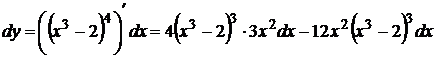
2. 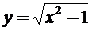 ;
; 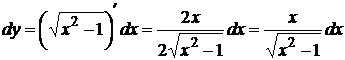
3. 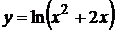 ;
; 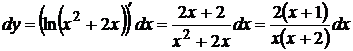
Дифференциалы высших порядков
Пусть 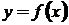 - дифференцируемая функция, ее аргумент
- дифференцируемая функция, ее аргумент  - независимая переменная. Первый дифференциал
- независимая переменная. Первый дифференциал 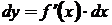 есть также функция от переменной
есть также функция от переменной  . Можно найти дифференциал от этой функции.
. Можно найти дифференциал от этой функции.
Дифференциал от дифференциала функции 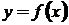 называется вторым дифференциалом (или дифференциалом II порядка), обозначается:
называется вторым дифференциалом (или дифференциалом II порядка), обозначается: 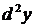 или
или 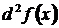 .
. 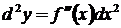 , аналогично
, аналогично 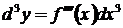 .
.
Примеры вычисления дифференциалов функции:
1. Найти дифференциал II порядка 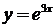 .
.
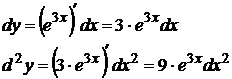
2. Найти дифференциал III порядка 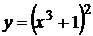 .
.
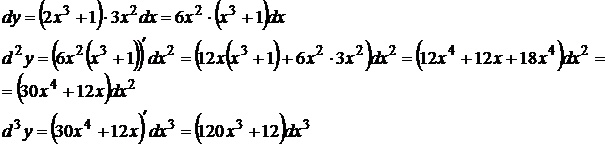
Дифференциалы функций нескольких переменных
Пусть 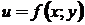 - дифференцируемая функция,
- дифференцируемая функция, 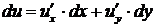 , где
, где  и
и 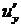 - частные производные.
- частные производные.
Для нахождения частной производной по переменной  достаточно заморозить на время «дифференцирования»
достаточно заморозить на время «дифференцирования»  и находить производную функции
и находить производную функции 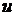 по переменной
по переменной  , на
, на  надо смотреть как на постоянную, и наоборот, при дифференцировании по
надо смотреть как на постоянную, и наоборот, при дифференцировании по  надо считать постоянной
надо считать постоянной  .
.
Примеры вычисления дифференциалов функции:
1. 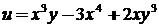
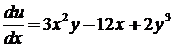
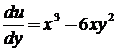
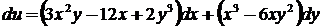
2. 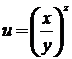
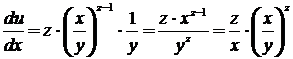
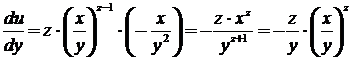
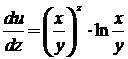
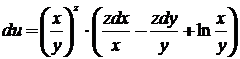
3. 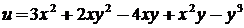
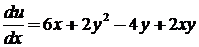
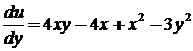
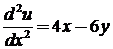
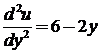
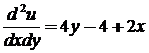
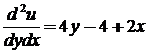
Интегральное исчисление. Неопределенный интеграл
Вопросы по теме
1. Неопределенный интеграл. Основные формулы интегрирования.
2. Непосредственное интегрирование. Интегрирование путём замены переменной. Интегрирование по частям.
3. Определенный интеграл.
Краткие теоретические сведения
Функция 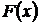 называется первообразной для функции
называется первообразной для функции 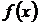 в промежутке
в промежутке 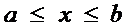 , если в любой точке этого промежутка ее производная равна
, если в любой точке этого промежутка ее производная равна 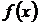 :
: 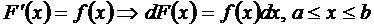 .
.
Отыскание первообразной функции по заданной ее производной 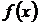 или по дифференциалу
или по дифференциалу 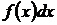 есть действие обратное дифференцированию, интегрирование.
есть действие обратное дифференцированию, интегрирование.
Совокупность первообразных для функции 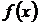 или дифференциала
или дифференциала 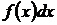 называется неопределенным интегралом и обозначается символом
называется неопределенным интегралом и обозначается символом 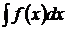 . Таким образом,
. Таким образом, 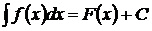 , если
, если 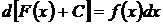 .
.
Здесь 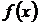 - подынтегральная функция;
- подынтегральная функция; 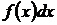 - подынтегральное выражение;
- подынтегральное выражение;  - произвольная постоянная.
- произвольная постоянная.
Основные свойства неопределенного интеграла:
1.Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная:
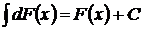 .
.
2.Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции: 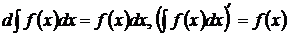 .
.
3.Неопределенный интеграл алгебраической суммы функций равен алгебраической сумме неопределенных интегралов этих функций: 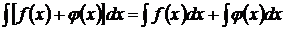 .
.
4.Постоянный множитель подынтегрального выражения можно выносить за знак неопределенного интеграла: 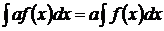
5.Если 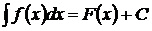 и
и 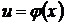 - любая известная функция, имеющая непрерывную производную, то
- любая известная функция, имеющая непрерывную производную, то 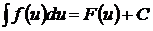 .
.
Основные формулы интегрирования (таблица простейших интегралов):
1. 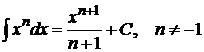
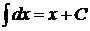 2.
2. 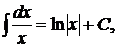 3.
3. 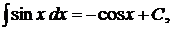 4.
4. 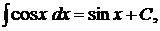 5.
5. 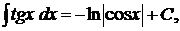 6.
6. 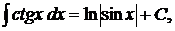 7.
7. 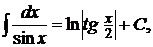 8.
8. 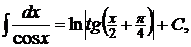 9.
9. 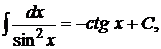 10.
10. 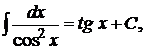 11.
11. 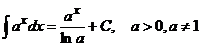 12.
12. 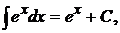
| 13. 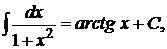 14.
14. 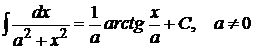 15.
15. 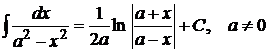 16.
16. 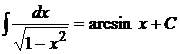 ,
17. ,
17. 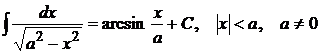 18.
18. 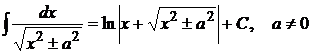 19.
19.  20.
20. 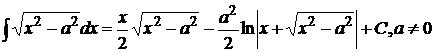 21.
21. 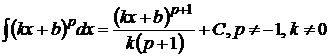 22.
22. 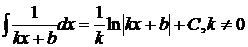 23.
23. 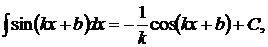 24.
24. 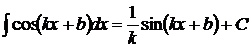 . .
|
Каждую из формул легко проверить. В результате дифференцирования правой части получается подынтегральное выражение.
Непосредственноеинтегрирование
Непосредственное интегрирование основано на прямом использовании таблицы интегралов. Здесь могут представиться следующие случаи:
1. данный интеграл находится непосредственно по соответствующему табличному интегралу;
2. данный интеграл после применения свойств 3 и 4 приводится к одному или нескольким табличным интегралам;
3. данный интеграл после элементарных тождественных преобразований над подынтегральной функцией и применения свойств 3 и 4 приводится к одному или нескольким табличным интегралам.
Примеры нахождения интегралов методом непосредственного интегрирования:
1. 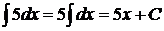 на основании свойства 4постоянный множитель 5 выносим за знак интеграла и используем формулу (1)
на основании свойства 4постоянный множитель 5 выносим за знак интеграла и используем формулу (1)
2. 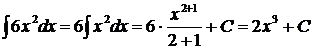 используем свойство 4 и формулу (1)
используем свойство 4 и формулу (1)
Проверка: 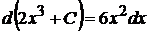 . Получили подынтегральное выражение; следовательно, интеграл найден правильно.
. Получили подынтегральное выражение; следовательно, интеграл найден правильно.
3. 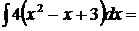 используем свойства 3и 4 и формулу (1)
используем свойства 3и 4 и формулу (1)
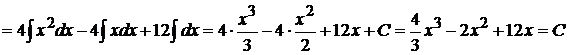 .
.
Постоянная интегрирования  равна алгебраической сумме трех постоянных интегрирования, так как каждый интеграл имеет свою произвольную постоянную
равна алгебраической сумме трех постоянных интегрирования, так как каждый интеграл имеет свою произвольную постоянную 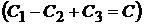 .
.
4. 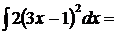 разложим квадрат разности и раскроем скобки
разложим квадрат разности и раскроем скобки
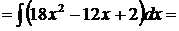 используем свойство 4 и формулу (1)
используем свойство 4 и формулу (1)
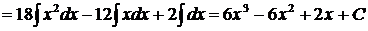 .
.
5. 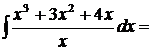 разделим каждый член числителя на знаменатель
разделим каждый член числителя на знаменатель  , далее используя свойство 4 и формулу (1)получаем:
, далее используя свойство 4 и формулу (1)получаем:

6. 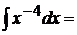 используем формулу (1)
используем формулу (1) 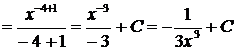
7. 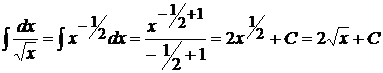
8. 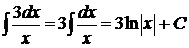 используем формулу (2)
используем формулу (2)
9. 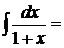 так как
так как 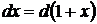 , то
, то 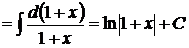 .
.
10. 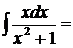 так как
так как 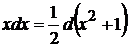 , то
, то 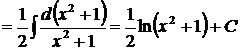 Знак абсолютной величины не пишем, так как при любом значении
Знак абсолютной величины не пишем, так как при любом значении  выражение
выражение 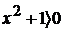 .
.
11. 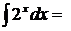 используем формулу (11) при
используем формулу (11) при 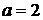 получаем
получаем 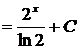 .
.
12. 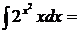 так как
так как 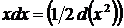 , то
, то 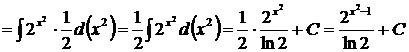 .
.
13.  так как
так как 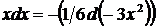 , то
, то 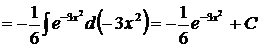 .
.
14. 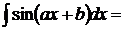 так как
так как 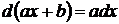 , то
, то 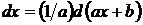
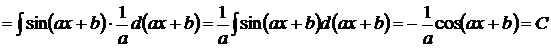 .
.
15. 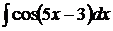
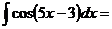 так как
так как 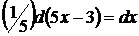 , то
, то 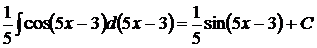 .
.
16. 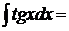 так как
так как 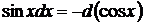 , то
, то
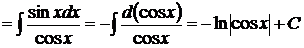 .
.
17. 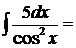
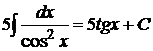 .
.
18. 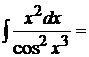 так как
так как  , то
, то 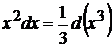 следовательно
следовательно 
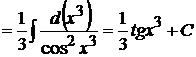 .
.
19. 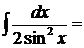
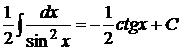 .
.
20. 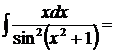 так как
так как 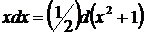 , то
, то
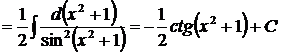 .
.
21. 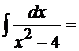
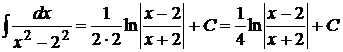 .
.
22. 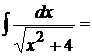
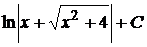 .
.
23. 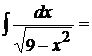
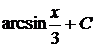 .
.
24. 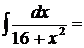
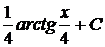 .
.
25. 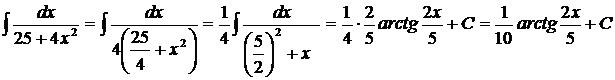
Интегрирование методом замены переменной (метод подстановки)
Сущность интегрирования методом замены переменной (способом подстановки) заключается в преобразовании интеграла 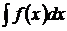 в интеграл
в интеграл 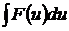 , который легко вычисляется по какой-либо из основных формул интегрирования.
, который легко вычисляется по какой-либо из основных формул интегрирования.
Для нахождения интеграла 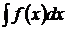 заменяем переменную
заменяем переменную  новой переменной
новой переменной 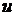 с помощью подстановки
с помощью подстановки 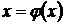 . Дифференцируя это равенство, получим
. Дифференцируя это равенство, получим 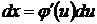 . Подставляя в подынтегральное выражение вместо
. Подставляя в подынтегральное выражение вместо  и
и 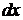 их значения, выраженные через
их значения, выраженные через 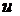 и
и 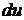 , имеем
, имеем 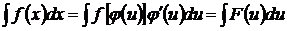 . После того как интеграл относительно новой переменной
. После того как интеграл относительно новой переменной 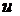 будет найден, с помощью подстановки
будет найден, с помощью подстановки 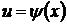 он приводит к переменной
он приводит к переменной  .
.
Примеры нахождения интегралов методом замены переменной (метод подстановки:
1. 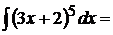
введем подстановку 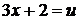 . Дифференцируя, имеем
. Дифференцируя, имеем 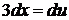 , откуда
, откуда 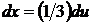 . Подставив в данный интеграл вместо
. Подставив в данный интеграл вместо 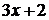 и
и 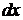 их выражения, получим
их выражения, получим 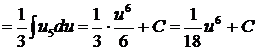 . Заменив
. Заменив 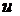 его выражением через
его выражением через  , находим
, находим 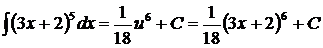 .
.
Проверка: 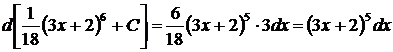 .
.
2. 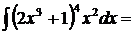
положим 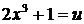 , откуда
, откуда 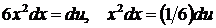 .
.
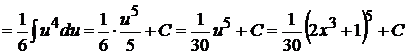 .
.
3. 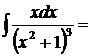 полагая
полагая 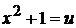 , имеем
, имеем 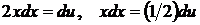 . Значит,
. Значит,
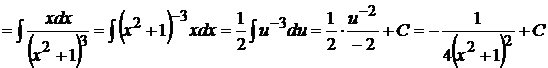 .
.
4. 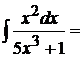 положим
положим 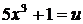 , откуда
, откуда 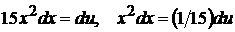 . Поэтому,
. Поэтому, 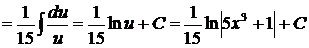 .
.
5.  положим
положим 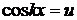 , откуда
, откуда 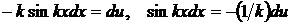 .
.
Следовательно, 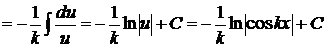 .
.
6. 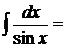 так как
так как 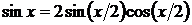 , то
, то 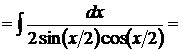 разделив и умножив знаменатель на
разделив и умножив знаменатель на 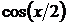 ,
,
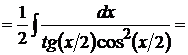 положим
положим 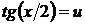 , тогда
, тогда 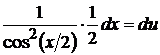 ,
,
т.е. 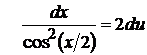 . Таким образом,
. Таким образом, 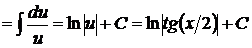 .
.
7. 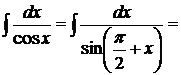 положим
положим 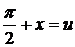 , тогда
, тогда 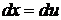 . Поэтому
. Поэтому
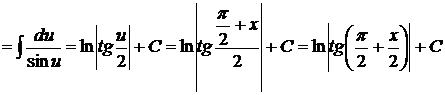 .
.
8. 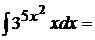 положим
положим 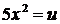 , откуда
, откуда 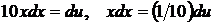 . Значит
. Значит 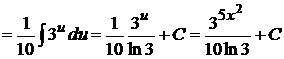 .
.
9. 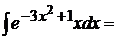 положим
положим 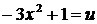 , откуда
, откуда 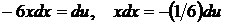 .
.
Тогда получим 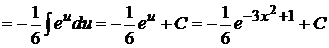 .
.
10. 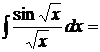 положим
положим 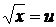 , откуда
, откуда 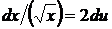 . Следовательно,
. Следовательно, 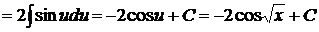 .
.
11. 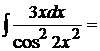 положим
положим 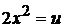 , откуда
, откуда 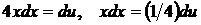 . Значит
. Значит 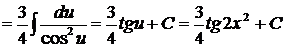 .
.
12. 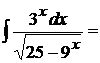 полагая
полагая 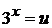 , находим
, находим 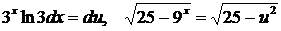 . Таким образом
. Таким образом 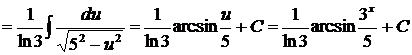 .
.
13. 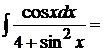 полагая
полагая 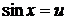 , откуда
, откуда 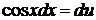 . Таким образом
. Таким образом 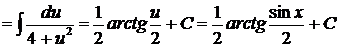 .
.
Интегрирование по частям
Интегрируя обе части равенства 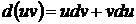 , получим
, получим 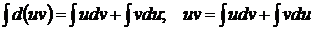 , откуда
, откуда
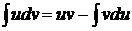 (*)
(*)
С помощью этой формулы вычисление интеграла 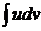 сводится к вычислению интеграла
сводится к вычислению интеграла 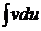 , если последний окажется проще исходного.
, если последний окажется проще исходного.
Примеры нахождения интегралов методом интегрирования по частям:
1.  положим
положим 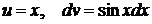 , тогда
, тогда 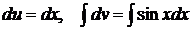 , т.е.
, т.е. 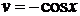 . Получаем
. Получаем 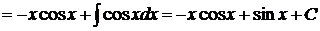 .
.
2. 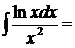 положим
положим 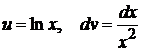 , тогда
, тогда 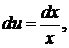
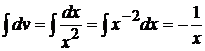 ,
, 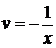 . Получим
. Получим 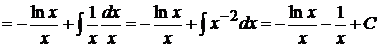 .
.
3. 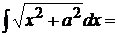 положим
положим 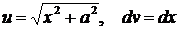 , тогда
, тогда 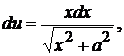
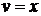 .
.
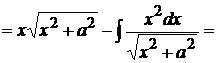 в числителе подынтегральной функции последнего интеграла прибавим и вычтем
в числителе подынтегральной функции последнего интеграла прибавим и вычтем 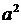 и представим этот интеграл в виде суммы двух интегралов:
и представим этот интеграл в виде суммы двух интегралов:
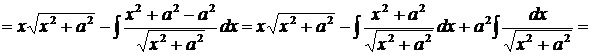
последний интеграл находим
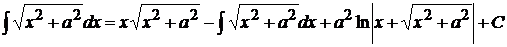 .
.
перенеся 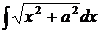 из правой части в левую, получим
из правой части в левую, получим
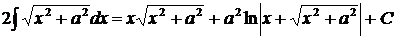 , или окончательно
, или окончательно
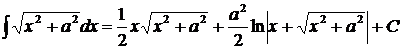 .
.
Определенный интеграл
Пусть функция 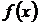 определена на отрезке
определена на отрезке 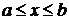 . Разобьем этот отрезок на
. Разобьем этот отрезок на  частей точками
частей точками 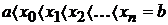 , выберем на каждом элементарном отрезке
, выберем на каждом элементарном отрезке 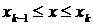 произвольную точку
произвольную точку 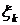 и обозначим через
и обозначим через 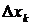 длину каждого отрезка. Интегральной суммой для функции
длину каждого отрезка. Интегральной суммой для функции 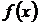 на отрезке
на отрезке 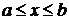 называется сумма вида
называется сумма вида 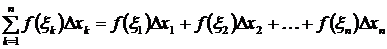 .
.
Определенным интегралом от функции 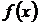 на отрезке
на отрезке 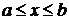 называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремиться к нулю
называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремиться к нулю 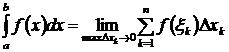 .
.
Для любой функции 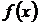 , непрерывной на отрезке
, непрерывной на отрезке 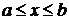 , всегда существует определенный интеграл
, всегда существует определенный интеграл 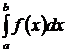 .
.
Для вычисления определенного интеграла от функции 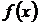 в том случае, когда можно найти соответствующий неопределенный интеграл
в том случае, когда можно найти соответствующий неопределенный интеграл 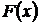 , служит формула Ньютона-Лейбница:
, служит формула Ньютона-Лейбница: 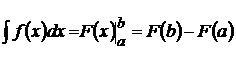 , т.е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
, т.е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
Непосредственное вычисление определенного интеграла
Примеры вычисления интегралов, используя формулу Ньютона-Лейбница:
1. 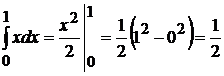 ;
;
2. 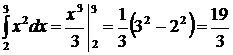 ;
;
3. 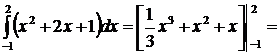
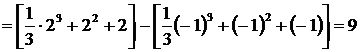
4. 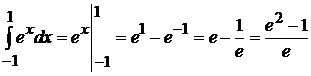 ;
;
5. 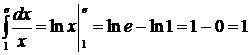 ;
;
6. 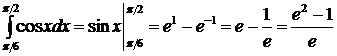 ;
;
7. 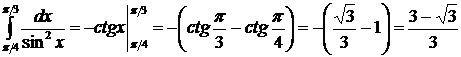 ;
;
8. 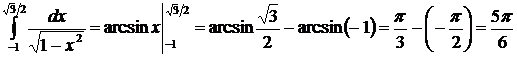 ;
;
9.  .
.
Вычисление определенного интеграла методом замены переменной
При вычислении определенного интеграла методом замены переменной (способ подстановки) определенный интеграл 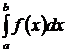 преобразуется с помощью подстановки
преобразуется с помощью подстановки 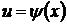 или
или 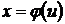 в определенный интеграл относительно новой переменной
в определенный интеграл относительно новой переменной 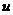 . При этом старые пределы интегрирования
. При этом старые пределы интегрирования  и
и  заменяются соответственно новыми пределами интегрирования
заменяются соответственно новыми пределами интегрирования  и
и 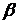 , которые находятся из исходной подстановки.
, которые находятся из исходной подстановки.
Из первой подстановки новые пределы интегрирования вычисляются непосредственно: 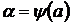 ,
, 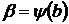 .
.
Из второй подстановки новые пределы интегрирования находятся путем решения уравнений 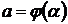 и
и 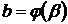 .
.
Таким образом, имеем 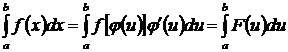 .
.
Примеры вычисления интегралов:
1. 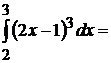 Введем новую переменную интегрирования с помощью подстановки
Введем новую переменную интегрирования с помощью подстановки 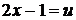 . Дифференцируя, имеем
. Дифференцируя, имеем 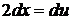 , откуда
, откуда 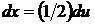 . Находим новые пределы интегрирования. Подставляя в соотношение
. Находим новые пределы интегрирования. Подставляя в соотношение 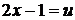 значения
значения  и
и 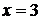 , соответственно получим
, соответственно получим 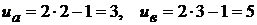 . Следовательно
. Следовательно
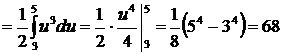 .
.
2. 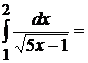 Положим
Положим 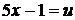 , тогда
, тогда 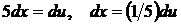 . Вычисляем новые пределы интегрирования:
. Вычисляем новые пределы интегрирования: 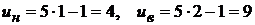 . Таким образом
. Таким образом
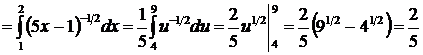 .
.
3. 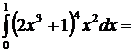 Положим
Положим 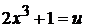 , тогда
, тогда 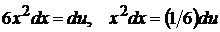 . Вычисляем новые пределы интегрирования:
. Вычисляем новые пределы интегрирования: 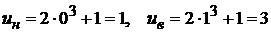 . Поэтому
. Поэтому
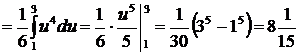 .
.
4. 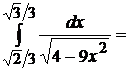 Преобразуем подкоренное выражение:
Преобразуем подкоренное выражение: 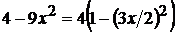 . Положим
. Положим 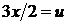 , откуда
, откуда 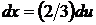 . Найдем новые пределы интегрирования:
. Найдем новые пределы интегрирования: 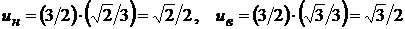 . Следовательно,
. Следовательно,
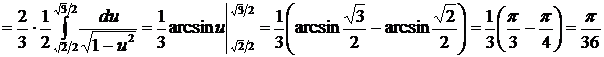
Интегрирование по частям в определенном интеграле
Если функции 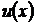 и
и 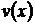 и их производные
и их производные 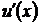 и
и 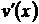 непрерывны в промежутке
непрерывны в промежутке 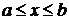 , то формула интегрирования по частям для определенного интеграла имеет вид
, то формула интегрирования по частям для определенного интеграла имеет вид 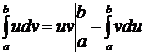 .
.
Пример вычисления интеграла:
1. 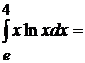 Положим
Положим 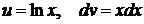 ; тогда
; тогда 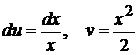 . Следовательно,
. Следовательно, 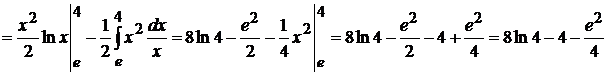 .
.
Дата добавления: 2018-02-28; просмотров: 229; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
