Кинематика. Прямолинейное движение точки
Плоская система сходящихся сил
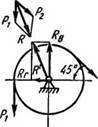
Пример 1. При подъеме груженого скипа ведущая ветвь каната подъемной машины натянута силой Р2 = 10Т и направлена под углом 45° к горизонту (см. рис.). Определить величину горизонтальной и вертикальной составляющих реакций оси шкива, пренебрегая трением в подшипниках.
 |
Решение
Равнодействующая веса поднимаемого скипа и усилия в канате
P=  =
=  =17,9Т.
=17,9Т.
Равнодействующая R и полная реакция оси R' равны по величине и направлены по одной прямой в разные стороны. Эта прямая составляет с вертикалью угол 22°30', так как угол между усилиями P1 и Р2 равен 45°, а величины P1 и Р2 одинаковы.
Величины горизонтальной и вертикальной составляющих реакций определяем из равенства:
Rг =R' sin 22°30' = 17,9 • 0,382=6,84 Т ;
RB =R' cos 22°30' =17,9∙ 0,923 = 16,5 Т.
Параллельные силы в плоскости. Момент силы. Момент пары сил.
Пример 2. На балку, шарнирно закрепленную обоими концами в крепь ствола, опирается став труб центрального водоотлива (см.рис.). Диаметр ствола D = 4200мм, вес става труб G — 420 кГ, расстояние от левой опоры до точки приложения веса става труб а = 600 мм. Определить вертикальные составляющие реакций опор.

Решение
Согласно правилам сложения двух параллельных сил

так как
b = D — a
 R2 = G-R1 ,
R2 = G-R1 ,
 =
= 
или
R1a = GD — Ga − DR1+ Rla ,
отсюда реакция левой опоры составит:
R1 =  =
=  =360 кГ
=360 кГ
реакция правой опоры
R2 = 420 — 360 = 60 кГ .
Плоская система сил
|
|
|
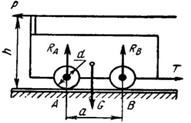
Пример 3. Загруженная вагонетка (см.рис.) весом G = 3,1 Т перемещается по рельсовому пути с помощью каната, прикрепленного к верхнему борту вагонетки на высоте h= 1250 мм. Жесткая база вагонетки а = 800 мм. Определить давление колес вагонетки на рельсы и сопротивление движению, если для перемещения вагонетки требуется усилие Р=35 кГ, а диаметр колес вагонетки d=300 мм.
Решение
Уравнения равновесия сил:
 = T-P = 0, (1)
= T-P = 0, (1)
 = Ra + RB - G = 0, (2)
= Ra + RB - G = 0, (2)
 Т
Т  + G
+ G  — RB a — Ph=0. (3)
— RB a — Ph=0. (3)
Из уравнения (1) находим:
Т = Р = 35 кГ.
Из уравнения (3) определяем:
RB = (Т  + G
+ G  - Ph)= (35
- Ph)= (35  3100
3100  - 35∙1250)
- 35∙1250)  = 1502 кГ.
= 1502 кГ.
Из уравнения (2) находим:
Ra = G — RB =3100 —1502 = 1598 кГ.
Центр тяжести и устойчивость тел
 |
Пример 4. Натяжное устройство откатки бесконечным канатом, поставленное между предохранительными упорами С и D (см.рис), имеет вес G1 = 350 к Г, размеры а = 300 мм, 6 = 200 мм, АВ = 1=500 мм. Натяжение ветвей каната уравновешено грузом 300 кГ. Определить коэффициент устойчивости .натяжного устройства.
Решение
1. Так как натяжное устройство находится в равновесии, то усилие ветвей каната находим условия
 = 0,
= 0,
т.е
 =G2 — P=0.
=G2 — P=0.
отсюда
P = G2 = 300 кГ.
2. Момент устойчивости относительно точки А создается собственным весом натяжного устройства и усилием груза
|
|
|
My =G1  + G2 b = 350
+ G2 b = 350  +300∙0,2 = 147,5 кГм.
+300∙0,2 = 147,5 кГм.
3. Опрокидывающий момент относительно той же точки создается усилием каната
М0 = Ра = 300 ∙ 0,3 = 90 кГм.
4. Коэффициент устойчивости натяжного устройства
K = 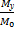
 ≈1,64.
≈1,64.
Пример 5. Подъемная машина с барабаном диаметром 5 м в заторможенном состоянии удерживает груз 12 Т. Диаметр тормозного диска машины 5,1 м. Определить тормозной момент и силу давления тормозных колодок на диск, принимая коэффициент трения равным 0,3.
Решение
Для удержания груза 12 Т тормоза подъемной машины должны создать такой тормозной момент, чтобы он был не меньше момента удерживаемого груза. Вращающий момент груза
MB = G  = 12 000
= 12 000  = 30 000 кГм.
= 30 000 кГм.
Момент пары сил трения (тормозной момент), созданный тормозными колодками,
Мт=ТD1= МB ,
отсюда сила трения
T =  =
=  = 5882 кГ.
= 5882 кГ.
Сила давления тормозных колодок на диск
N =  =
=  = 19600 кГ.
= 19600 кГ.
Кинематика. Прямолинейное движение точки
Пример 6. Подъемная установка должна поднимать груз с глубины 225 м. Определить продолжительность подъема при наибольшей скорости подъема 9 м/сек и ускорении 0,75 м/сек2.
Решение
Продолжительность ускоренного (замедленного) движения клети
t1 =  =
=  =12 сек.
=12 сек.
Путь клети при ускоренном (замедленном) движении составит:
|
|
|
S1 =  =
=  = 54 м.
= 54 м.
Такой же путь будет пройден при замедленном движении от  = 9 м/сек до
= 9 м/сек до  = 0.
= 0.
Следовательно, путь клети при равномерном движении равняется
S =H - 2S1 = 225 -2  54 = 117 м.
54 = 117 м.
Время равномерного движения клети
t2 =  =
=  = 13 сек.
= 13 сек.
Продолжительность подъема
T = 2t1 + t2 = 2∙12 + 13= 37сек.
Пример 7. Определить продолжительность одного рейса электровоза, который передвигал груженый состав со скоростью 9 км/ч, а порожний со скоростью 8 км/ч по выработкам длиной 2,1 км. Время пребывания электровоза на погрузочном пункте и в околоствольном дворе 22 мин.
Решение
Время движения груженого состава
tг =  =
=  = 840 сек.
= 840 сек.
Время движения порожнего состава
tп =  = 946 сек.
= 946 сек.
Продолжительность маневров
tм = 22∙60 =1320 сек.
Продолжительность рейса
T = tг + tп + tм = 840 + 946 +1320 = 3106 сек = 51 мин 46 сек.
Криволинейное движение точки
Пример 8. Перед подходом к закругленному участку пути радиусом 10 м вагонетка имела скорость 1,5 м/сек. В результате сопротивления на закруглении скорость вагонетки через 5 сек стала 1,1 м/сек. Определить среднюю величину полного ускорения вагонетки на закругленном участке пути.
Решение

Поступательное и вращательное движение твердого тела
|
|
|
Пример 9. Маховое колесо шахтного поршневого компрессора радиусом 1,6 м при пуске вращается равноускоренно из состояния покоя. Через 10 сек точки, лежащие на ободе маховика, имеют скорость 40 м/сек. Определить угловое ускорение и угловую скорость колеса, нормальное и касательное ускорения точек обода в конце десятой секунды.
Решение
Угловая скорость махового колеса к концу десятой секунды

Угловое ускорение махового колеса

Нормальное ускорение точек, лежащих на ободе махового колеса

Касательное ускорение точек, лежащих на ободе махового колеса,
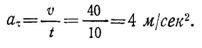
Пример 10. На валу компрессора укреплен шкив с наружным диаметром D = 250 мм. При пуске компрессора вал со шкивом начинает вращаться с постоянным ускорением ε = 15,8 сек-2. Какую линейную скорость будут иметь точки на наружной поверхности обода через 4 сек после начала вращения?
Решение
Угловая скорость шкива
ω = εt= 15,8∙4=63,2 сек-1.
Линейная скорость ремня
v= ω R=63,2∙ 0,125=7,9 м/сек.
Пример 11. Маховое колесо поршневого компрессора вращается со скоростью 375 об/мин. После отключения энергии вращение продолжалось 7 сек. Определить, сколько оборотов сделало маховое колесо за это время, вращаясь равнозамедленно.
Решение
Угловая скорость махового колеса
ω =  =
=  = 39,25 сек -1.
= 39,25 сек -1.
Угловое замедление махового колеса
ε =  =
=  = 5, 6 сек -2.
= 5, 6 сек -2.
Угол поворота колеса за время замедленного вращения
φ = ωt -  = 39,25∙7 –
= 39,25∙7 –  = 137,55 рад.
= 137,55 рад.
Число оборотов маховика за время замедленного вращения
N =  =
=  =21,9 об.
=21,9 об.
Дата добавления: 2018-02-28; просмотров: 662; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
