Максимально плоская аппроксимация
Министерство образования и науки Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра РП и РПУ
Контрольная работа по курсу
«Вопросы согласования в микроволновой технике»
Вариант 11
Факультет: РЭФ
Группа: РТз-33
Студент: Смирнов И.А.
Преподаватель: Степанов М.А.
Новосибирск 2018
Исходные данные.
Произвести расчет двухзвенной согласующей цепи комплексной нагрузки по методам Боде – Фано и Юлы.
Таблица исходных данных
| Номер варианта | fн, ГГц | fв, ГГц | f0, ГГц | 
| Rн, Ом | Lн, нГн | Cн, пФ | Rг, Ом | Вид апроксимации |
| 11 | 1,9 | 2,1 | - | - | 5 | 4,0 | 2,5 | 50 | Чебыш. |
Метод Боде – Фано.
Чебышевская аппроксимация, расчет на наилучшее качество согласования в заданной полосе частот.
1. Достроим нагрузку до резонанса на средней частоте полосы согласования.
Средняя частота заданной полосы:

Резонансная частота нагрузки:

Так как  , то достройка нагрузки до резонанса на частоте
, то достройка нагрузки до резонанса на частоте  осуществляется последовательным включением дополнительной емкости:
осуществляется последовательным включением дополнительной емкости:
 ,
,
где 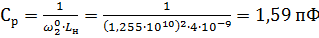 .
.
В качестве НЧ эквивалента нагрузки следует взять последовательное соединение Lэ=Lн и Rн.
2. Осуществим нормировку элементовRг, Rн и Lэотносительно Rни частоты среза низкочастотного эквивалента СЦ:

При этом:  ,
,  ,
,

Штрихами помечены нормированные элементы.
3. Определим оптимальные значения параметров аппроксимации a и bиз условий физической реализуемости СЦ и наилучшего согласования (минимального значения  ) в заданной полосе. Реактивный четырехполюсник нагрузки (рис.1) имеет простой ноль передачи при
) в заданной полосе. Реактивный четырехполюсник нагрузки (рис.1) имеет простой ноль передачи при 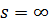 , так как при ω=∞ сопротивление индуктивности нагрузки бесконечно велико и от генератора вRн мощность не проходит. Это дает одно условие физической реализуемости
, так как при ω=∞ сопротивление индуктивности нагрузки бесконечно велико и от генератора вRн мощность не проходит. Это дает одно условие физической реализуемости 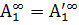 . Здесь
. Здесь  и
и 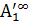 – коэффициенты разложения функций ln(1/Г2(s)) и ln(1/Г’2(s)) в ряды Лорана в нуле передачи, а Г2(s) и Г’2(s) – коэффициенты отражения в сечении подключенияRн при наличии и отсутствии СЦ соответственно (рис. 1, а и б).
– коэффициенты разложения функций ln(1/Г2(s)) и ln(1/Г’2(s)) в ряды Лорана в нуле передачи, а Г2(s) и Г’2(s) – коэффициенты отражения в сечении подключенияRн при наличии и отсутствии СЦ соответственно (рис. 1, а и б).
|
|
|

а б
Рис.1
Коэффициент 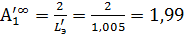 , т.к. он определяется исключительно параметрами нагрузки. А коэффициент
, т.к. он определяется исключительно параметрами нагрузки. А коэффициент  зависит только от функции Г2(s), которая для двухзвенной цепи задается в виде отношения полиномов второй степени:
зависит только от функции Г2(s), которая для двухзвенной цепи задается в виде отношения полиномов второй степени:

Коэффициенты Г2(s) выражаются через параметры аппроксимации aи b. В данном случае чебышевской аппроксимации приn=2:


Выполняя разложение функции ln(1/Г2(s)), получим условие физической реализуемости СЦ:

Вторым необходимым для нахождения неизвестных параметров аппроксимации условием является условие оптимальности СЦ по критерию минимума  . Подлежащая минимизации функция
. Подлежащая минимизации функция  . Ее оптимизацию в данном случае удобно провести методом неопределенных множителей (множителей Лагранжа). Для этого необходимо составить вспомогательную функцию:
. Ее оптимизацию в данном случае удобно провести методом неопределенных множителей (множителей Лагранжа). Для этого необходимо составить вспомогательную функцию:
|
|
|
 ,
,
а оптимальные значения aиbопределяются из уравнений:

Здесь  – неопределенный множитель. Исключая его, получим:
– неопределенный множитель. Исключая его, получим:

Эта система не решается относительно aопт и bопт. Результаты ее численного решения представлены в табл. 4.2 [1, с. 65]: aопт=1,304, bопт=0,289, 
4. По найденным параметрам аппроксимацииa и b определяем коэффициенты полиномов числителя и знаменателя Г2(s)и получившееся минимально возможное значение максимума модуля коэффициента отражения:



Подставим:

5. Далее по найденному выражению для Г2(s) определяем входное сопротивление цепи относительно точек подключения Rн (рис.2):
 , гдеci=ai+bi,di=bi-ai.
, гдеci=ai+bi,di=bi-ai.


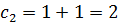
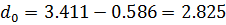


Подставим:
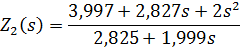
6. Затем по найденной функцииZ2(s) методом Кауэра синтезируем СЦ. Для этого дробно-рациональную функциюZ2(s) разлагаем в цепную дробь:


Получившееся расчетное сопротивление генератора  , как правило, не равно заданному. Поэтому на входе СЦ следует включить идеальный трансформатор с коэффициентом трансформации
, как правило, не равно заданному. Поэтому на входе СЦ следует включить идеальный трансформатор с коэффициентом трансформации  .
.
|
|
|
В результате синтеза приходим к низкочастотному эквиваленту СЦ (рис. 2, а).

а б
Рис. 2
7. Производим денормировку элементов и преобразуем низкочастотный эквивалент цепи в полосовую СЦ (рис. 2, б):

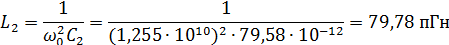
Так как 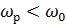 , то С1=СД, а L1=0.
, то С1=СД, а L1=0.
Метод Юлы.
Максимально плоская аппроксимация.
Расчет на максимум полосы
Дата добавления: 2018-02-28; просмотров: 322; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
