Правильные и неправильные аргументы
Умозаключение – это мысль, в ходе которой из одного или нескольких суждений выводится новое суждение.
При этом исходные суждения называются посылками, а полученное суждение – заключениемили следствием.Аристотель приводил такой пример умозаключения: «Все люди смертны» и «Сократ – человек» – посылки. «Сократ смертен» – заключение. Переход от посылок к заключению происходит по правилам вывода и законам логики.
ПРАВИЛО 1:Если посылки умозаключения истинны, то истинно и заключение.
ПРАВИЛО 2:Если умозаключение справедливо во всех случаях, то оно справедливо и в каждом частном случае. (Это правило ДЕДУКЦИИ – переход от общего к частному)
ПРАВИЛО 3:Если умозаключение справедливо в некоторых частных случаях, то оно справедливо во всех случаях. (Это правило ИНДУКЦИИ – переход от частного к общему.)
В процессе разного рода рассуждений часто возникает вопрос: как по форме (структуре) предложений, последовательность которых выражает некоторое рассуждение, определить, правильное это рассуждение или нет.
Аргументом называется совокупность предложений, про одно из которых, называемое заключением, можно сказать, что оно следует из остальных, называемых посылками (посылка, в частности, может быть и одна).
Пример 3.2. 1. «Если четырехугольник ABCD – ромб, то его диагонали взаимно перпендикулярны. Четырехугольник ABCD – ромб. Следовательно, его диагонали взаимно перпендикулярны». 2. «Если 10 делится на 3, то 100 делится на 3; 10 делится на 3; следовательно, 100 делится на 3». 3. «Если 10 – четное число, то 100 – четное число; 100 – четное число; следовательно, 10 – четное число». 4. «Если множество простых чисел конечно, то существует самое большое простое число. Наибольшего простого числа не существует. Следовательно, множество простых чисел бесконечно».
|
|
|
Из примеров видно, что посылки от заключения отделяются словом «следовательно». Сами посылки отделяются друг от друга точкой или точкой с запятой.
Выводя заключение из некоторой совокупности посылок, мы считаем, что если все посылки истинны и рассуждение правильное, то заключение также должно быть истинным. Исходя из этого, имеет место следующее определение.
Аргумент называется правильным, если из конъюнкции посылок следует заключение.
Из определения вытекает правило: Чтобы проверить, является ли аргумент правильным, достаточно: 1) формализовать все посылки и заключение; 2) составить конъюнкцию формализованных посылок; 3) проверить, следует ли формула, соответствующая заключению, из конъюнкции посылок. Если следует, то аргумент правильный, если не следует, то неправильный.
При записи аргументов в формализованном виде, используют следующий вид:  . В «числителе» записываются посылки, в «знаменателе» – заключение.
. В «числителе» записываются посылки, в «знаменателе» – заключение.
|
|
|
Пример 3.3. Какие из аргументов примера 3.2 являются правильными?
1. «Если четырехугольник ABCD – ромб, то его диагонали взаимно перпендикулярны. Четырехугольник ABCD – ромб. Следовательно, его диагонали взаимно перпендикулярны».
1) Формализуем посылки и заключение:
| Вид предложения | Предложение | Формула |

| Если четырехугольник ABCD – ромб, то его диагонали взаимно перпендикулярны. | 
|

| Четырехугольник ABCD – ромб. | 
|

| Диагонали четырехугольника взаимно перпендикулярны. | 
|
Таким образом, искомый аргумент имеет вид:  .
.
2) Составим формулу для проверки:  .
.
3) Проверим, является ли эта формула тавтологией:  . Да, является. Следовательно,
. Да, является. Следовательно, 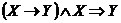 и аргумент
и аргумент  правильный.
правильный.
2. «Если 10 делится на 3, то 100 делится на 3; 10 делится на 3; следовательно, 100 делится на 3». Этот аргумент формализуется точно так же, как первый и, следовательно, является правильным.
3. «Если 10 – четное число, то 100 – четное число; 100 – четное число; следовательно, 10 – четное число».
1) Формализуем посылки и заключение:
| Вид предложения | Предложение | Формула |

| Если 10 – четное число, то 100 – четное число. | 
|

| 100 – четное число. | 
|

| 10 – четное число. | 
|
Таким образом, искомый аргумент имеет вид:  .
.
|
|
|
2) Составим формулу для проверки: 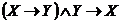 .
.
3) Проверим, является ли эта формула тавтологией: 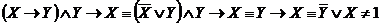 . Нет, не является. Следовательно, аргумент
. Нет, не является. Следовательно, аргумент  неправильный.
неправильный.
Надо четко понимать, что правильность аргумента сама по себе не гарантирует истинности заключения. Так, например, аргумент 2 правильный, но его заключение (100 делится на 3) ложное. Для того чтобы, рассуждая правильно, наверняка получать истинные заключения, нужно позаботиться об истинности всех без исключения посылок. Если хотя бы одна посылка правильного аргумента ложна, то заключение может оказаться как истинным, так и ложным.
Истинность всех посылок правильного аргумента является достаточным условием истинности заключения.
Если заключение истинно, то это еще не означает, что аргумент правильный. В неправильном аргументе 3 заключение истинно и истинны все посылки. Однако, истинность заключения не вытекает из истинности посылок. Рассуждая подобным образом, то есть по схеме  , можно из истинных посылок получить ложное заключение. Например, пусть X = «Углы А и В вертикальные», Y = «Углы А и В равны». Ясно, что при истинности обеих посылок («Если углы А и В вертикальные, то они равны», «Углы А и В равны»), может оказаться так, что заключение может быть ложным (углы могут быть равными и при этом не быть вертикальными, при этом первая посылка все равно остается истинной).
, можно из истинных посылок получить ложное заключение. Например, пусть X = «Углы А и В вертикальные», Y = «Углы А и В равны». Ясно, что при истинности обеих посылок («Если углы А и В вертикальные, то они равны», «Углы А и В равны»), может оказаться так, что заключение может быть ложным (углы могут быть равными и при этом не быть вертикальными, при этом первая посылка все равно остается истинной).
|
|
|
Итак, суть различия между правильными и неправильными аргументами состоит в том, что в правильном аргументе истинность всех посылок гарантирует нам истинность заключения, а в неправильном аргументе с истинными посылками заключение может быть как истинным, так и ложным.
Имеет место следующая теорема:
Теорема 4. Аргумент неправильный тогда и только тогда, когда существует такой набор значений переменных, при котором все формулы, соответствующие посылкам, принимают значение «истина», а формула, соответствующая заключению, принимает значение «ложь».
Этой теоремой удобно пользоваться при проверке правильности аргументов, особенно в тех случаях, когда посылки сложны или число их велико.
Пример 3.4. Пусть дан аргумент: «Если курс логики нетруден, то он полезен. Курс логики неинтересен или он бесполезен; Курс логики интересен. Следовательно, этот курс труден».
В формализованном виде он выглядит так:  .
.
Предполагаем, что аргумент неправильный, то есть, существует такой набор значений переменных, при котором все формулы, соответствующие посылкам, истинны, а формула, соответствующая заключению, ложна.
Все рассуждения, проистекающие из этого предположения, удобно оформлять в таблицу:
| № п/п | 1 | 0 |
| 1. | 
| |
| 2. | 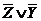
| |
| 3. | 
| |
| 4. | 
| |
| 5. |  (из 3) (из 3)
| |
| 6. |  (из 4) (из 4)
| |
| 7. |  (из 1 и 6) (из 1 и 6)
| |
| 8. |  (из 7) (из 7)
| |
| 9. | 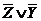 (из 5 и 8) (из 5 и 8)
|
Опишем процедуру заполнения таблицы более подробно. Первый столбик просто нумерует предложения для удобства использования. Во второй столбик заносятся истинные формулы, в третий – ложные. Первые 4 строчки составляют формулы по предположению: посылки 1-3 истинны, а заключение (4) – ложно. Остальные строчки получаются в процессе рассуждений. 5 предложение: Так как 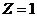 (по предположению), тогда
(по предположению), тогда  , поэтому заносим её в 3 столбик. В скобках записываем, из какого (каких) предложения (предложений) получено данное. 6 предложение: Так как
, поэтому заносим её в 3 столбик. В скобках записываем, из какого (каких) предложения (предложений) получено данное. 6 предложение: Так как  , то
, то 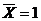 , поэтому записываем её во 2 столбик. И так далее.
, поэтому записываем её во 2 столбик. И так далее.
Таким образом, в процессе рассуждений, пришли к противоречию: по предположению, 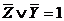 , а по предложению 9, вытекающему из предложений 5 и 8,
, а по предложению 9, вытекающему из предложений 5 и 8,  .
.
Так как в процессе рассуждений пришли к противоречию, значит, наше предположение было неверным и для данного аргумента не существует набора значений переменных, при котором все формулы, соответствующие посылкам, принимают значение «истина», а формула, соответствующая заключению, принимает значение «ложь». Таким образом, аргумент  правильный.
правильный.
Рассмотрим еще один пример. Проверим сокращенным способом правильность аргумента  .
.
| № п/п | 1 | 0 |
| 1. | 
| |
| 2. | 
| |
| 3. | 
| |
| 4. |  (из 3) (из 3)
| |
| 5. |  (из 3) (из 3)
| |
| 6. |  (из 2 и 5) (из 2 и 5)
| |
| 7. |  (из 6) (из 6)
| |
| 8. | 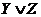 (из 5 и 7) (из 5 и 7)
| |
| 9. |  (из 1 и 8) (из 1 и 8)
|
Из таблицы видно, что нашелся такой набор значений переменных (0; 0; 0), при котором все формулы, соответствующие посылкам, принимают значение «истина», а формула, соответствующая заключению, принимает значение «ложь» и при этом никакого противоречия не возникло. Значит, аргумент  неправильный.
неправильный.
Вопросы для контроля:
1. Отношение логического следования формул алгебры высказываний и его свойства.
2. Обратная и противоположная теоремы.
3. Необходимые и достаточные условия.
4. Правильные рассуждения.
5. Способы проверки правильности рассуждений.
Дата добавления: 2018-02-28; просмотров: 1891; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
