Теоремы. Необходимые и достаточные условия
Раздел 3. Логическое следование. Применение алгебры высказываний к логико-математической практике
Логическое следование
Когда мы говорим, что одно предложение Р2 следует из другого предложения Р1, то обычно имеем в виду следующее: всякий раз, когда истинно предложение Р1, истинно и предложение Р2. В логике высказываний это означает, что для формул F1 и F2, соответствующих предложениям Р1 и Р2, не существует такого набора значений переменных, при котором F1 истинна, а F2 ложна. Например, из предложения «В пятницу я пойду в кино» следует предложение «В пятницу я пойду в кино или в театр», так как для соответствующих им формул  и
и  не возможен набор значений, при котором первая формула истинна, а вторая ложна. Соответствующая таблица истинности это показывает:
не возможен набор значений, при котором первая формула истинна, а вторая ложна. Соответствующая таблица истинности это показывает:

| 
| 
|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Говорят, что из формулы F1 следует формула F2, если  – тавтология. При этом часто употребляют запись
– тавтология. При этом часто употребляют запись  или F1 =| F2.
или F1 =| F2.
Следование, как и равносильность, является отношением между формулами. Отношение следование обладает свойствами рефлексивности и транзитивности, но не обладает свойством симметричности (вспомните определение импликации).
Для того чтобы доказать, что из формулы F1 следует формула F2, можно: 1) составить импликацию  и любым способом убедиться в том, что она является тавтологией; 2) для формул F1 и F2 составить общую таблицу истинности и убедиться в том, что всякий раз, когда формула F1 истинна, формула F2 также истинна.
и любым способом убедиться в том, что она является тавтологией; 2) для формул F1 и F2 составить общую таблицу истинности и убедиться в том, что всякий раз, когда формула F1 истинна, формула F2 также истинна.
|
|
|
Пример 3.1. Проверить, следует ли из формулы  формула
формула  .
.
1 способ. Составим импликацию  :
:  . Выясним, является ли эта импликация тавтологией с помощью равносильных преобразований:
. Выясним, является ли эта импликация тавтологией с помощью равносильных преобразований:

 .
.
Так как импликация формул F1 и F2 является тавтологией, из формулы F1 следует формула F2.
2 способ. Составим для формул F1 и F2 общую таблицу истинности:

| 
| 
| 
| 
| 
|
| 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 |
Мы видим, что всякий раз, когда формула F1 истинна, формула F2 также истинна. А значит, из формулы F1 следует формула F2.
Таким образом,  .
.
Для того чтобы доказать, что из формулы F1 не следует формула F2, достаточно найти такой набор значений переменных, входящих в эти формулы, при котором формула F1 принимает истинное значение, а формула F2 – ложное.
Определение 1. Формула B называется логическим следствием формул A1, A2, …, An, если при любых значениях входящих в них элементарных высказываний формула B принимает значение «истинно» всякий раз, когда формулы A1, A2, …, An принимают значение «истинно». Обозначается  .
.
Из определения логического следования вытекает, что:
1. Тавтология логически следует из любой формулы.
|
|
|
2. Из противоречия логически следует любая формула.
Теорема 1. Из A логически следует B тогда и только тогда, когда тавтологией является  .
.
Теорема 2.  тогда и только тогда, когда является тавтологией
тогда и только тогда, когда является тавтологией  .
.
Теорема 3. Из формул  логически следует C тогда и только тогда, когда из формул
логически следует C тогда и только тогда, когда из формул  логически следует
логически следует  .
.
Следствие 1. Из A и B логически следует C тогда и только тогда, когда тавтологией является  .
.
Следствие 2. Из формул  логически следует B тогда и только тогда, когда тавтологией является
логически следует B тогда и только тогда, когда тавтологией является  .
.
Отношение логического следования играет в математике большую роль.
Теоремы. Необходимые и достаточные условия
Теорема– это предложение, истинность которого доказывается на основе аксиом или ранее доказанных теорем. Теоремы часто формулируются в виде импликаций (следования). Импликативная структура наиболее удобна для выделения условия и заключения теоремы (того, что дано, и того, что необходимо доказать). Если импликация  выражает некоторую теорему, то основание импликации А выражает условие, а следствие В – заключение теоремы. Условие или заключение в свою очередь может не быть элементарным высказыванием, а иметь определенную логическую структуру, чаще всего конъюнктивную или дизъюнктивную. Рассмотрим примеры:
выражает некоторую теорему, то основание импликации А выражает условие, а следствие В – заключение теоремы. Условие или заключение в свою очередь может не быть элементарным высказыванием, а иметь определенную логическую структуру, чаще всего конъюнктивную или дизъюнктивную. Рассмотрим примеры:
|
|
|
1. Теорема «Если диагонали параллелограмма взаимно перпендикулярны или делят его углы пополам, то этот параллелограмм – ромб» имеет структуру  , где А = «диагонали параллелограмма взаимно перпендикулярны»; В = «(диагонали параллелограмма) делят его углы пополам»; С = «этот параллелограмм – ромб».
, где А = «диагонали параллелограмма взаимно перпендикулярны»; В = «(диагонали параллелограмма) делят его углы пополам»; С = «этот параллелограмм – ромб».
2. Теорема о средней линии трапеции («средняя линия трапеции параллельна основаниям и равна их полусумме») после соответствующей переформулировки («если четырехугольник – трапеция, то его средняя линия параллельна основаниям и равна их полусумме») имеет структуру:  , где А = «четырехугольник – трапеция»; В = «его средняя линия параллельна основаниям»; С = «(его средняя линия) равна полусумме оснований».
, где А = «четырехугольник – трапеция»; В = «его средняя линия параллельна основаниям»; С = «(его средняя линия) равна полусумме оснований».
Для каждого предложения, сформулированного в виде импликации  можно составить обратное ему предложение, противоположное и обратно-противоположное предложение. Рассмотрим их более подробно.
можно составить обратное ему предложение, противоположное и обратно-противоположное предложение. Рассмотрим их более подробно.
1. Обратное предложение  . Для всякой теоремы «если А, то В» можно сформулировать обратное ей предложение «если В, то А». При этом не для всякой теоремы, обратное ей предложение также является теоремой. Пусть, например, даны две теоремы: «Если два квадрата равны, то их площади равны»; «Если два прямоугольника равны, то их площади равны». Предложение «Если площади двух квадратов равны, то эти квадраты равны», обратное первой из этих теорем, также является теоремой. Предложение «Если площади двух прямоугольников равны, то эти прямоугольники равны», обратное второй теореме, теоремой не является, её легко опровергнуть.
. Для всякой теоремы «если А, то В» можно сформулировать обратное ей предложение «если В, то А». При этом не для всякой теоремы, обратное ей предложение также является теоремой. Пусть, например, даны две теоремы: «Если два квадрата равны, то их площади равны»; «Если два прямоугольника равны, то их площади равны». Предложение «Если площади двух квадратов равны, то эти квадраты равны», обратное первой из этих теорем, также является теоремой. Предложение «Если площади двух прямоугольников равны, то эти прямоугольники равны», обратное второй теореме, теоремой не является, её легко опровергнуть.
|
|
|
Эти примеры свидетельствуют о неравносильности предложений вида  и
и  . В неравносильности предложений такого вида можно также убедиться, сравнив таблицы истинности формул
. В неравносильности предложений такого вида можно также убедиться, сравнив таблицы истинности формул  и
и  :
:
| X | Y | 
| 
|
| 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 |
Поскольку два последних столбца в таблице не одинаковы, эквиваленция этих формул не является тавтологией, то есть они не равносильны. Более того, из таблицы видно, что одновременно с истинностью предложения вида «если А, то В», предложение вида «если В, то А» может быть как истинным, так и ложным.
Таким образом, если доказана истинность какого-либо предложения, то независимо от этого обратное ему предложение требует доказательства или опровержения.
2. Противоположные предложения  . Для всякой теоремы, сформулированной в виде импликации
. Для всякой теоремы, сформулированной в виде импликации  , можно составить противоположное предложение
, можно составить противоположное предложение  . Предложение, противоположное данной теореме, может быть также теоремой, но может ею и не быть. В этом легко убедиться, сравнив таблицы истинности формул
. Предложение, противоположное данной теореме, может быть также теоремой, но может ею и не быть. В этом легко убедиться, сравнив таблицы истинности формул  и
и 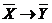 :
:
| X | Y | 
| 
| 
| 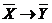
|
| 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 |
В том случае, когда предложение  истинно, предложение
истинно, предложение  может быть как истинным, так и ложным. Следовательно, предложение, противоположное доказанной теореме, в свою очередь требует доказательства или опровержения. Для наглядности рассмотрим теоремы, приведенные выше, и составим для каждой противоположное предложение. Предложение, противоположное первой теореме «Если квадраты не равны, то их площади не равны», очевидно, является теоремой. Предложение «Если прямоугольники не равны, то их площади не равны» легко опровергается примером (Прямоугольники со сторонами 3х4 и 2х6 не равны, но площадь каждого из них равна 12).
может быть как истинным, так и ложным. Следовательно, предложение, противоположное доказанной теореме, в свою очередь требует доказательства или опровержения. Для наглядности рассмотрим теоремы, приведенные выше, и составим для каждой противоположное предложение. Предложение, противоположное первой теореме «Если квадраты не равны, то их площади не равны», очевидно, является теоремой. Предложение «Если прямоугольники не равны, то их площади не равны» легко опровергается примером (Прямоугольники со сторонами 3х4 и 2х6 не равны, но площадь каждого из них равна 12).
Если условие или заключение данной теоремы представляет собой конъюнкцию или дизъюнкцию, то при составлении предложения, противоположного данной теореме, нужно учитывать соответствующий закон де Моргана. Иногда конъюнкция или дизъюнкция в формулировке теоремы присутствует неявно, «замаскированно». Поэтому, чтобы правильно сформулировать предложение, противоположное данной теореме, нужно сначала тщательно проанализировать её формулировку и выявить подразумеваемые конъюнкции или дизъюнкции (если таковые имеются). Например, в заключении теоремы «Если треугольник АВС равнобедренный, то два его угла равны» скрыта дизъюнкция: «Если в треугольнике АВС 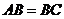 или
или  , или
, или  , то
, то 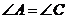 или
или  , или
, или  ». Отрицание этой дизъюнкции дает конъюнкцию: «Если в треугольнике АВС
». Отрицание этой дизъюнкции дает конъюнкцию: «Если в треугольнике АВС  и
и  , и
, и 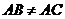 , то
, то  и
и  , и
, и  », что короче можно выразить так: «Если треугольник не равнобедренный, то никакие два его угла не равны».
», что короче можно выразить так: «Если треугольник не равнобедренный, то никакие два его угла не равны».
3. Обратно-противоположные предложения. Закон контрапозиции. Для каждой теоремы вида  можно сформулировать обратно-противоположное предложение вида
можно сформулировать обратно-противоположное предложение вида  , при этом имеет место следующая равносильность:
, при этом имеет место следующая равносильность:  , которая носит название закона контрапозиции. Согласно ему: 1) два предложения вида
, которая носит название закона контрапозиции. Согласно ему: 1) два предложения вида  и
и  одновременно истинны или одновременно ложны; 2) предложение, обратно-противоположное данной теореме, также является теоремой; 3) вместо данной теоремы можно доказывать обратно-противоположную ей теорему.
одновременно истинны или одновременно ложны; 2) предложение, обратно-противоположное данной теореме, также является теоремой; 3) вместо данной теоремы можно доказывать обратно-противоположную ей теорему.
Пусть, например, требуется доказать утверждение «Если 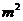 нечетно, то т нечетно». Сформулируем и докажем обратно-противоположную теорему: «Если т четно, то
нечетно, то т нечетно». Сформулируем и докажем обратно-противоположную теорему: «Если т четно, то 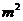 четно»; действительно, если т четно, то
четно»; действительно, если т четно, то  (р – натуральное число), откуда
(р – натуральное число), откуда  , то есть
, то есть 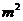 четно.
четно.
Если в равносильность  подставить Y вместо Х и Х вместо Y, то получим
подставить Y вместо Х и Х вместо Y, то получим 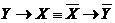 . Из этой равносильности следует: 1) предложение, обратное данному и противоположное данному одновременно истинны или одновременно ложны; 2) из двух предложений – обратного данной теореме и противоположного ей – достаточно доказать или опровергнуть только одно из них; тем самым будет доказано или опровергнуто и второе.
. Из этой равносильности следует: 1) предложение, обратное данному и противоположное данному одновременно истинны или одновременно ложны; 2) из двух предложений – обратного данной теореме и противоположного ей – достаточно доказать или опровергнуть только одно из них; тем самым будет доказано или опровергнуто и второе.
Часто в формулировках теорем используются выражения «необходимо», «достаточно» «необходимо и достаточно» (признак). Если предложение  – теорема, то A называется достаточным условием для B, а B – необходимым условием для A. Например, теорему «Если квадраты равны, то их площади равны» можно сформулировать в виде необходимого условия: «Для того чтобы квадраты были равны, необходимо, чтобы их площади были равны»; или достаточного условия: «Для того чтобы площади двух квадратов были равны, достаточно, чтобы они были равны».
– теорема, то A называется достаточным условием для B, а B – необходимым условием для A. Например, теорему «Если квадраты равны, то их площади равны» можно сформулировать в виде необходимого условия: «Для того чтобы квадраты были равны, необходимо, чтобы их площади были равны»; или достаточного условия: «Для того чтобы площади двух квадратов были равны, достаточно, чтобы они были равны».
Если вместе с  предложение
предложение  также является теоремой, то A называется необходимым и достаточным условием для B, а B – необходимым и достаточным условием для A. В логике это выражение соответствует эквиваленции, которая, как известно, представима в виде конъюнкции двух импликаций. Одна из этих импликаций выражает теорему, доказывающую необходимостьпризнака, другая выражает теорему, доказывающую достаточностьпризнака. Например, признак перпендикулярности двух плоскостей:
также является теоремой, то A называется необходимым и достаточным условием для B, а B – необходимым и достаточным условием для A. В логике это выражение соответствует эквиваленции, которая, как известно, представима в виде конъюнкции двух импликаций. Одна из этих импликаций выражает теорему, доказывающую необходимостьпризнака, другая выражает теорему, доказывающую достаточностьпризнака. Например, признак перпендикулярности двух плоскостей:
«Для того чтобы две плоскости были перпендикулярны, необходимо и достаточно, чтобы одна из них проходила через прямую, перпендикулярную к другой», может быть сформулирован и так: «Две плоскости перпендикулярны, ЕСЛИ И ТОЛЬКО ЕСЛИ одна из них проходит через прямую, перпендикулярную к другой»:  или
или  .
.
Если же  – теорема, а предложение
– теорема, а предложение  теоремой не является, то А называется достаточным, но не необходимым условием для В, а В – необходимым, но не достаточным условием для А.
теоремой не является, то А называется достаточным, но не необходимым условием для В, а В – необходимым, но не достаточным условием для А.
Дата добавления: 2018-02-28; просмотров: 886; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
