Методические указания по выполнению контрольной работы № 1

⇐ ПредыдущаяСтр 5 из 9Следующая ⇒

Решение задач требует знаний закона Ома для всей цепи и ее участков, закона Кирхгофа, методики определения эквивалентного сопротивления цепи при смешанном соединении резисторов, а также умения вычислять мощность и работу электрического тока.

Задания 1 – 20

Пример 1

Для схемы, приведенной на рис. 15, определить эквивалентное сопротивление цепи R_AB, токи в каждом резисторе и напряжение U_АВприложенное к цепи. Заданы сопротивления резисторов и ток I₄ в резисторе R₄.

Рис. 15

Решение.

Задача относится к теме «Электрические цепи постоянного тока». После усвоения условия задачи проводим поэтапное решение, предварительно обозначив стрелкой направление тока в каждом резисторе. Индекс тока должен соответствовать номеру резистора, по которому он проходит.

1. Определяем общее сопротивление разветвления R₂, R₃. Резисторы соединены параллельно, поэтому

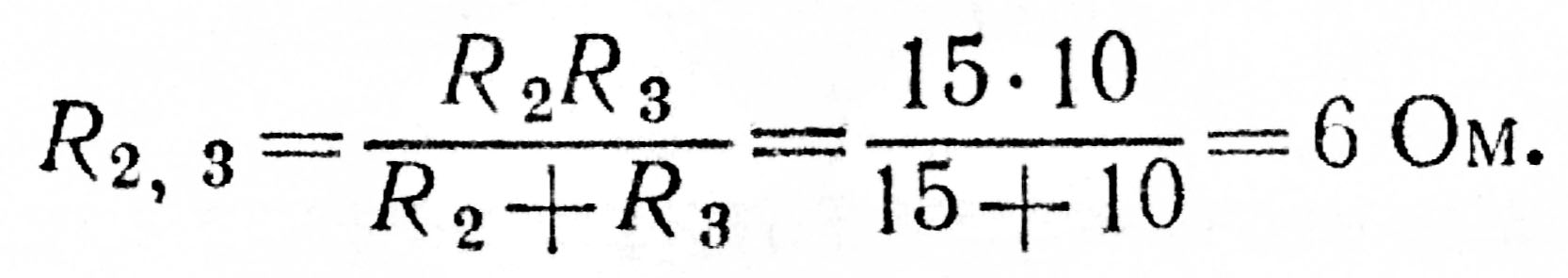
Теперь схема цепи принимает вид, показанный на рис. 15, б.

2. Резисторы R_2,3 и R₅соединены последовательно, их общее сопротивление

Соответствующая схема приведена на рис. 15 в,

3. Резисторы R_2,3,5 и R₄соединены параллельно, их общее сопротивление

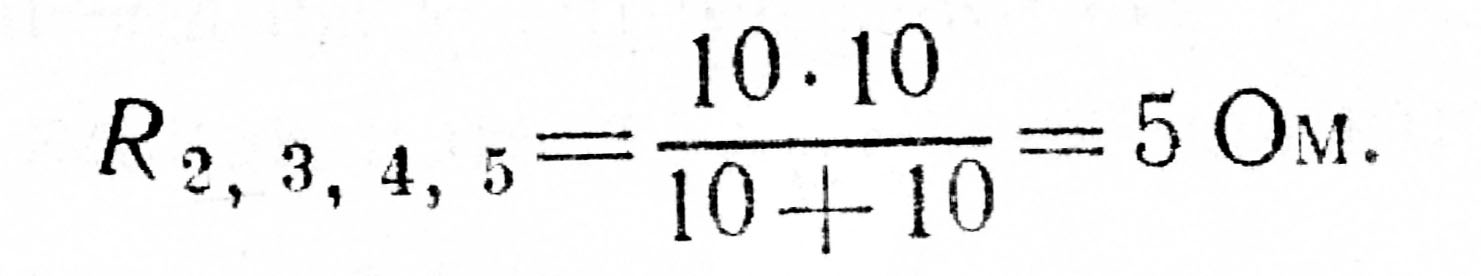
Теперь схема цепи имеет вид, приведенный на рис. 15, г.

4. Находим эквивалентное сопротивление всей цепи (рис. 15, д):

5. Зная силу тока I₄, находим напряжение на резисторе R₄ :

Это же напряжение приложено к резисторам R_2,3 + R₅ (рис. 15, б). Поэтому ток в резисторе R₅

6. Находим падение напряжения на резисторе R₅ :

Поэтому напряжение на резисторах R_2,3:

7. Определяем токи в резисторах R₂ и R₃

Применяя первый закон Кирхгофа, находим ток в резисторе R₁:

8. Вычисляем падение напряжения на резисторе R₁ :

9. Находим напряжение U_AB, приложенное ко всей цепи:

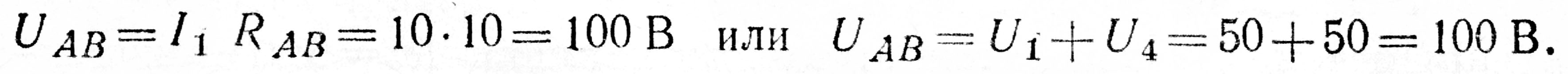
10. Мощность, потребляемая цепью:

Вт

Задания 21 – 40

Задачи относятся к неразветвленным цепям переменного тока. Перед их решением необходимо изучить материал темы «Электрические цепи переменного тока» и ознакомиться с методикой построения векторных диаграмм.

Для построения векторных диаграмм воспользуйтесь таблицей 6.

Таблица 6

Пример 2

Активное сопротивление катушки R_k = 6 Ом, индуктивное x_L=10 Ом. Последовательно с катушкой включено активное сопротивление R=2 Ом и конденсатор сопротивлением x_C=Ом (рис. 16, а). К цепи приложено напряжение U=50 В (действующее значение). Определить:

1) полное сопротивление цепи;

2) ток;

3) коэффициент мощности;

4) активную, реактивную и полную мощности;

5) напряжения на каждом сопротивлении.

Начертите в масштабе векторную диаграмму цепи.

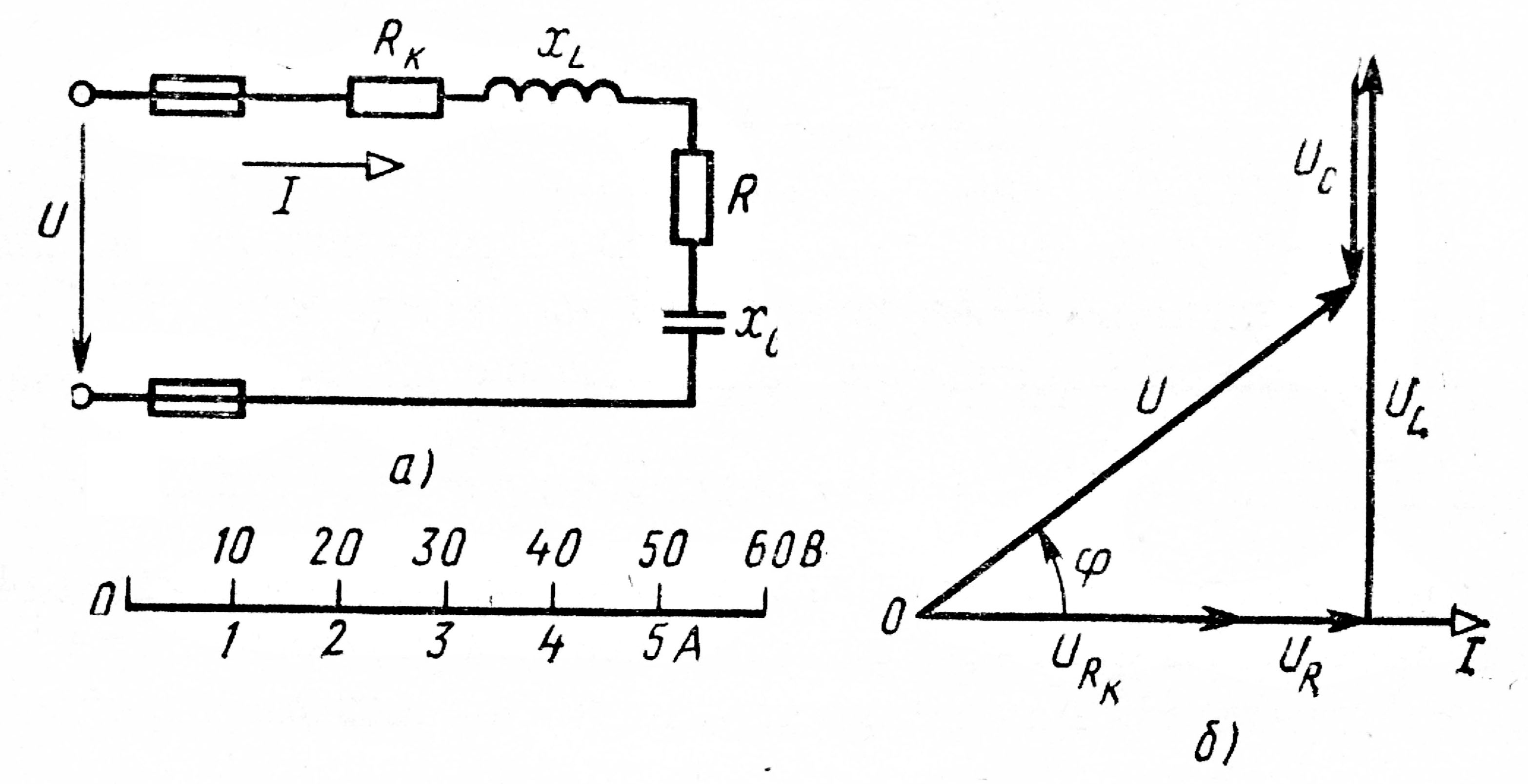
Рис. 16

Решение.

1. Определяем полное сопротивление цепи:

2. Определяем ток:

3. Определяем коэффициент мощности цепи:

по таблицам Брадиса находим φ = 36^o50’. Угол сдвига фаз φ находим по синусу во избежание потери знака угла (косинус является четной функцией).

4. Определяем активную мощность цепи:

или

Здесь

5. Определяем реактивную мощность цепи:

или

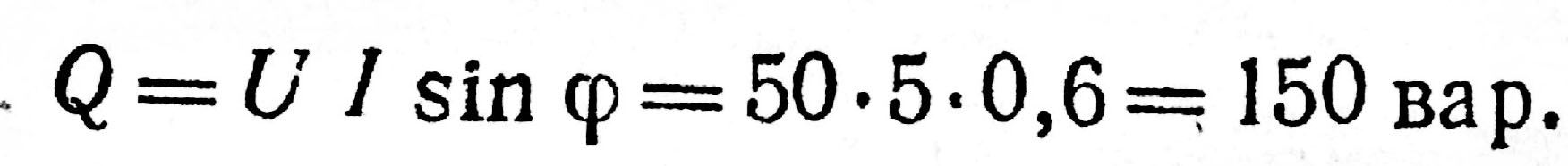
6. Определяем полную мощность цепи:

или

7. Определяем падения напряжения на сопротивлениях цепи:

Построение векторной диаграммы начинаем с выбора масштаба для тока и напряжения. Задаемся масштабом по току: в 1 см — 1,0 А и масштабом по напряжению: в 1 см — 10 В, Построение векторной диаграммы (рис. 16, б) начинаем с вектора тока, который откладываем по горизонтали в масштабе

Вдоль вектора тока откладываем векторы падений напряжения на активных сопротивлениях U_Rk и U_R:

Из конца вектора U_R откладываем в сторону опережения вектора тока на 90^o вектор падения напряжения U_Lна индуктивном сопротивлении длиной Из конца вектора U_L откладываем в сторону отставания от вектора тока на 90° вектор падения напряжения на конденсаторе U_c длиной . Геометрическая сумма векторов U_R, U_L и U_Cравна полному напряжению U, приложенному к цепи.

Задания 41 – 60

Пример 3

На рис. 3, а задана векторная диаграмма для неразветвленной цепи, токIи падения напряжений на каждом сопротивлении(U₁, U₂и т. д.). Определить характер и величину каждого сопротивления» начертить эквивалентную схему цепи, вычислить приложенное напряжение и угол сдвига фаз φ.

Рис. 17

Решение.

1. Из векторной диаграммы следует, что напряжение U₁отстает от тока на угол 90°. Следовательно, на первом участке включен конденсатор, сопротивление которого

Вектор напряжения на втором участке U₂ направлен параллельно вектору тока, т. е. совпадает с ним по фазе. Значит, на втором участке включено активное сопротивление

Вектор напряжения на третьем участке U₃ опережает вектор тока на угол 90°, что характерно для индуктивности, сопротивление которой

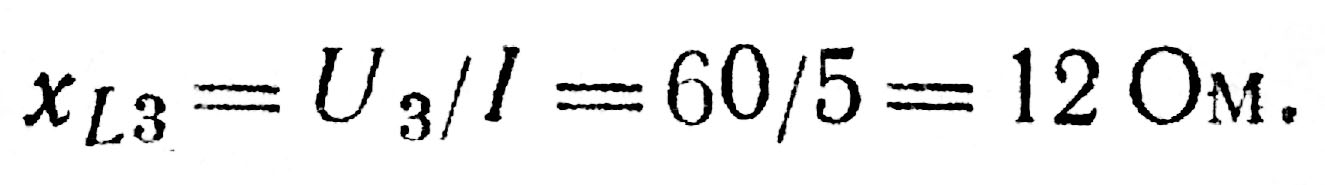
На четвертом участке включено активное сопротивление

Эквивалентная схема цепи приведена на рис. 17, б,

2.Из векторной диаграммы определяем значение приложенного напряжения и угол сдвига фаз:

Задания 61 – 70

В задачах рассматриваются основные характеристики электроизмерительных приборов: класс точности, цена деления, номинальное значение измеряемой величины и т.д.

Следует помнить, что результат измерения всегда отличается от действительного значения измеряемой величины, т. е. в процессе измерения имеет место погрешность.

Важнейшей характеристикой измерительного прибора, определяющей его точность в любой точке шкалы, является класс точности, который указывается на шкале прибора.

Каждый класс характеризуется наибольшей допустимой приведенной погрешностью, значение которой равно номеру класса и определяется по следующей формуле:

Здесь А_н - предельное значение измеряемой величины, т. е. номинальное значение шкалы прибора; ΔА_наиб - наибольшая абсолютная погрешность, т. е. наибольшая разность между показанием прибора А_и и действительным значением измеряемой величины А.

По классу точности прибора можно подсчитать наибольшую абсолютную погрешность, которую может иметь прибор в любой точке шкалы, и, следовательно, и наибольшую абсолютную погрешность при измерении какой-либо величины этим прибором:

Действительное значение измеряемой величины определяется по формуле:

Точность измерения характеризуется также наибольшей возможной относительной погрешностью:

При решении задач вместо «А» в формулы вольтметра надо подставить напряжение U, для амперметра - ток I, для ваттметра -мощность Р.

Шкала электроизмерительных приборов иногда разделена на α_н делений без указания значения этих делений в измеряемых единицах. Ценой деления (постоянной) прибора называется число электрических единиц, приходящихся на одно деление шкалы прибора.

Цена деления:

где U_н, I_н, Р_н – номинальные значения напряжения и тока приборов;

α_н – полное число делений шкалы прибора.

Чувствительность прибора – S величина, обратная постоянной прибора

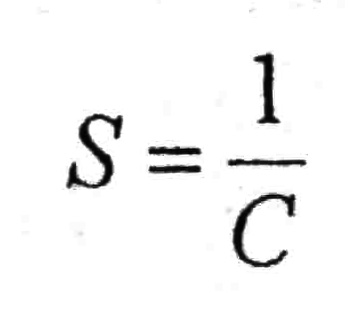
Если при измерении стрелка прибора отклонилась на α делений, то значение измеряемой величины будет:

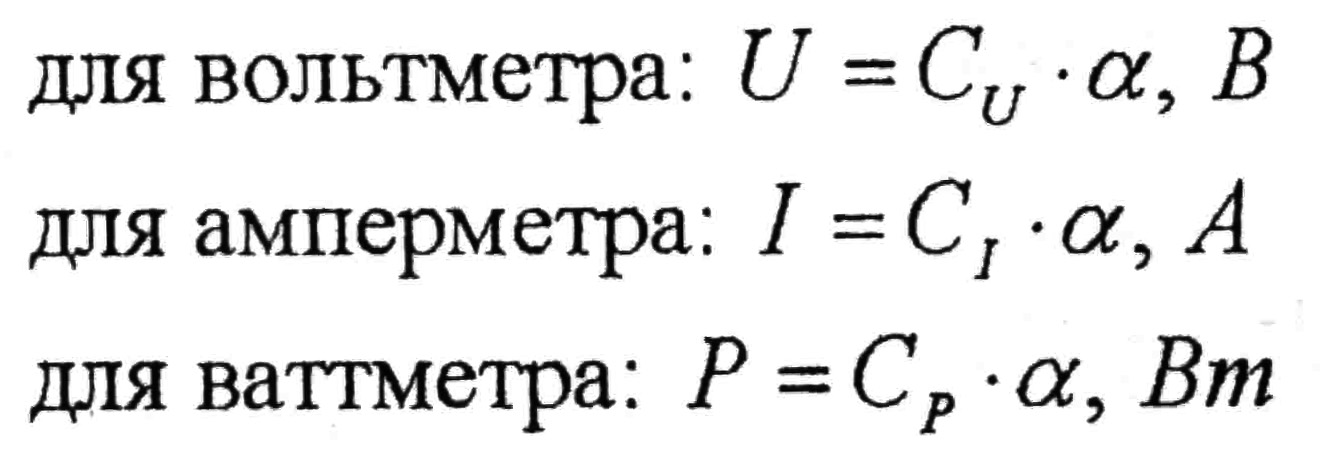
Непосредственно перед решением задач следует разобрать пример 4.

Пример 4

Вольтметр типа Э515 рассчитан на U_н=300 В, его шкала имеет α_н=150 делений. Класс точности прибора γ_д=±0,5%.

Определить постоянную C_U и чувствительность прибора S_U, а также наибольшую абсолютную погрешность ΔU_наиб. Вычислить наибольшую относительную погрешность измерения γ_нв, если стрелка прибора отклонилась на α = 120 дел. Какую при этом мощность P_U будет потреблять прибор, если его внутреннее сопротивление R_U=40 кОм.

Краткая запись условия:

Дано

Э515

U_н=300 В

α_н=150 дел.

γ_д=±0,5%.

α = 120 дел

R_U=40 кОм

Определить: C_U, S_U, ΔU_наиб. P_U .

Решение

1. Постоянная прибора и его чувствительность:

2. Наибольшая возможная абсолютная погрешность:

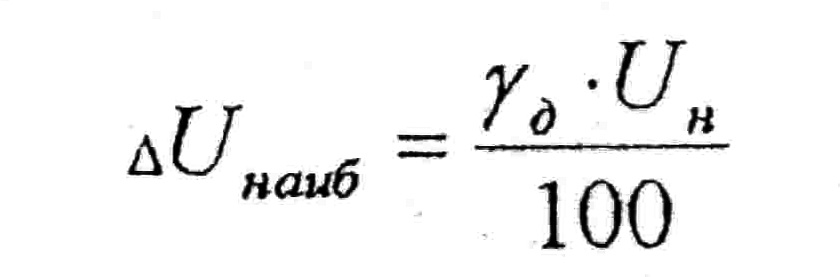
3. Измеренное значение напряжения:

4. Наибольшая возможная относительная погрешность:

5. Мощность, потребляемая вольтметром:

Задания 71 – 80

В задачах 71 – 80 рассматривается явление электромагнитной силы и явление электромагнитной индукции, принцип работы электродвигателя и электрического генератора.

Необходимо знать формулу индуктированной в проводнике ЭДС, а также правило правой руки, применяемое для определения этой ЭДС, формулу электромагнитной силы и правило левой руки для определения этой силы.

В примере 5 рассмотрен режим работы электродвигателя.

В примере 6 рассмотрен режим работы электрического генератора.

Пример 5

Прямой проводник длиной l = 0,5 м присоединен к зажимам источника питания с напряжением U = 5 В и находится в однородном магнитном поле с индукцией В = 1,4 Т, сопротивление проводника R₀ = 0,1 Ом. В результате взаимодействия с однородным магнитным полем проводник движется перпендикулярно направлению поля со скоростью υ = 5 м/с. Определить пусковой ток в проводнике, I_п, электромагнитную силу F_эм, действующую на проводник, и ток в движущемся проводнике I.

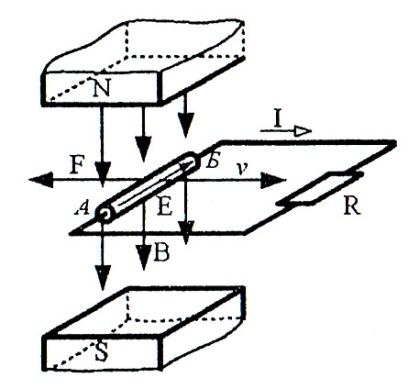
Направление ЭДС Е, тока I, и силы Fэм, показать на рис. 18.

Составить уравнение баланса мощностей в цепи.

Краткая запись условия:

Дано:

l = 0,5 м

U = 5 В

В = 1,4 Т

R₀ = 0,1 Ом

υ = 5 м/с

Определить: I_п, F_эм, I.

Составить баланс мощностей.

Рис. 18

Решение

1. Ток двигателя при пуске (υ = 0, E = 0):

2. Под воздействием электромагнитной силы проводник будет двигаться, в нем возникнет ЭДС:

3. Ток в движущемся проводнике:

Направление тока совпадает с направлением напряжения.

4. Электромагнитная сила, под действием которой проводник движется:

На. рис. 18 F_эм = F

Направление силы F_эм определено по правилу левой руки, направление движения (скорости υ) проводника совпадает с направлением силы F_эм. Направление ЭДС Е определено по правилу правой руки, оно противоположно направлению напряжения источника питания, поэтому эта ЭДС называется противоэлектродвижущей силой – противоЭДС. Направления тока I, силы F_эм (F) и противоЭДС показано на рис. 18

5. Уравнение баланса мощностей цепи имеет вид:

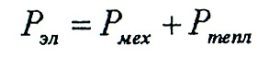
Электрическая мощность, подводимая к проводнику:

Механическая мощность, развиваемая проводником:

Потери мощности в проводнике (тепловые потери):

Уравнение баланса мощностей:

Баланс мощности сошелся.

Пример 6

В однородном магнитном поле с индукцией В = 1,25 Т перпендикулярно направлению магнитного поля движется проводник длиной l = 36 см со скоростью
υ = 16 м/c. Проводник замкнут на резистор, сопротивление которого R = 0,72 Ом, сопротивление самого проводника R₀ = 0,08 Ом.

Определить ЭДС Е, наводимую в проводнике, ток I в цепи и электромагнитную тормозную силу F_торм, действующую на проводник.

Направление ЭДС Е, тока I и силы F_торм показать на рис. 19.

Составить уравнение баланса мощностей цепи.

Краткая запись условия:

Дано:

В = 1,25 Т

l = 36 см

υ = 16 м/c

R = 0,72 Ом

R₀ = 0,08 Ом

Определить: Е, I, F_торм.

Составить баланс мощностей цепи.

Рис. 19

Решение

1. ЭДС в проводнике (согласно закону электромагнитной индукции):

2. Ток в цепи, возникший под действием ЭДС:

3. Электромагнитная сила, действующая на проводник:

Направление ЭДС Е определено по правилу правой руки. Так как в примере рассматривается режим работы генератора, то направление тока совпадает с направлением ЭДС. Направление силы F_эм, определенное по правилу левой руки, противоположно скорости υ, т.е. сила носит тормозной характер: F_эм = F_торм; она уравновешивает внешнюю механическую силу. Направления ЭДС Е, тока I, силы F_торм (F) показаны на рис. 19.

4. Уравнение баланса мощностей цепи имеет вид:

Механическая мощность:

Электрическая мощность:

Мощность тепловых потерь:

Таким образом, баланс мощности сошелся:

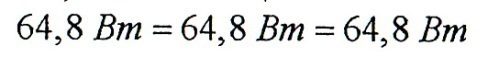
Дата добавления: 2018-02-28; просмотров: 2958; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 Следующая ⇒

Мы поможем в написании ваших работ!